6.6: Reactions of Complexes
- Page ID
- 125409
The reactions of complexes are classified into the substitution reaction of ligands, the conversion reaction of ligands, and the redox reaction of the central metal. The substitution and redox reactions in particular have been studied in detail.
(a) Ligand substitution reaction
Ligand substitution reactions of complexes
\[L_{n} MX + Y \rightarrow L_{n} MY + X \nonumber \]
are very important for the preparation of various kinds of derivatives. The detailed conditions which complexes and ligands fulfill have been studied in order to understand their stereochemistry and attain practical rates of substitution reactions. As with other types of chemical reactions, we require an understanding of both equilibrium and reaction rates.
Formation constant
The equilibrium constant of a ligand substitution reaction is called a formation or stability constant. The concept and the method of computing successive formation constants were proposed by N. Bjerrum (1941). Equilibrium constants for the replacement of a hydrated ion M by other ligands L in an aqueous solution are
| \[M + L \rightarrow ML \qquad \qquad K_{1} = \frac{[ML]}{[M][L]}$$ |
| \[ML + L \rightarrow ML_{2} \qquad \qquad K_{2} = \frac{[ML_{2}]}{[ML][L]}$$ |
| \[ML_{2} + L \rightarrow ML_{3} \qquad \qquad K_{3} = \frac{[ML_{3}]}{[ML_{2}][L]}$$ |
| …………………….. |
| \[ML_{n-1} + L \rightarrow ML_{n} \qquad \qquad K_{n} = \frac{[ML_{n}]}{[ML_{n-1}][L]}$$ |
and the overall formation constant \(beta_{n}\) is
\[\beta_{n} = \frac{[ML_{n}]}{[M][L]^{n}} = K_{1}K_{2}K_{3} \cdots K_{n} \nonumber \]
The thermodynamic stability of a substitution product becomes larger as the formation constant increases.
On the other hand, an understanding of the effect of the leaving ligand, X, and the entering ligand, Y, on the substitution rate and on the intermediate species formed are essential to elucidate the reaction chemistry of metal complexes. It is especially useful to summarize the electronic structure of the central metals, the stereochemistry of complexes, and the correlation between the parameters representing their steric properties and the reaction rate. Generally, reaction mechanisms can be classified into associative, interchange, and dissociative mechanisms according to the differences in the intermediate state (Figure \(\PageIndex{26}\)).
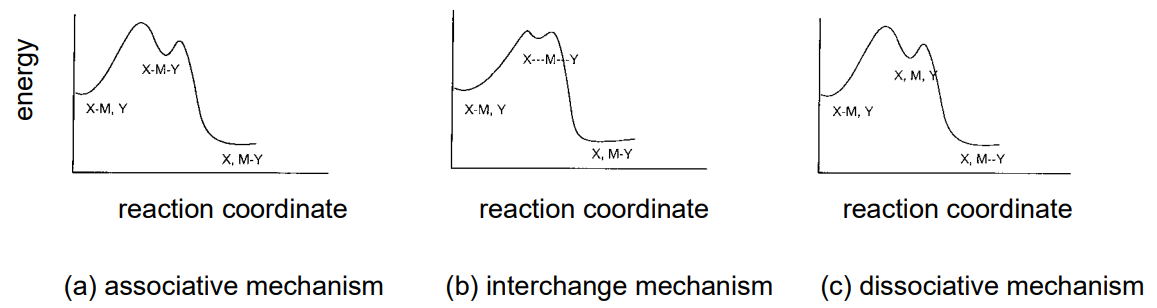
Associative mechanism
If the substitution rate of a ligand substitution of a complex is dependant upon the entering ligand, Y, coordinating to the central metal and is insensitive to the leaving ligand, X, it is presumed to take the associative mechanism which increases the coordination number. Such a substitution reaction is often seen in planar tetra-coordinate Pt(II) complexes, and the intermediate species are triangular bipyramidal penta-coordinate complexes. The reaction is first-order with respect to both the tetra-coordinate complex and Y, and is second-order as a whole. Since it is accompanied by a reduction of molecular species in the intermediate stage, thermodynamic measurements of the reaction indicate the activation entropy, \(Delta\)S, to be negative. The intermediate species in the case of the associative mechanism in hexa-coordinate complexes are hepta-coordinate complexes.
Interchange mechanism
When the life of an intermediate state is very short, the reaction proceeds by the interchange mechanism, as the coordination of Y and elimination of X are considered to occur simultaneously.
Dissociative mechanism
A substitution reaction that is highly sensitive to the identity of the leaving ligand, X, and practically insensitive to the identity of the entering ligand, Y, assumes the dissociative mechanism in which the coordination number decreases in the intermediate state. This is often observed in octahedral hexa-coordinate complexes, and the intermediate states are penta-coordinate complexes that form by the elimination of X. As the elimination is accompanied by an increase of molecular species in the intermediate stage, the entropy of activation, \(\Delta\)S, becomes positive.
The order of the rate of ligand substitution of Pt(II) complexes is H2O < Cl- < I- < PR3 < CN- for entering ligands. Which mechanism, associative or dissociative, do the substitutions take?
- Answer
-
Since they are dependent on the entering ligands, the associative mechanism is more likely.
Trans effect
In square-planar tetra-coordinate complexes typically of Pt(II), the ligand trans to the leaving ligand X governs the substitution rate. This is called the trans effect. The substitution rate increases as the σ donor or π acceptor ability of the trans ligand becomes larger in the order of NH3 < Cl- < Br- < I- < NCS- < PR3 < CN- < CO. An analogous effect may also be seen in octahedral hexa-coordinate complexes, although the effect is usually relatively small.
The H2O exchange rate in aqua ions
Inert, intermediate, and labile are classification of the exchange rate proposed by H. Taube (1952). The exchange rate of aqua ions (ions coordinated by water molecules) of main-group and transition metals differ greatly depending upon the identity of the metal species. Since the rate of water ligand exchange is well correlated withthe exchange rates of other ligands, it is useful for general comparison of the exchange rates in the complexes of different metal ions. For alkali and alkaline earth metals, the exchange rates are very high (105 - 109 s-1), and the complexes of these metals are classified as labile. As the dissociative mechanism is generally found in these cases, ions with smaller ionicity and of larger size attract water ligands less and their exchange rates becomes higher. In Group 12 metal ions Zn2+, Cd2+, Hg2+, Group 13 metal ions Al3+, Ga3+, In3+ and Group 3 metal ions Sc3+, Y3+, rapid water ligand exchange takes place by a dissociative mechanism.
On the other hand, the exchange rates of M (II) ions in d block transition metal ions is medium (10 - 104 s-1), and that of M (III) ions are lower still. The rates of d3 Cr3+ and d6 Co3+ are notably slow (10-1 - 10-9 s-1), and their complexes are termed inert. There has been a great deal of study of ligand-exchange reactions. The exchange rates are smaller the larger the ligand field stabilization energy. Therefore, the ligand-exchange rates of 4d and 5d transition metal complexes are generally slow.
Test tube experiments
Easy chemical or biological reactions performed in test tubes are sometimes called test tube experiments. Solutions in test tubes are mixed at room temperature in air and the mixture is shaken to observe a color change or formation of precipitates and the results of the reactions are speculated on. University professors occasionally attempt these sorts of experiments. Although easy, these simple experiments show only the effects of visible light absorption and solubility. However, since even great discoveries can be born from such experiments, they should not be dismissed.
H. Taube wrote that he found a hint of the inner-sphere electron transfer mechanism from test tube experiments. He mixed Cr2+(aq) and I2 in a test tube in order to clarify the oxidation of Cr2+(aq) and observed the change of color to the one characteristic of [Cr(H2O)6]3+ via green. The green color is due to [(H2O)5CrI]2+ which is unstable and changes to [Cr(H2O)6]3+ + I-. He assumed that this was due to the formation of a Cr-I bond before Cr(II) was oxidized by I2. Subsequently, he performed another test tube experiment using [(NH3)5CoCl]2+ as an oxidant and found that Cr2+(aq) was converted into [Cr(H2O)6]3+ via green [(H2O)5CrCl]2+. This reaction established the inner-sphere electron transfer mechanism in which a Co-Cl-Cr bridge forms between Co3+ and Cr2+ and led to the Nobel Prize in a later year.
(b) Redox reactions
The oxidation number of the central metal in a transition-metal compound can vary in a few steps from low to high. Namely, the oxidation state of a compound is changeable by redox reactions. As a consequence of this, the bond distance and the bond angle between the metal and coordinating elements, or between metals, change, and at times the whole structure of a complex can be distorted remarkably or the compound may even decompose.
The reactions of a metal compound with various reducing or oxidizing agents are also very important from the viewpoint of synthetic chemistry. Especially, reduction reactions are used in the preparation of organometallic compounds, such as metal carbonyls or cluster compounds.
Meanwhile, the study of electron transfer between complexes, especially the redox reactions of transition metal complexes, has developed. Taube won the Nobel Prize (1983) for the study of electron transfer reactions in transition metal complexes, classifying such reactions into two mechanisms. The mechanism of electron transfer in which a bridging ligand is shared between two metals is called the inner-sphere mechanism, and the one involving a direct transfer of electrons between two metals without a bridging ligand is called the outer-sphere mechanism.
Inner-sphere mechanism
When [CoCl(NH3)5]2+ is reduced by [Cr(OH2)6]2+, an intermediate complex, [(NH3)5Co-Cl-Cr(OH2)5]4+, is formed in which the chlorine atom forms a bridge between cobalt and chromium. As a result of an electron transfer from chromium to cobalt through chlorine, [Co(NH3)5Cl]+ , in which cobalt is reduced from a trivalent to a divalent oxidation state and [Cr(OH2)6]3+, in which chromium is oxidized from a divalent to a trivalent oxidation state, are formed. This kind of reaction is a redox reaction via the inner-sphere mechanism. The anions other than halogens suitable for such bridge formation are SCN-, N3-, CN-, etc.
Outer-sphere mechanism
When [Fe(phen)3]3+ (phen is orthophenanthroline) is reduced by [Fe(CN)6]4-, no ligand bridge forms between the metals and an electron moves from the HOMO of Fe(II) to the LUMO of Fe(III) in a very short and direct contact between the two complexes. As the result of the electron transfer, [Fe(phen)3]2+ and [Fe(CN)6]3- form. This kind of reaction is a redox one via the outer-sphere mechanism, and is characteristic of a complex system that has a very slow ligand substitution rate compared with the speed of electron transfer, especially in systems that have the same ligands but different oxidation-numbers, for example, [Fe(CN)6]3- - [Fe(CN)6]4- has a high rate of electron transfer. R. A. Marcus won the Nobel Prize (1992) for his study of this outer-sphere electron transfer mechanism.
6.1
Which cavity, either the octahedral or tetrahedral one, in an array of oxygen atoms do Fe2+ ions tend to occupy in iron oxide Fe3O4 containing both Fe2+ and Fe3+ ions?
6.2
Describe a method of preparing trans-[PtCl(Et)(PEt3)2].
6.3
Propose mononuclear and dinuclear metal complexes containing cyclopentadienyl and carbonyl ligands that satisfy the 18-electron rule.
6.4
Devise a method of selective syntheses of cis-[PtCl2(NH3)2] and trans-[PtCl2(NH3)2] using the trans effect.
6.5
How can it be proven that the reduction reaction of [CoCl(NH3)5]2+ by [Cr(OH2)6]2+ proceeds by the inner-sphere electron transfer mechanism?


