2.2: Constructing Molecular Orbitals from Atomic Orbitals
- Page ID
- 183297
Molecular orbital theory involves solving (approximately) the Schrödinger equation for the electrons in a molecule. To review from Chapter 1, this is a differential equation in which the first and second terms on the right represent the kinetic and potential energies:
\[E \psi = -\frac{\hbar^{2}}{2\mu} \nabla^{2} \psi + V \psi\]
While the Schrödinger equation can be solved analytically for the hydrogen atom, the potential energy function V becomes more complicated - and the equation can then only be solved numerically - when there are many (mutually repulsive) electrons in a molecule. So as a first approximation we will assume that the s, p, d, f, etc. orbitals of the atoms that make up the molecule are good solutions to the Schrödinger equation. We can then allow these wavefunctions to interfere constructively and destructively as we bring the atoms together to make bonds. In this way, we use the atomic orbitals (AO) as our basis for constructing MO's.
LCAO-MO = linear combination of atomic orbitals. In physics, this is called this the tight binding approximation.
We have actually seen linear combinations of atomic orbitals before when we constructed hybrid orbitals in Chapter 1. The basic rules we developed for hybridization also apply here: orbitals are added with scalar coefficients (c) in such a way that the resulting orbitals are orthogonal and normalized. The difference is that in the MO case, the atomic orbitals come from different atoms.
The linear combination of atomic orbitals always gives back the same number of molecular orbitals. So if we start with two atomic orbitals (e.g., an s and a pz orbital as shown in Fig. \(\PageIndex{1}\)), we end up with two molecular orbitals. When atomic orbitals add in phase, we get constructive interference and a lower energy orbital. When they add out of phase, we get a node and the resulting orbital has higher energy. The lower energy MOs are bonding and higher energy MOs are antibonding.
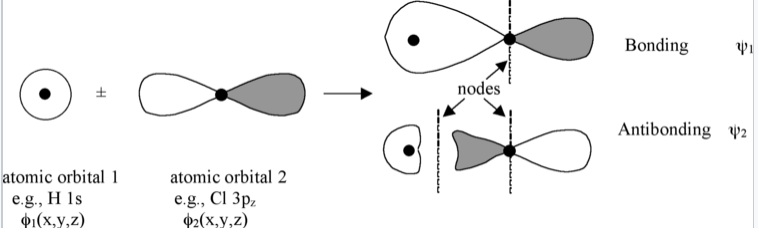
Molecular orbitals are also called wavefunctions (ψ), because they are solutions to the Schrödinger equation for the molecule. The atomic orbitals (also called basis functions) are labeled as φ's, for example, φ1s and φ3pz or simply as φ1and φ2.
In principle, we need to solve the Schrödinger equation for all the orbitals in a molecule, and then fill them up with pairs of electrons as we do for the orbitals in atoms. In practice we are really interested only in the MOs that derive from the valence orbitals of the constituent atoms, because these are the orbitals that are involved in bonding. We are especially interested in the frontier orbitals, i.e., the highest occupied molecular orbital (the HOMO) and the lowest unoccupied molecular orbital (the LUMO). Filled orbitals that are much lower in energy (i.e., core orbitals) do not contribute to bonding, and empty orbitals at higher energy likewise do not contribute. Those orbitals are however important in photochemistry and spectroscopy, which involve electronic transitions from occupied to empty orbitals. The fluorescent dyes that stain the cells shown in Fig. \(\PageIndex{2}\) absorb light by promoting electrons in the HOMO to empty MOs and give off light when the electrons drop back down to their original energy levels.
As an example of the LCAO-MO approach we can construct two MO's (ψ1 and ψ2) of the HCl molecule from two AO's φ1and φ2 (Fig. 2.1.1). To make these two linear combinations, we write:
\[\Psi_{1}=c_{1}\varphi_{1} + c_{2}\varphi_{2}\]
and
\[\Psi_{2}=c_{1}\varphi_{1} - c_{2}\varphi_{2}\]
The coefficients c1 and c2 will be equal (or nearly so) when the two AOs from which they are constructed are the same, e.g., when two hydrogen 1s orbitals combine to make bonding and antibonding MOs in H2. They will be unequal when there is an energy difference between the AOs, for example when a hydrogen 1s orbital and a chlorine 3p orbital combine to make a polar H-Cl bond.
Nodes:
The wavefunctions φ and ψ are amplitudes that are related to the probability of finding the electron at some point in space. They have lobes with (+) or (-) signs, which we indicate by shading or color. Wherever the wavefunction changes sign we have a node. As you can see in Fig. \(\PageIndex{1}\), nodes in MOs result from destructive interference of (+) and (-) wavefunctions. Generally, the more nodes, the higher the energy of the orbital.
In the example above we have drawn a simplified picture of the Cl 3pz orbital and the resulting MOs, leaving out the radial node. Recall that 2p orbitals have no radial nodes, 3p orbitals have one, as illustrated in Fig. \(\PageIndex{3}\). 4p orbitals have two radial nodes, and so on. The MOs we make by combining the AOs have these nodes too.

Normalization:
We square the wave functions to get probabilities, which are always positve or zero. So if an electron is in orbital φ1, the probability of finding it at point xyz is the square[1] of φ1(x,y,z). The total probability does not change when we combine AOs to make MOs, so for the simple case of combining φ1 and φ2 to make ψ1and ψ2,
\[\Psi_{1}^{2} + \Psi_{2}^{2} = \varphi_{1}^{2} + \varphi_{2}^{2}\]
Overlap integral:
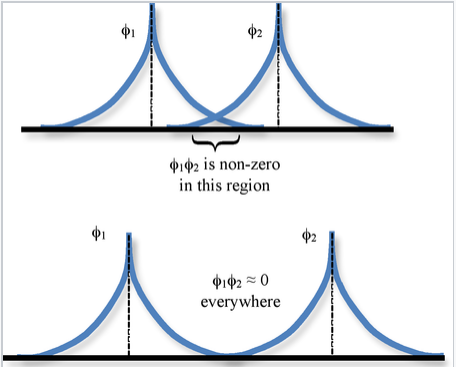
The spatial overlap between two atomic orbitals φ1 and φ2 is described by the overlap integral S,
\[S_{12} = \int \varphi_{1} * \varphi_{2} d\tau \]
where the integration is over all space \(d\tau = dx dy dz\).
Energies of bonding and antibonding MOs:
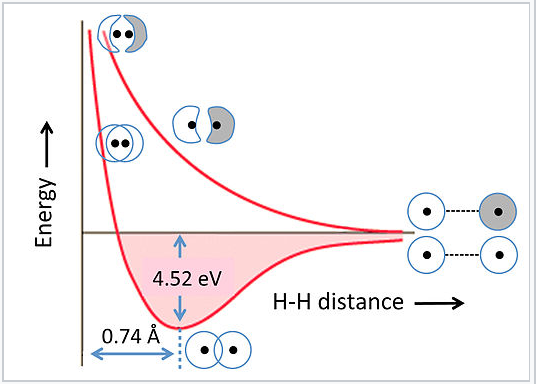
The energies of bonding and antibonding orbitals depend strongly on the distance between atoms. This is illustrated in Fig. 2.1.5 for the hydrogen molecule, H2. At very long distances, there is essentially no difference in energy between the in-phase and out-of-phase combinations of H 1s orbitals. As they get closer, the in-phase (bonding) combination drops in energy because electrons are shared between the two positively charged nuclei. The energy reaches a minimum at the equilibrium bond distance (0.74 Å) and then rises again as the nuclei get closer together. The antibonding combination has a node between the nuclei so its energy rises continuously as the atoms are brought together.
At the equilibrium bond distance, the energies of the bonding and antibonding molecular orbitals (ψ1, ψ2) are lower and higher, respectively, than the energies of the atomic basis orbitals φ1 and φ2. This is shown in Fig. \(\PageIndex{6}\) for the MO’s of the H2 molecule.
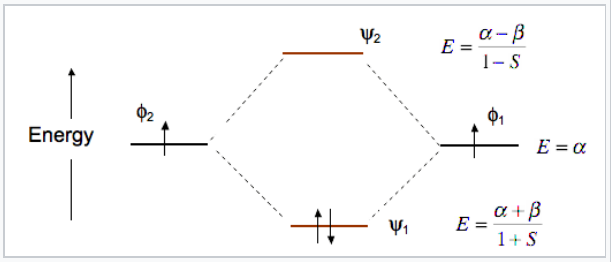
The energy of an electron in one of the atomic orbitals is α, the Coulomb integral.
\[\alpha = \int \varphi_{1} H \varphi_{1}d\tau\]
where H is the Hamiltonian operator. Essentially, α represents the ionization energy of an electron in atomic orbital φ1 or φ2.
The energy difference between an electron in the AO’s and the MO’s is determined by the exchange integral β,
\[\beta = \int \varphi_{1}H\varphi_{2}d\tau\]
β is an important quantity, because it tells us about the bonding energy of the molecule, and also the difference in energy between bonding and antibonding orbitals. Calculating β is not straightforward for multi-electron molecules because we cannot solve the Schrödinger equation analytically for the wavefunctions. We can however make some approximations to calculate the energies and wavefunctions numerically. In the Hückel approximation, which can be used to obtain approximate solutions for π molecular orbitals in organic molecules, we simplify the math by taking S=0 and setting H=0 for any p-orbitals that are not adjacent to each other. The extended Hückel method,[2] developed by Roald Hoffmann, and other semi-empirical methods can be used to rapidly obtain relative orbital energies, approximate wavefunctions, and degeneracies of molecular orbitals for a wide variety of molecules and extended solids. More sophisticated ab initio methods are now readily available in software packages and can be used to compute accurate orbital energies for molecules and solids.
We can get the coefficients c1 and c2 for the hydrogen molecule by applying the normalization criterion:
\[\Phi_{1} = (\varphi_{1} + \varphi_{2})/(\sqrt{2(1+S)}) \textrm{(bonding orbital)}\]
and
\[\Phi_{2} = (\varphi_{1} - \varphi_{2})/(\sqrt{2(1-S)}) \textrm{(antibonding orbital)}\]
In the case where S≈0, we can eliminate the 1-S terms and both coefficients become 1/√2
Note that the bonding orbital in the MO diagram of H2 is stabilized by an energy β/1+S and the antibonding orbital is destabilized by β/1-S. That is, the antibonding orbital goes up in energy more than the bonding orbital goes down. This means that H2 (ψ12ψ20) is energetically more stable than two H atoms, but He2 with four electrons (ψ12ψ22) is unstable relative to two He atoms.
Bond order: In any MO diagram, the bond order can be calculated as ½ ( # of bonding electrons - # of antibonding electrons). For H2 the bond order is 1, and for He2the bond order is zero.
Heteronuclear case (e.g., HCl) - Polar bonds
Here we introduce an electronegativity difference between the two atoms making the chemical bond. The energy of an electron in the H 1s orbital is higher (it is easier to ionize) than the electron in the chlorine 3pz orbital. This results in a larger energy difference between the resulting molecular orbitals ψ1 and ψ2, as shown in Fig. \(\PageIndex{7}\). The bigger the electronegativity difference between atomic orbitals (the larger Δα is) the more “φ2 character” the bonding orbital has, i.e., the more it resembles the Cl 3pz orbital in this case. This is consistent with the idea that H-Cl has a polar single bond: the two electrons reside in a bonding molecular orbital that is primarily localized on the Cl atom.
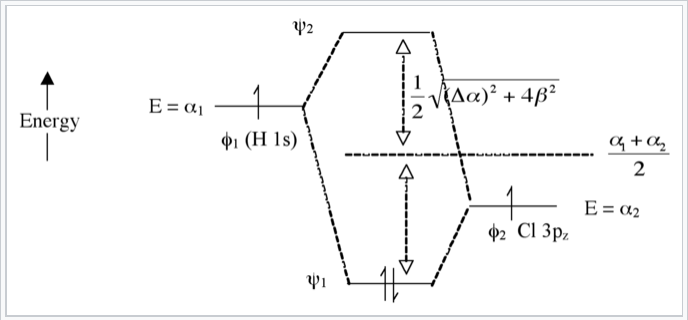
The antibonding orbital (empty) has more H-character. The bond order is again 1 because there are two electrons in the bonding orbital and none in the antibonding orbital.
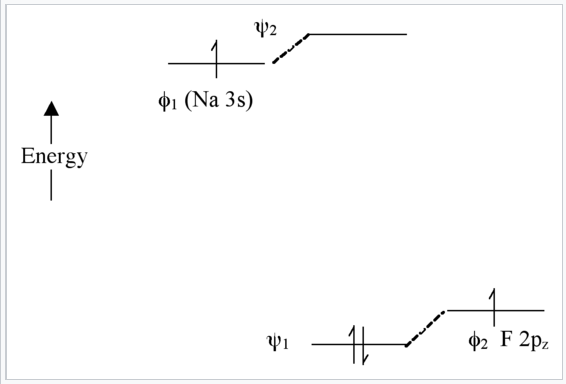
Extreme case - Ionic bonding (NaF): very large Δα
In this case, there is not much mixing between the AO’s because their energies are far apart (Fig. \(\PageIndex{8}\)). The two bonding electrons are localized on the F atom , so we can write the molecule as Na+F-. Note that if we were to excite an electron from ψ1 to ψ2 using light, the resulting electronic configuration would be (ψ11ψ21) and we would have Na0F0. This is called a charge transfer transition.
Summary of molecular orbital theory so far:
• Add and subtract AO wavefunctions to make MOs. Two AOs → two MOs. More generally, the total number of MOs equals the number of AO basis orbitals.
• We showed the simplest case (only two basis orbitals). More accurate calculations use a much larger basis set (more AOs) and solve for the matrix of c’s that gives the lowest total energy, using mathematically friendly approximations of the potential energy function that is part of the Hamiltonian operator H.
• More nodes → higher energy MO
• Bond order = ½ ( # of bonding electrons - # of antibonding electrons)
• Bond polarity emerges in the MO picture as orbital “character.”
• AOs that are far apart in energy do not interact much when they combine to make MOs.


