7.2: Work Hardening, Alloying, and Annealing
- Page ID
- 183333
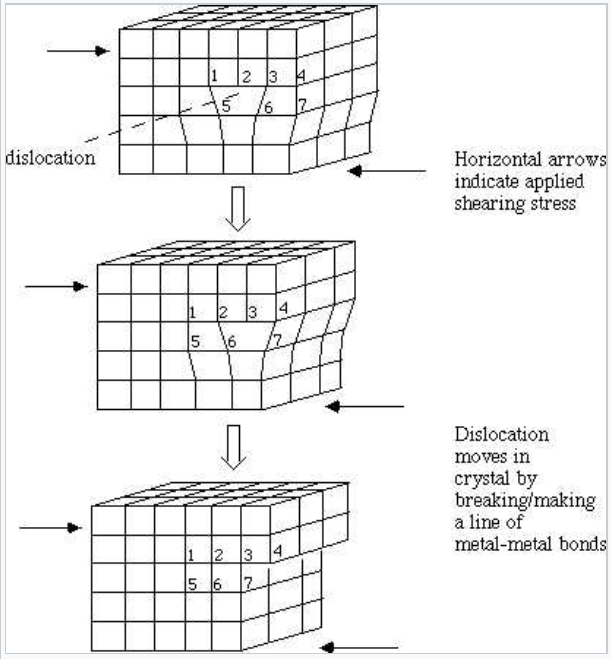
One of the questions we would like to ask is, why are the yield stresses of normal (polycrystalline) metal samples so much lower (by a factor of 1000) than they are in perfect single crystals? The answer has to do with the motion of dislocations. Consider the picture below, which shows planes of metal atoms near a dislocation (the individual atoms are numbered to help you see which bonds are broken and which are formed). The arrows indicate force applied under shear stress. Notice how the dislocation moves by breaking/making metal-metal bonds.
The key point here is that we can induce plastic deformation (shear) by breaking only one line of metal-metal bonds at a time along the dislocation line. This involves far less force than breaking an entire plane of bonds, as we would need to do to shear a perfect crystal. In a given polycrystalline sample, there are many dislocation lines that run perpendicular to all possible shear directions, so their motion can be used to "tear" the metal apart. Turbine rotors on large jets are made of very expensive single crystal nickel-titanium alloys, so that these shearing deformations can be avoided.[1]
 |
We can see that motion of dislocations is basically bad news if we want a metal to be strong and hard (e.g., if we want a structural material, or a knife that can hold a decent edge). There are several ways we can overcome (to some extent) this problem:
1. Use single crystals and anneal out all the dislocations (expensive - especially with large items like turbine blades, and impossible with very large items like airplane wings or bridges).
2. Work hardening of the metal - this moves all dislocations to grain boundaries (the dislocation essentially becomes part of the grain boundary). Since a grain boundary is a planar defect, it is much less responsive to stress than a line defect.
3. Introduce impurity atoms (that is alloying elements) or impurity phases that "pin" the motion of defects. An impurity atom stops the motion because it is a different size, or makes stronger bonds, than the other metal atoms; the line defect has a hard time moving away from rows of such atoms. An impurity phase (like Fe3C in iron) makes extra grain boundaries that can stop the motion of defects. This effect is analogous to the graphite fibers in fiber-reinforced cross-linked polymers (used, e.g., in tennis rackets) that stop the propagation of cracks.
A simple illustration of work hardening can be done with a piece of copper wire. When struck many times with a hammer, the copper wire becomes stiffer, and it is possible to hang a weight from it. Dislocations move to the crystal grain boundaries during work hardening, effectively halting their motion and at the same time making the individual crystal grains smaller. Because the crystal grains are now smaller, the amount of grain boundary area has increased, and with it the free energy of the material. Annealing reverses the process by lowering the free energy. When the wire is annealed in a flame (heated so that atoms can move and rearrange), the crystal grains grow, and the dislocations reappear. The copper again becomes ductile, and bends easily. Cold-working (work hardening) of metals is important for strengthening structural materials (e.g., iron beams) and for making brittle, hard edges (this is why blacksmiths hammer on knives and swords when they are making them. If you have ever watched them, they do the same thing to horseshoes, when they cool down, to make them stiff).
|
Blacksmith, 1606 |



