11.1: Galvanic Cells

Skills to Develop

• To understand the basics of voltaic cells
• To connect voltage from a voltaic cell to underlying REDOX chemistry

In any electrochemical process, electrons flow from one chemical substance to another, driven by an oxidation–reduction (redox) reaction. A redox reaction occurs when electrons are transferred from a substance that is oxidized to one that is being reduced. The reductant is the substance that loses electrons and is oxidized in the process; the oxidant is the species that gains electrons and is reduced in the process. The associated potential energy is determined by the potential difference between the valence electrons in atoms of different elements.

Because it is impossible to have a reduction without an oxidation and vice versa, a redox reaction can be described as two half-reactions, one representing the oxidation process and one the reduction process. For the reaction of zinc with bromine, the overall chemical reaction is as follows:

\[Zn_{(s)} + Br_{2(aq)} \rightarrow Zn^{2+}_{(aq)} + 2Br^−_{(aq)} \label{20.3.1}\]

The half-reactions are as follows:

reduction half-reaction:

\[Br_{2(aq)} + 2e^− \rightarrow 2Br^−_{(aq)} \label{20.3.2}\]

oxidation half-reaction:

\[Zn_{(s)} \rightarrow Zn^{2+}_{(aq)} + 2e^− \label{20.3.3}\]

Each half-reaction is written to show what is actually occurring in the system; Zn is the reductant in this reaction (it loses electrons), and Br₂ is the oxidant (it gains electrons). Adding the two half-reactions gives the overall chemical reaction (Equation \(\PageIndex{1}\)). A redox reaction is balanced when the number of electrons lost by the reductant equals the number of electrons gained by the oxidant. Like any balanced chemical equation, the overall process is electrically neutral; that is, the net charge is the same on both sides of the equation.

In any redox reaction, the number of electrons lost by the reductant equals the number of electrons gained by the oxidant.

In most of our discussions of chemical reactions, we have assumed that the reactants are in intimate physical contact with one another. Acid–base reactions, for example, are usually carried out with the acid and the base dispersed in a single phase, such as a liquid solution. With redox reactions, however, it is possible to physically separate the oxidation and reduction half-reactions in space, as long as there is a complete circuit, including an external electrical connection, such as a wire, between the two half-reactions. As the reaction progresses, the electrons flow from the reductant to the oxidant over this electrical connection, producing an electric current that can be used to do work. An apparatus that is used to generate electricity from a spontaneous redox reaction or, conversely, that uses electricity to drive a nonspontaneous redox reaction is called an electrochemical cell.

There are two types of electrochemical cells: galvanic cells and electrolytic cells. Galvanic cells are named for the Italian physicist and physician Luigi Galvani (1737–1798), who observed that dissected frog leg muscles twitched when a small electric shock was applied, demonstrating the electrical nature of nerve impulses. A galvanic (voltaic) cell uses the energy released during a spontaneous redox reaction (ΔG < 0) to generate electricity. This type of electrochemical cell is often called a voltaic cell after its inventor, the Italian physicist Alessandro Volta (1745–1827). In contrast, an electrolytic cell consumes electrical energy from an external source, using it to cause a nonspontaneous redox reaction to occur (ΔG > 0). Both types contain two electrodes, which are solid metals connected to an external circuit that provides an electrical connection between the two parts of the system (Figure \(\PageIndex{1}\)). The oxidation half-reaction occurs at one electrode (the anode), and the reduction half-reaction occurs at the other (the cathode). When the circuit is closed, electrons flow from the anode to the cathode. The electrodes are also connected by an electrolyte, an ionic substance or solution that allows ions to transfer between the electrode compartments, thereby maintaining the system’s electrical neutrality. In this section, we focus on reactions that occur in galvanic cells.

Figure \(\PageIndex{1}\): Electrochemical Cells. A galvanic cell (left) transforms the energy released by a spontaneous redox reaction into electrical energy that can be used to perform work. The oxidative and reductive half-reactions usually occur in separate compartments that are connected by an external electrical circuit; in addition, a second connection that allows ions to flow between the compartments (shown here as a vertical dashed line to represent a porous barrier) is necessary to maintain electrical neutrality. The potential difference between the electrodes (voltage) causes electrons to flow from the reductant to the oxidant through the external circuit, generating an electric current. In an electrolytic cell (right), an external source of electrical energy is used to generate a potential difference between the electrodes that forces electrons to flow, driving a nonspontaneous redox reaction; only a single compartment is employed in most applications. In both kinds of electrochemical cells, the anode is the electrode at which the oxidation half-reaction occurs, and the cathode is the electrode at which the reduction half-reaction occurs.

Voltaic (Galvanic) Cells

To illustrate the basic principles of a galvanic cell, let’s consider the reaction of metallic zinc with cupric ion (Cu²⁺) to give copper metal and Zn²⁺ ion. The balanced chemical equation is as follows:

\[Zn_{(s)} + Cu^{2+}_{(aq)} \rightarrow Zn^{2+}_{(aq)} + Cu_{(s)} \label{20.3.4}\]

We can cause this reaction to occur by inserting a zinc rod into an aqueous solution of copper(II) sulfate. As the reaction proceeds, the zinc rod dissolves, and a mass of metallic copper forms. These changes occur spontaneously, but all the energy released is in the form of heat rather than in a form that can be used to do work.

Figure \(\PageIndex{2}\): The Reaction of Metallic Zinc with Aqueous Copper(II) Ions in a Single Compartment. When a zinc rod is inserted into a beaker that contains an aqueous solution of copper(II) sulfate, a spontaneous redox reaction occurs: the zinc electrode dissolves to give Zn²⁺(aq) ions, while Cu²⁺(aq) ions are simultaneously reduced to metallic copper. The reaction occurs so rapidly that the copper is deposited as very fine particles that appear black, rather than the usual reddish color of copper.

This same reaction can be carried out using the galvanic cell illustrated in Figure \(\PageIndex{3a}\). To assemble the cell, a copper strip is inserted into a beaker that contains a 1 M solution of Cu²⁺ ions, and a zinc strip is inserted into a different beaker that contains a 1 M solution of Zn²⁺ ions. The two metal strips, which serve as electrodes, are connected by a wire, and the compartments are connected by a salt bridge, a U-shaped tube inserted into both solutions that contains a concentrated liquid or gelled electrolyte. The ions in the salt bridge are selected so that they do not interfere with the electrochemical reaction by being oxidized or reduced themselves or by forming a precipitate or complex; commonly used cations and anions are Na⁺ or K⁺ and NO₃⁻ or SO₄²⁻, respectively. (The ions in the salt bridge do not have to be the same as those in the redox couple in either compartment.) When the circuit is closed, a spontaneous reaction occurs: zinc metal is oxidized to Zn²⁺ ions at the zinc electrode (the anode), and Cu²⁺ ions are reduced to Cu metal at the copper electrode (the cathode). As the reaction progresses, the zinc strip dissolves, and the concentration of Zn²⁺ ions in the Zn²⁺ solution increases; simultaneously, the copper strip gains mass, and the concentration of Cu²⁺ ions in the Cu²⁺ solution decreases (Figure \(\PageIndex{3b}\)). Thus we have carried out the same reaction as we did using a single beaker, but this time the oxidative and reductive half-reactions are physically separated from each other. The electrons that are released at the anode flow through the wire, producing an electric current. Galvanic cells therefore transform chemical energy into electrical energy that can then be used to do work.

Figure \(\PageIndex{3}\): The Reaction of Metallic Zinc with Aqueous Copper(II) Ions in a Galvanic Cell. (a) A galvanic cell can be constructed by inserting a copper strip into a beaker that contains an aqueous 1 M solution of Cu²⁺ ions and a zinc strip into a different beaker that contains an aqueous 1 M solution of Zn²⁺ ions. The two metal strips are connected by a wire that allows electricity to flow, and the beakers are connected by a salt bridge. When the switch is closed to complete the circuit, the zinc electrode (the anode) is spontaneously oxidized to Zn²⁺ ions in the left compartment, while Cu²⁺ ions are simultaneously reduced to copper metal at the copper electrode (the cathode). (b) As the reaction progresses, the Zn anode loses mass as it dissolves to give Zn²⁺(aq) ions, while the Cu cathode gains mass as Cu²⁺(aq) ions are reduced to copper metal that is deposited on the cathode.

The electrolyte in the salt bridge serves two purposes: it completes the circuit by carrying electrical charge and maintains electrical neutrality in both solutions by allowing ions to migrate between them. The identity of the salt in a salt bridge is unimportant, as long as the component ions do not react or undergo a redox reaction under the operating conditions of the cell. Without such a connection, the total positive charge in the Zn²⁺ solution would increase as the zinc metal dissolves, and the total positive charge in the Cu²⁺ solution would decrease. The salt bridge allows charges to be neutralized by a flow of anions into the Zn²⁺ solution and a flow of cations into the Cu²⁺ solution. In the absence of a salt bridge or some other similar connection, the reaction would rapidly cease because electrical neutrality could not be maintained.

A voltmeter can be used to measure the difference in electrical potential between the two compartments. Opening the switch that connects the wires to the anode and the cathode prevents a current from flowing, so no chemical reaction occurs. With the switch closed, however, the external circuit is closed, and an electric current can flow from the anode to the cathode. The potential (E_cell) of the cell, measured in volts, is the difference in electrical potential between the two half-reactions and is related to the energy needed to move a charged particle in an electric field. In the cell we have described, the voltmeter indicates a potential of 1.10 V (Figure \(\PageIndex{3a}\)). Because electrons from the oxidation half-reaction are released at the anode, the anode in a galvanic cell is negatively charged. The cathode, which attracts electrons, is positively charged.

Not all electrodes undergo a chemical transformation during a redox reaction. The electrode can be made from an inert, highly conducting metal such as platinum to prevent it from reacting during a redox process, where it does not appear in the overall electrochemical reaction. This phenomenon is illustrated in Example \(\PageIndex{1}\).

A galvanic (voltaic) cell converts the energy released by a spontaneous chemical reaction to electrical energy. An electrolytic cell consumes electrical energy from an external source to drive a nonspontaneous chemical reaction.

Example \(\PageIndex{1}\)

A chemist has constructed a galvanic cell consisting of two beakers. One beaker contains a strip of tin immersed in aqueous sulfuric acid, and the other contains a platinum electrode immersed in aqueous nitric acid. The two solutions are connected by a salt bridge, and the electrodes are connected by a wire. Current begins to flow, and bubbles of a gas appear at the platinum electrode. The spontaneous redox reaction that occurs is described by the following balanced chemical equation:

\[3Sn_{(s)} + 2NO^-_{3(aq)} + 8H^+_{(aq)} \rightarrow 3Sn^{2+}_{(aq)} + 2NO_{(g)} + 4H_2O_{(l)}\]

For this galvanic cell,

1. write the half-reaction that occurs at each electrode.
2. indicate which electrode is the cathode and which is the anode.
3. indicate which electrode is the positive electrode and which is the negative electrode.

Given: galvanic cell and redox reaction

Asked for: half-reactions, identity of anode and cathode, and electrode assignment as positive or negative

Strategy:

1. Identify the oxidation half-reaction and the reduction half-reaction. Then identify the anode and cathode from the half-reaction that occurs at each electrode.
2. From the direction of electron flow, assign each electrode as either positive or negative.

Solution:

1. A In the reduction half-reaction, nitrate is reduced to nitric oxide. (The nitric oxide would then react with oxygen in the air to form NO₂, with its characteristic red-brown color.) In the oxidation half-reaction, metallic tin is oxidized. The half-reactions corresponding to the actual reactions that occur in the system are as follows:

reduction: NO₃⁻(aq) + 4H⁺(aq) + 3e⁻ → NO(g) + 2H₂O(l)

oxidation: Sn(s) → Sn²⁺(aq) + 2e⁻

Thus nitrate is reduced to NO, while the tin electrode is oxidized to Sn²⁺.

2. Because the reduction reaction occurs at the Pt electrode, it is the cathode. Conversely, the oxidation reaction occurs at the tin electrode, so it is the anode.
3. B Electrons flow from the tin electrode through the wire to the platinum electrode, where they transfer to nitrate. The electric circuit is completed by the salt bridge, which permits the diffusion of cations toward the cathode and anions toward the anode. Because electrons flow from the tin electrode, it must be electrically negative. In contrast, electrons flow toward the Pt electrode, so that electrode must be electrically positive.

Exercise \(\PageIndex{1}\)

Consider a simple galvanic cell consisting of two beakers connected by a salt bridge. One beaker contains a solution of MnO₄⁻ in dilute sulfuric acid and has a Pt electrode. The other beaker contains a solution of Sn²⁺ in dilute sulfuric acid, also with a Pt electrode. When the two electrodes are connected by a wire, current flows and a spontaneous reaction occurs that is described by the following balanced chemical equation:

\[2MnO^−_{4(aq)} + 5Sn^{2+}_{(aq)} + 16H^+_{(aq)} \rightarrow 2Mn^{2+}_{(aq)} + 5Sn^{4+}_{(aq)} + 8H_2O_{(l)}\]

For this galvanic cell,

1. write the half-reaction that occurs at each electrode.
2. indicate which electrode is the cathode and which is the anode.
3. indicate which electrode is positive and which is negative.

Answer:

1. MnO₄⁻(aq) + 8H⁺(aq) + 5e⁻ → Mn²⁺(aq) + 4H₂O(l); Sn²⁺(aq) → Sn⁴⁺(aq) + 2e⁻
2. The Pt electrode in the permanganate solution is the cathode; the one in the tin solution is the anode.
3. The cathode (electrode in beaker that contains the permanganate solution) is positive, and the anode (electrode in beaker that contains the tin solution) is negative.

Cell Potential

In a galvanic cell, current is produced when electrons flow externally through the circuit from the anode to the cathode because of a difference in potential energy between the two electrodes in the electrochemical cell. In the Zn/Cu system, the valence electrons in zinc have a substantially higher potential energy than the valence electrons in copper because of shielding of the s electrons of zinc by the electrons in filled d orbitals. Hence electrons flow spontaneously from zinc to copper(II) ions, forming zinc(II) ions and metallic copper. Just like water flowing spontaneously downhill, which can be made to do work by forcing a waterwheel, the flow of electrons from a higher potential energy to a lower one can also be harnessed to perform work.

Figure \(\PageIndex{1}\): Potential Energy Difference in the Zn/Cu System. The potential energy of a system consisting of metallic \(Zn\) and aqueous Cu²⁺ ions is greater than the potential energy of a system consisting of metallic Cu and aqueous \(Zn^{2+}\) ions. Much of this potential energy difference is because the valence electrons of metallic Zn are higher in energy than the valence electrons of metallic Cu. Because the Zn(s) + Cu²⁺(aq) system is higher in energy by 1.10 V than the Cu(s) + Zn²⁺(aq) system, energy is released when electrons are transferred from Zn to Cu²⁺ to form Cu and Zn²⁺.

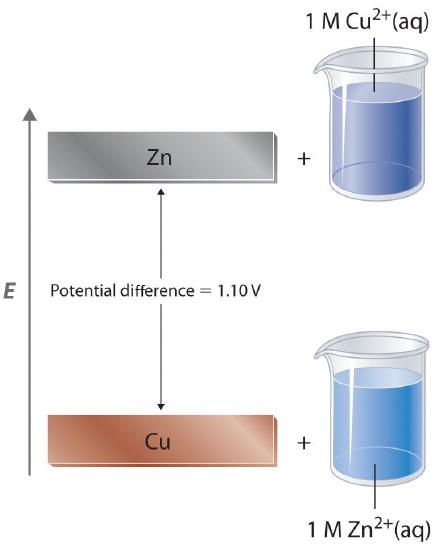
Because the potential energy of valence electrons differs greatly from one substance to another, the voltage of a galvanic cell depends partly on the identity of the reacting substances. If we construct a galvanic cell similar to the one in part (a) in Figure \(\PageIndex{1}\) but instead of copper use a strip of cobalt metal and 1 M Co²⁺ in the cathode compartment, the measured voltage is not 1.10 V but 0.51 V. Thus we can conclude that the difference in potential energy between the valence electrons of cobalt and zinc is less than the difference between the valence electrons of copper and zinc by 0.59 V.

The measured potential of a cell also depends strongly on the concentrations of the reacting species and the temperature of the system. To develop a scale of relative potentials that will allow us to predict the direction of an electrochemical reaction and the magnitude of the driving force for the reaction, the potentials for oxidations and reductions of different substances must be measured under comparable conditions. To do this, chemists use the standard cell potential (E°_cell), defined as the potential of a cell measured under standard conditions—that is, with all species in their standard states (1 M for solutions,Concentrated solutions of salts (about 1 M) generally do not exhibit ideal behavior, and the actual standard state corresponds to an activity of 1 rather than a concentration of 1 M. Corrections for nonideal behavior are important for precise quantitative work but not for the more qualitative approach that we are taking here. 1 atm for gases, pure solids or pure liquids for other substances) and at a fixed temperature, usually 25°C.

Measured redox potentials depend on the potential energy of valence electrons, the concentrations of the species in the reaction, and the temperature of the system.

Measuring Standard Electrode Potentials

It is physically impossible to measure the potential of a single electrode: only the difference between the potentials of two electrodes can be measured (this is analogous to measuring absolute enthalpies or free energies). Recall that only differences in enthalpy and free energy can be measured.) We can, however, compare the standard cell potentials for two different galvanic cells that have one kind of electrode in common. This allows us to measure the potential difference between two dissimilar electrodes. For example, the measured standard cell potential (E°) for the Zn/Cu system is 1.10 V, whereas E° for the corresponding Zn/Co system is 0.51 V. This implies that the potential difference between the Co and Cu electrodes is 1.10 V − 0.51 V = 0.59 V. In fact, that is exactly the potential measured under standard conditions if a cell is constructed with the following cell diagram:

\[Co_{(s)} ∣ Co^{2+}(aq, 1 M)∥Cu^{2+}(aq, 1 M) ∣ Cu (s)\;\;\; E°=0.59\; V \label{20.4.1}\]

This cell diagram corresponds to the oxidation of a cobalt anode and the reduction of Cu²⁺ in solution at the copper cathode.

All tabulated values of standard electrode potentials by convention are listed for a reaction written as a reduction, not as an oxidation, to be able to compare standard potentials for different substances (Table P1). The standard cell potential (E°_cell) is therefore the difference between the tabulated reduction potentials of the two half-reactions, not their sum:

\[E°_{cell} = E°_{cathode} − E°_{anode} \label{20.4.2}\]

In contrast, recall that half-reactions are written to show the reduction and oxidation reactions that actually occur in the cell, so the overall cell reaction is written as the sum of the two half-reactions. According to Equation \(\ref{20.4.2}\), when we know the standard potential for any single half-reaction, we can obtain the value of the standard potential of many other half-reactions by measuring the standard potential of the corresponding cell.

The overall cell reaction is the sum of the two half-reactions, but the cell potential is the difference between the reduction potentials:

\[E°_{cell} = E°_{cathode} − E°_{anode}\]

Figure \(\PageIndex{2}\): The Standard Hydrogen Electrode. The SHE consists of platinum wire that is connected to a Pt surface in contact with an aqueous solution containing 1 M H⁺ in equilibrium with H₂ gas at a pressure of 1 atm. In the molecular view, the Pt surface catalyzes the oxidation of hydrogen molecules to protons or the reduction of protons to hydrogen gas. (Water is omitted for clarity.) The standard potential of the SHE is arbitrarily assigned a value of 0 V.

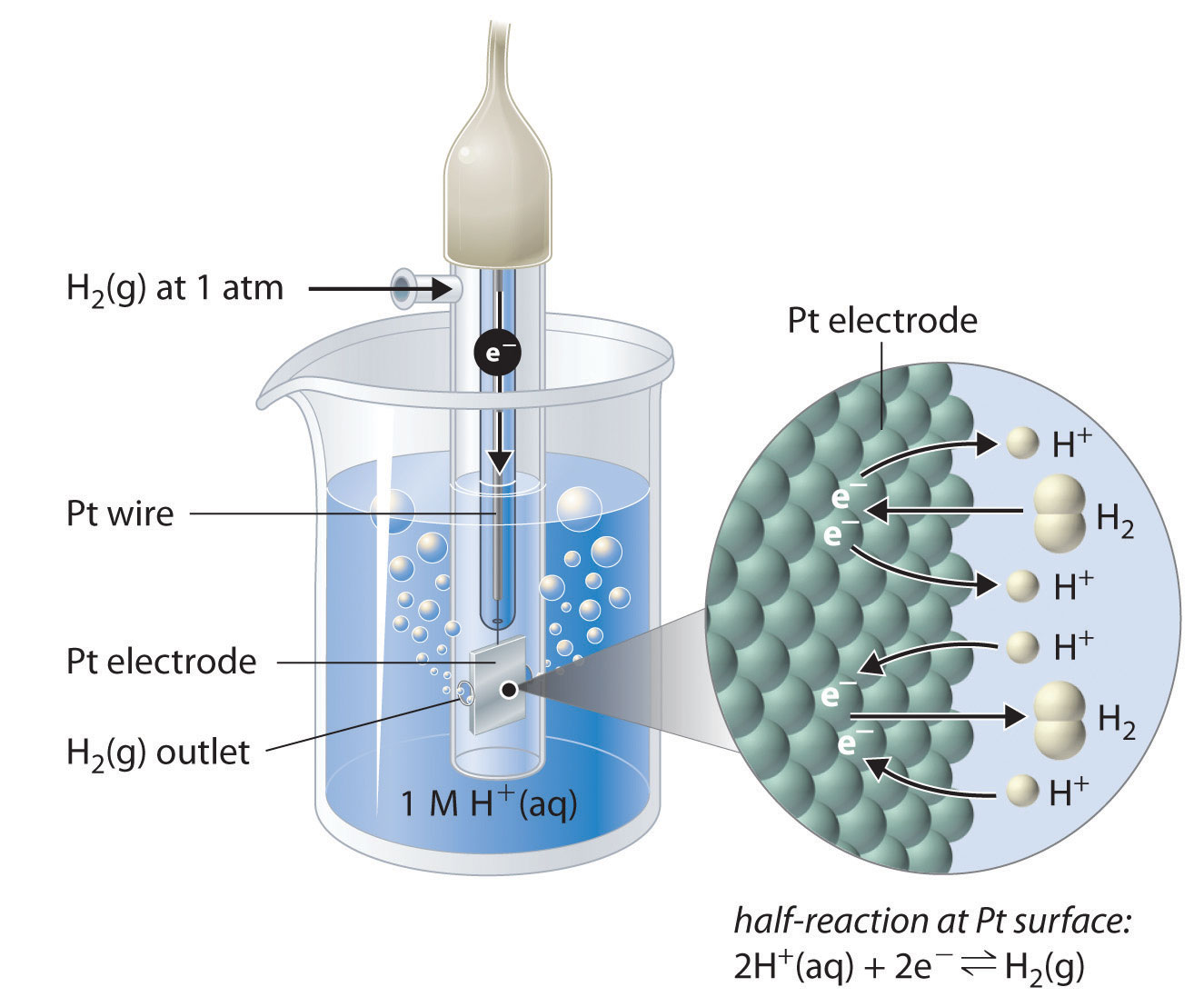
Although it is impossible to measure the potential of any electrode directly, we can choose a reference electrode whose potential is defined as 0 V under standard conditions. The standard hydrogen electrode (SHE) is universally used for this purpose and is assigned a standard potential of 0 V. It consists of a strip of platinum wire in contact with an aqueous solution containing 1 M H⁺. The [H⁺] in solution is in equilibrium with H₂ gas at a pressure of 1 atm at the Pt-solution interface (Figure \(\PageIndex{2}\)). Protons are reduced or hydrogen molecules are oxidized at the Pt surface according to the following equation:

\[2H^+_{(aq)}+2e^− \rightleftharpoons H_{2(g)} \label{20.4.3}\]

One especially attractive feature of the SHE is that the Pt metal electrode is not consumed during the reaction.

Figure \(\PageIndex{3}\): Determining a Standard Electrode Potential Using a Standard Hydrogen Electrode. The voltmeter shows that the standard cell potential of a galvanic cell consisting of a SHE and a Zn/Zn²⁺ couple is \(E°_{cell}\) = 0.76 V. Because the zinc electrode in this cell dissolves spontaneously to form Zn²⁺(aq) ions while H⁺(aq) ions are reduced to H₂ at the platinum surface, the standard electrode potential of the Zn²⁺/Zn couple is −0.76 V.

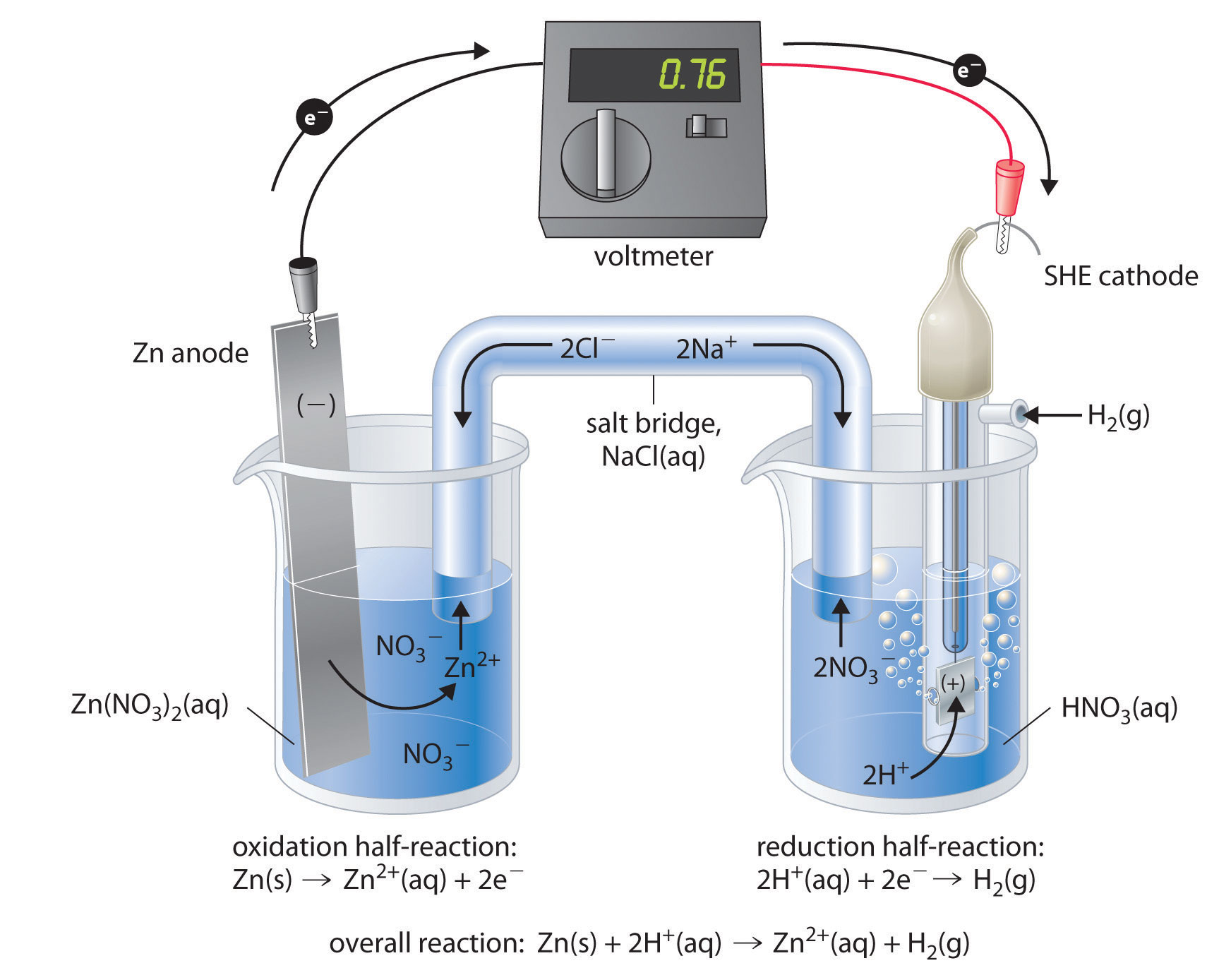
Figure \(\PageIndex{3}\) shows a galvanic cell that consists of a SHE in one beaker and a Zn strip in another beaker containing a solution of Zn²⁺ ions. When the circuit is closed, the voltmeter indicates a potential of 0.76 V. The zinc electrode begins to dissolve to form Zn²⁺, and H⁺ ions are reduced to H₂ in the other compartment. Thus the hydrogen electrode is the cathode, and the zinc electrode is the anode. The diagram for this galvanic cell is as follows:

\[Zn_{(s)}∣Zn^{2+}_{(aq)}∥H^+(aq, 1 M)∣H_2(g, 1 atm)∣Pt_{(s)} \label{20.4.4}\]

The half-reactions that actually occur in the cell and their corresponding electrode potentials are as follows:

• cathode: \[2H^+_{(aq)} + 2e^− \rightarrow H_{2(g)}\;\;\; E°_{cathode}=0 V \label{20.4.5}\]
• anode: \[Zn_{(s)} \rightarrow Zn^{2+}_{(aq)}+2e^−\;\;\; E°_{anode}=−0.76\; V \label{20.4.6}\]

• overall: \[Zn_{(s)}+2H^+_{(aq)} \rightarrow Zn^{2+}_{(aq)}+H_{2(g)} \label{20.4.7}\]

\[E°_{cell}=E°_{cathode}−E°_{anode}=0.76\; V\]

Although the reaction at the anode is an oxidation, by convention its tabulated E° value is reported as a reduction potential. The potential of a half-reaction measured against the SHE under standard conditions is called the standard electrode potential for that half-reaction.In this example, the standard reduction potential for Zn²⁺(aq) + 2e⁻ → Zn(s) is −0.76 V, which means that the standard electrode potential for the reaction that occurs at the anode, the oxidation of Zn to Zn²⁺, often called the Zn/Zn²⁺ redox couple, or the Zn/Zn²⁺ couple, is −(−0.76 V) = 0.76 V. We must therefore subtract E°_anode from E°_cathode to obtain

\[E°_{cell}: 0 \,V − (−0.76\, V) = 0.76\, V\]

Because electrical potential is the energy needed to move a charged particle in an electric field, standard electrode potentials for half-reactions are intensive properties and do not depend on the amount of substance involved. Consequently, E° values are independent of the stoichiometric coefficients for the half-reaction, and, most important, the coefficients used to produce a balanced overall reaction do not affect the value of the cell potential.

E° values do NOT depend on the stoichiometric coefficients for a half-reaction, because it is an intensive property.

Summary

A galvanic (voltaic) cell uses the energy released during a spontaneous redox reaction to generate electricity, whereas an electrolytic cell consumes electrical energy from an external source to force a reaction to occur. Electrochemistry is the study of the relationship between electricity and chemical reactions. The oxidation–reduction reaction that occurs during an electrochemical process consists of two half-reactions, one representing the oxidation process and one the reduction process. The sum of the half-reactions gives the overall chemical reaction. The overall redox reaction is balanced when the number of electrons lost by the reductant equals the number of electrons gained by the oxidant. An electric current is produced from the flow of electrons from the reductant to the oxidant. An electrochemical cell can either generate electricity from a spontaneous redox reaction or consume electricity to drive a nonspontaneous reaction. In a galvanic (voltaic) cell, the energy from a spontaneous reaction generates electricity, whereas in an electrolytic cell, electrical energy is consumed to drive a nonspontaneous redox reaction. Both types of cells use two electrodes that provide an electrical connection between systems that are separated in space. The oxidative half-reaction occurs at the anode, and the reductive half-reaction occurs at the cathode. A salt bridge connects the separated solutions, allowing ions to migrate to either solution to ensure the system’s electrical neutrality. A voltmeter is a device that measures the flow of electric current between two half-reactions. The potential of a cell, measured in volts, is the energy needed to move a charged particle in an electric field. An electrochemical cell can be described using line notation called a cell diagram, in which vertical lines indicate phase boundaries and the location of the salt bridge. Resistance to the flow of charge at a boundary is called the junction potential.