11.8: Temperature and Molecular Velocities

Boltzmann Distributions

At any given time, what fraction of the molecules in a particular sample has a given speed? Some of the molecules will be moving more slowly than average, and some will be moving faster than average, but how many in each situation? . This problem was solved mathematically by Maxwell in 1866; he used statistical analysis to obtain an equation that describes the distribution of molecular speeds at a given temperature. Typical curves showing the distributions of speeds of molecules at several temperatures are displayed in Figure 10.7.1. Increasing the temperature has two effects. First, the peak of the curve moves to the right because the most probable speed increases. Second, the curve becomes broader because of the increased spread of the speeds. Thus increased temperature increases the value of the most probable speed but decreases the relative number of molecules that have that speed. Although the mathematics behind curves such as those in Figure 10.7.1 were first worked out by Maxwell, the curves are almost universally referred to as Boltzmann distributions, after one of the other major figures responsible for the kinetic molecular theory of gases.

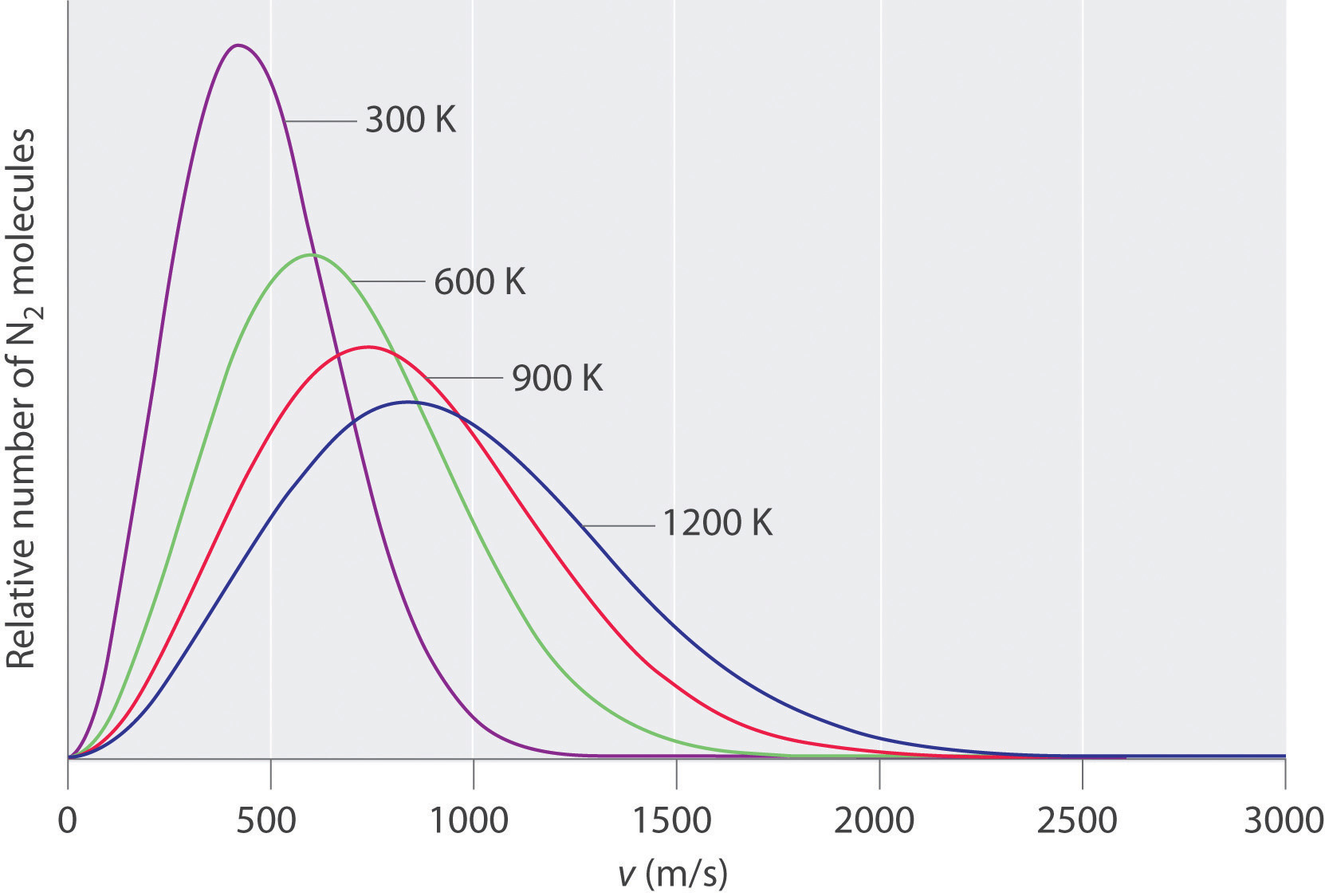
Figure 10.7.2 The Distributions of Molecular Speeds for a Sample of Nitrogen Gas at Various Temperatures. Increasing the temperature increases both the most probable speed (given at the peak of the curve) and the width of the curve.