2.7: Solving Problems Involving Equations
- Page ID
- 25449
Many problems in chemistry involve manipulating equations and require the use of multiple conversion steps. Such problems easy to solve as numerical problems once you understand how to approach them. The four simple steps in problem solving are READ-PLAN-SOLVE-CHECK approach.
- READ the question: Before you start calculating and manipulating equations, read the complete problem thoroughly to ensure you understand what being asked.
- PLAN your approach:
- Write down all of the information you have been given. It is not uncommon that problems will give more facts than are required to solve - this is a bit of reality in the problem.
- Identify the equation(s) that are required to use to solve the problem, this often requires manipulating one or more equations to give you the desired answer.
- SOLVE the problem
- Before calculating results, confirm the correct units required for the equations. You may often are required perform one or more unit conversions before directly using the equations.
- Insert the relevant parameters into the equation(s) and get your answer. Do not forget that most answers will involve units.
- CHECK your answer: Confirm that you have answered all that is requested in the problem and that the answer seems reasonable. For example, if you are calculating the volume of a sample and your calculated results in cubic kilometers, you probably made an error in a conversion or calculation (unless you are working in an astronomy class).
| Example \(\PageIndex{1}\) | Example \(\PageIndex{2}\) | |
|---|---|---|
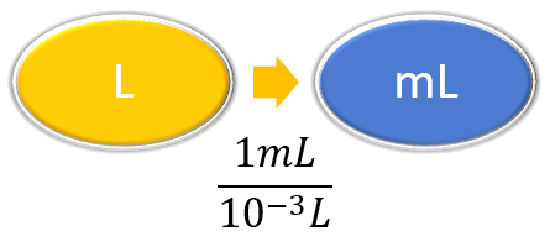
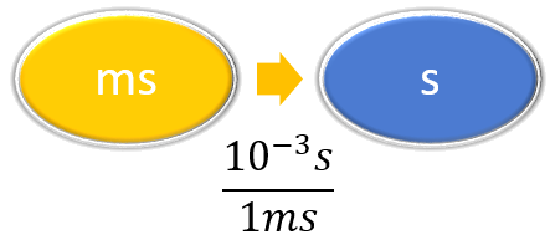
| Steps for Problem Solving | The average volume of blood in an adult male is 4.7 L. What is this volume in milliliters? | A hummingbird can flap its wings once in 18 ms. How many seconds are in 18 ms? |
| Identify the "given"information and what the problem is asking you to "find." | Given: 4.7 L Find: mL |
Given: 18 ms Find: s |
| List other known quantities | \(1\, mL = 10^{-3} L \) | \(1 \,ms = 10^{-3} s \) |
|
Prepare a concept map and use the proper conversion factor. |
 |
 |
| Cancel units and calculate. |
\( 4.7 \cancel{\rm{L}} \times \dfrac{1 \; \rm{mL}}{10^{-3}\; \cancel{\rm{L}}} = 4,700\; \rm{mL}\) \( 4.7 \cancel{\rm{L}} \times \dfrac{1,000 \; \rm{mL}}{1\; \cancel{\rm{L}}} = 4,700\; \rm{mL}\) |
\( 18 \; \cancel{\rm{ms}} \times \dfrac{10^{-3}\; \rm{s}}{1 \; \cancel{\rm{ms}}} = 0.018\; \rm{s}\) or \( 18 \; \cancel{\rm{ms}} \times \dfrac{1\; \rm{s}}{1,000 \; \cancel{\rm{ms}}} = 0.018\; \rm{s}\) |
| Think about your result. | The amount in mL should be 1000 times larger than the given amount in L. | The amount in s should be 1/1000 the given amount in ms. |
Contributions & Attributions
This page was constructed from content via the following contributor(s) and edited (topically or extensively) by the LibreTexts development team to meet platform style, presentation, and quality:
Henry Agnew (UC Davis)

