2.5: Converting between Units
- Page ID
- 25447
- To convert a value reported in one unit to a corresponding value in a different unit using conversion factors.
Earlier we showed how unity factors can be used to express quantities in different units of the same parameter. For example, a density can be expressed in g/cm3 or lb/ft3. Now we will see how conversion factors representing mathematical functions, like \(\rho = m / V\), can be used to transform quantities into different parameters. For example, what is the volume of a given mass of gold? Unity factors and conversion factors are conceptually different, and we'll see that the "dimensional analysis" we develop for unit conversion problems must be used with care in the case of functions.
Conversion Factors
A conversion factor is a factor used to convert one unit of measurement into another. A simple conversion factor can be used to convert meters into centimeters, or a more complex one can be used to convert miles per hour into meters per second. Since most calculations require measurements to be in certain units, you will find many uses for conversion factors. What always must be remembered is that a conversion factor has to represent a fact; this fact can either be simple or much more complex. For instance, you already know that 12 eggs equal 1 dozen. A more complex fact is that the speed of light is \(1.86 \times 10^5\) miles/\(\text{sec}\). Either one of these can be used as a conversion factor depending on what type of calculation you might be working with (Table \(\PageIndex{1}\)).
| English Units | Metric Units | Quantity |
|---|---|---|
| 1 ounce (oz) | 28.35 grams (g) | *mass |
| 1 fluid once (oz) | 29.6 mL | volume |
| 2.205 pounds (lb) | 1 kilogram (kg) | *mass |
| 1 inch (in) | 2.54 centimeters (cm) | length |
| 0.6214 miles (mi) | 1 kilometer (km) | length |
| 1 quarter (qt) | 0.95 liters (L) | volume |
*pounds and ounces are technically units of force, not mass.
Of course, there are other ratios which are not listed in Table \(\PageIndex{1}\). They may include:
- Ratios embedded in the text of the problem (using words such as per or in each, or using symbols such as / or %).
- Conversions in the metric system, as covered earlier in this chapter.
- Common knowledge ratios (such as 60 seconds \(=\) 1 minute).
If you learned the SI units and prefixes described, then you know that 1 cm is 1/100th of a meter.
\[ 1\; \rm{cm} = \dfrac{1}{100} \; \rm{m} = 10^{-2}\rm{m} \nonumber\]
or
\[100\; \rm{cm} = 1\; \rm{m} \nonumber\]
Suppose we divide both sides of the equation by \(1 \text{m}\) (both the number and the unit):
\[\mathrm{\dfrac{100\:cm}{1\:m}=\dfrac{1\:m}{1\:m}} \nonumber\]
As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:
\[ \dfrac{ \text{100 cm}}{\text{1 m}} = \dfrac{ \text{1000 mm}}{\text{1 m}}= \dfrac{ 1\times 10^6 \mu \text{m}}{\text{1 m}}= 1 \nonumber\]
We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units.
Dimensional Analysis
Dimensional analysis is amongst the most valuable tools physical scientists use. Simply put, it is the conversion between an amount in one unit to the corresponding amount in a desired unit using various conversion factors. This is valuable because certain measurements are more accurate or easier to find than others. The use of units in a calculation to ensure that we obtain the final proper units is called dimensional analysis.
Here is a simple example. How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a conversion factor, which is the same as multiplying it by 1. We can write 1 as \(\mathrm{\frac{100\:cm}{1\:m}}\) and multiply:
\[ 3.55 \; \rm{m} \times \dfrac{100 \; \rm{cm}}{1\; \rm{m}} \nonumber\]
The 3.55 m can be thought of as a fraction with a 1 in the denominator. Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out:
\[\dfrac{3.55 \; \cancel{\rm{m}}}{ 1} \times \dfrac{100 \; \rm{cm}}{1 \; \cancel{\rm{m}}} \nonumber\]
The final step is to perform the calculation that remains once the units have been canceled:
\[ \dfrac{3.55}{1} \times \dfrac{100 \; \rm{cm}}{1} = 355 \; \rm{cm} \nonumber\]
In the final answer, we omit the 1 in the denominator. Thus, by a more formal procedure, we find that 3.55 m equals 355 cm. A generalized description of this process is as follows:
\[\text{quantity}\, \cancel{(\text{old units})} \times \underbrace{\left( \dfrac{\text{new units}}{\cancel{\text{old units}}}\right) }_{\text{conversion factor}=1} = \text{quantity (new units)}\]
You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. In later studies, the conversion problems you will encounter will not always be so simple. If you can master the technique of applying conversion factors, you will be able to solve a large variety of problems.
In the previous example, we used the fraction \(\frac{100 \; \rm{cm}}{1 \; \rm{m}}\) as a conversion factor. Does the conversion factor \(\frac{1 \; \rm m}{100 \; \rm{cm}}\) also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are expressed in different units). Why did we not use that conversion factor? If we had used the second conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:
\[ 3.55 \; \rm{m} \times \dfrac{1\; \rm{m}}{100 \; \rm{cm}} = 0.0355 \dfrac{\rm{m}^2}{\rm{cm}} \nonumber\]
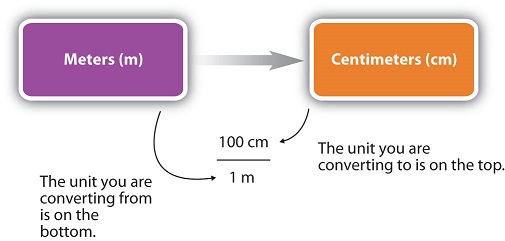
For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out. Figure \(\PageIndex{1}\) shows a concept map for constructing a proper conversion.
Perform each conversion.
- 101,000. ns to seconds
- 32.08 kg to grams
- 1.53 grams to cg
- Answer a
- \(1.01000 \times 10^{-4} s \)
- Answer b
- \(3.208 \times 10^{4} g \)
- Answer c
- \(1.53 \times 10^{2} g \)
Summary
- Conversion factors are used to convert one unit of measurement into another.
- Dimensional analysis (unit conversions) involves the use of conversion factors that will cancel units you don't want and produce units you do want.
Contributions & Attributions
This page was constructed from content via the following contributor(s) and edited (topically or extensively) by the LibreTexts development team to meet platform style, presentation, and quality:
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.
Henry Agnew (UC Davis)