1.9: Atomic Mass- The Average Mass of an Element’s Atoms
- Page ID
- 274045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- to know the meaning of isotopes and atomic masses.
There are 21 elements with only one isotope, so all their atoms have identical masses. All other elements have two or more isotopes, so their atoms have at least two different masses. However, all elements obey the law of definite proportions when they combine with other elements, so they behave as if they had just one kind of atom with a definite mass. To solve this dilemma, we define the atomic mass as the weighted average mass of all naturally occurring isotopes of the element.
A atomic mass is defined as
\[\text{Atomic mass} = \left(\dfrac{\%\text{ abundance isotope 1}}{100}\right)\times \left(\text{mass of isotope 1}\right) + \left(\dfrac{\%\text{ abundance isotope 2}}{100}\right)\times \left(\text{mass of isotope 2}\right)~ ~ ~ + ~ ~ ... \label{amass}\]
Similar terms would be added for all the isotopes that would be found in a bulk sample from nature.
The weighted average is analogous to the method used to calculate grade point averages in most colleges:
\[\text{GPA} = \left(\dfrac{\text{Credit Hours Course 1}}{\text{total credit hours}}\right)\times \left(\text{Grade in Course 1}\right) + \left(\dfrac{\text{Credit Hours Course 2}}{\text{total credit hours}}\right)\times \left(\text{Grade in Course 2}\right)~ + ~... \nonumber\]
The periodic table lists the atomic masses of all the elements. Comparing these values with those given for some of the isotopes reveals that the atomic masses given in the periodic table never correspond exactly to those of any of the isotopes Figure \(\PageIndex{1}\). Because most elements exist as mixtures of several stable isotopes, the atomic mass of an element is defined as the weighted average of the masses of the isotopes. For example, naturally occurring carbon is largely a mixture of two isotopes: 98.89% 12C (mass = 12 amu by definition) and 1.11% 13C (mass = 13.003355 amu). The percent abundance of 14C is so low that it can be ignored in this calculation. The average atomic mass of carbon is then calculated as follows:
\[ \rm(0.9889 \times 12 \;amu) + (0.0111 \times 13.003355 \;amu) = 12.01 \;amu \label{Eq5} \]
Carbon is predominantly 12C, so its average atomic mass should be close to 12 amu, which is in agreement with this calculation.
The value of 12.01 is shown under the symbol for C in the periodic table, although without the abbreviation amu, which is customarily omitted. Thus the tabulated atomic mass of carbon or any other element is the weighted average of the masses of the naturally occurring isotopes.

Naturally occurring lead is found to consist of four isotopes:
- 1.40% \({}_{\text{82}}^{\text{204}}\text{Pb}\) whose isotopic mass is 203.973.
- 24.10% \({}_{\text{82}}^{\text{206}}\text{Pb}\) whose isotopic mass is 205.974.
- 22.10% \({}_{\text{82}}^{\text{207}}\text{Pb}\) whose isotopic mass is 206.976.
- 52.40% \({}_{\text{82}}^{\text{208}}\text{Pb}\) whose isotopic mass is 207.977.
Calculate the atomic mass of an average naturally occurring sample of lead.
Solution
This is a direct application of Equation \ref{amass} and is best calculated term by term.
Suppose that you had 1 mol lead. This would contain 1.40% (\(\dfrac{1.40}{100}\) × 1 mol) \({}_{\text{82}}^{\text{204}}\text{Pb}\) whose molar mass is 203.973 g mol–1. The mass of 20482Pb would be
\[\begin{align*} \text{m}_{\text{204}} &=n_{\text{204}}\times \text{ }M_{\text{204}} \\[4pt] &=\left( \frac{\text{1}\text{.40}}{\text{100}}\times \text{ 1 mol} \right)\text{ (203}\text{.973 g mol}^{\text{-1}}\text{)} \\[4pt] &=\text{2}\text{0.86 g} \end{align*}\]
Similarly for the other isotopes
\[\begin{align*}\text{m}_{\text{206}}&=n_{\text{206}}\times \text{ }M_{\text{206}}\\[4pt] &=\left( \frac{\text{24}\text{.10}}{\text{100}}\times \text{ 1 mol} \right)\text{ (205}\text{.974 g mol}^{\text{-1}}\text{)}\\[4pt] &=\text{49}\text{0.64 g} \\[6pt]\text{m}_{\text{207}}&=n_{\text{207}}\times \text{ }M_{\text{207}}\\[4pt] &=\left( \frac{\text{22}\text{.10}}{\text{100}}\times \text{ 1 mol} \right)\text{ (206}\text{.976 g mol}^{\text{-1}}\text{)}\\[4pt] &=\text{45}\text{0.74 g} \\[6pt] \text{m}_{\text{208}}&=n_{\text{208}}\times \text{ }M_{\text{208}}\\[4pt] &=\left( \frac{\text{52}\text{.40}}{\text{100}}\times \text{ 1 mol} \right)\text{ (207}\text{.977 g mol}^{\text{-1}}\text{)}\\[4pt] &=\text{108}\text{0.98 g} \end{align*}\]
Upon summing all four results, the mass of 1 mol of the mixture of isotopes is to be found
\[2.86\, g + 49.64\, g + 45.74\, g + 108.98\, g = 207.22\, g\nonumber\]
The mass of an average lead atom, and thus lead's atomic mass, is 207.2 g/mol. This should be confirmed by consulting the Periodic Table of the Elements.
Boron has two naturally occurring isotopes. In a sample of boron, \(20\%\) of the atoms are \(\ce{B}-10\), which is an isotope of boron with 5 neutrons and mass of \(10 \: \text{amu}\). The other \(80\%\) of the atoms are \(\ce{B}-11\), which is an isotope of boron with 6 neutrons and a mass of \(11 \: \text{amu}\). What is the atomic mass of boron?
- Answer
-
The mass of an average boron atom, and thus boron's atomic mass, is \(10.8 \: \text{amu}\). This should be confirmed by consulting the Periodic Table of the Elements.
An important corollary to the existence of isotopes should be emphasized at this point. When highly accurate results are obtained, atomic weights may vary slightly depending on where a sample of an element was obtained. For this reason, the Commission on Isotopic Abundance and Atomic Weights of IUPAC (IUPAC/CIAAWhas redefined the atomic masses of 10 elements having two or more isotopes. The percentages of different isotopes often depends on the source of the element.
For example, oxygen in Antarctic precipitation has an atomic weight of 15.99903, but oxygen in marine \(\ce{N2O}\) has an atomic mass of 15.9997. "Fractionation" of the isotopes results from slightly different rates of chemical and physical processes caused by small differences in their masses. The difference can be more dramatic when an isotope is derived from nuclear reactors.
Mass Spectrometry: Measuring the Mass of Atoms and Molecules
Although the masses of the electron, the proton, and the neutron are known to a high degree of precision, the mass of any given atom is not simply the sum of the masses of its electrons, protons, and neutrons. For example, the ratio of the masses of 1H (hydrogen) and 2H (deuterium) is actually 0.500384, rather than 0.49979 as predicted from the numbers of neutrons and protons present. Although the difference in mass is small, it is extremely important because it is the source of the huge amounts of energy released in nuclear reactions.
Because atoms are much too small to measure individually and do not have charges, there is no convenient way to accurately measure absolute atomic masses. Scientists can measure relative atomic masses very accurately, however, using an instrument called a mass spectrometer. The technique is conceptually similar to the one Thomson used to determine the mass-to-charge ratio of the electron. First, electrons are removed from or added to atoms or molecules, thus producing charged particles called ions. When an electric field is applied, the ions are accelerated into a separate chamber where they are deflected from their initial trajectory by a magnetic field, like the electrons in Thomson’s experiment. The extent of the deflection depends on the mass-to-charge ratio of the ion. By measuring the relative deflection of ions that have the same charge, scientists can determine their relative masses (Figure \(\PageIndex{2}\)). Thus it is not possible to calculate absolute atomic masses accurately by simply adding together the masses of the electrons, the protons, and the neutrons, and absolute atomic masses cannot be measured, but relative masses can be measured very accurately. It is actually rather common in chemistry to encounter a quantity whose magnitude can be measured only relative to some other quantity, rather than absolutely. We will encounter many other examples later in this text. In such cases, chemists usually define a standard by arbitrarily assigning a numerical value to one of the quantities, which allows them to calculate numerical values for the rest.
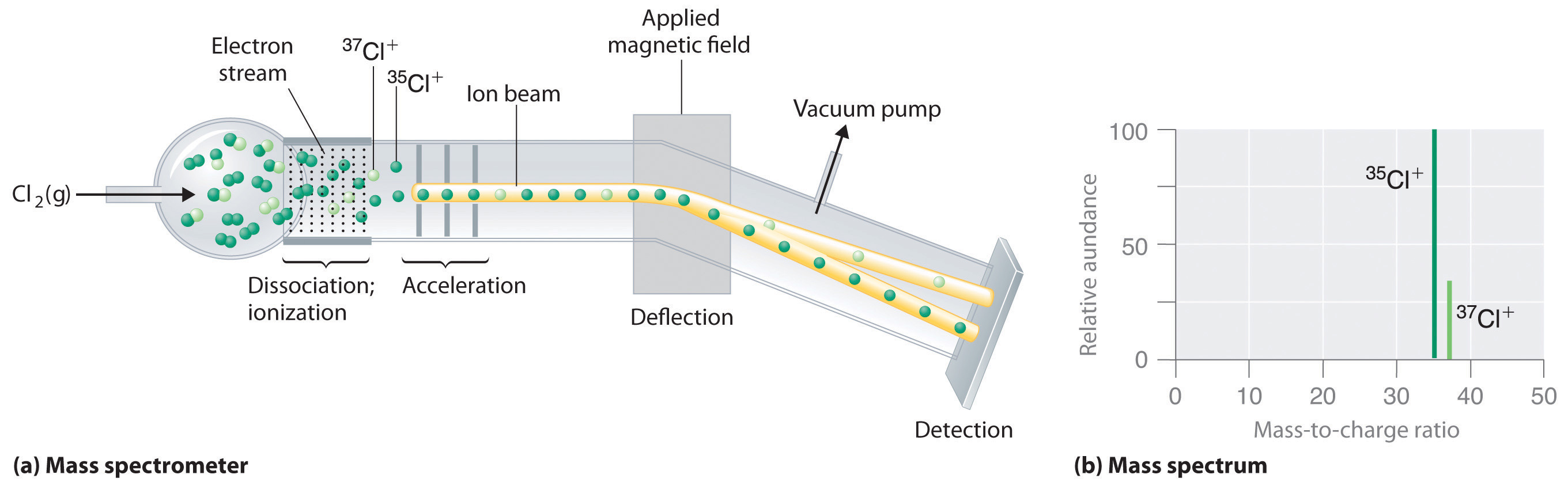
The arbitrary standard that has been established for describing atomic mass is the atomic mass unit (amu or u), defined as one-twelfth of the mass of one atom of 12C. Because the masses of all other atoms are calculated relative to the 12C standard, 12C is the only atom whose exact atomic mass is equal to the mass number. Experiments have shown that 1 amu = 1.66 × 10−24 g.
Mass spectrometric experiments give a value of 0.167842 for the ratio of the mass of 2H to the mass of 12C, so the absolute mass of 2H is
\[\rm{\text{mass of }^2H \over \text{mass of }^{12}C} \times \text{mass of }^{12}C = 0.167842 \times 12 \;amu = 2.104104\; amu \label{Eq4}\]
The masses of the other elements are determined in a similar way.
Naturally occurring bromine consists of the two isotopes listed in the following table:
| Isotope | Exact Mass (amu) | Percent Abundance (%) |
|---|---|---|
| 79Br | 78.9183 | 50.69 |
| 81Br | 80.9163 | 49.31 |
Calculate the atomic mass of bromine.
Given: exact mass and percent abundance
Asked for: atomic mass
Strategy:
- Convert the percent abundances to decimal form to obtain the mass fraction of each isotope.
- Multiply the exact mass of each isotope by its corresponding mass fraction (percent abundance ÷ 100) to obtain its weighted mass.
- Add together the weighted masses to obtain the atomic mass of the element.
- Check to make sure that your answer makes sense.
Solution:
A The atomic mass is the weighted average of the masses of the isotopes (Equation \ref{amass}. In general, we can write
Bromine has only two isotopes. Converting the percent abundances to mass fractions gives
\[\ce{^{79}Br}: {50.69 \over 100} = 0.5069 \nonumber\]
B Multiplying the exact mass of each isotope by the corresponding mass fraction gives the isotope’s weighted mass:
\(\ce{^{79}Br}: 79.9183 \;amu \times 0.5069 = 40.00\; amu\)
\(\ce{^{81}Br}: 80.9163 \;amu \times 0.4931 = 39.90 \;amu\)
C The sum of the weighted masses is the atomic mass of bromine is
40.00 amu + 39.90 amu = 79.90 amu
D This value is about halfway between the masses of the two isotopes, which is expected because the percent abundance of each is approximately 50%.
Magnesium has the three isotopes listed in the following table:
| Isotope | Exact Mass (amu) | Percent Abundance (%) |
|---|---|---|
| 24Mg | 23.98504 | 78.70 |
| 25Mg | 24.98584 | 10.13 |
| 26Mg | 25.98259 | 11.17 |
Use these data to calculate the atomic mass of magnesium.
- Answer
-
24.31 amu
Summary
The mass of an atom is a weighted average that is largely determined by the number of its protons and neutrons, whereas the number of protons and electrons determines its charge. Each atom of an element contains the same number of protons, known as the atomic number (Z). Neutral atoms have the same number of electrons and protons. Atoms of an element that contain different numbers of neutrons are called isotopes. Each isotope of a given element has the same atomic number but a different mass number (A), which is the sum of the numbers of protons and neutrons. The relative masses of atoms are reported using the atomic mass unit (amu), which is defined as one-twelfth of the mass of one atom of carbon-12, with 6 protons, 6 neutrons, and 6 electrons. The atomic mass of an element is the weighted average of the masses of the naturally occurring isotopes. When one or more electrons are added to or removed from an atom or molecule, a charged particle called an ion is produced, whose charge is indicated by a superscript after the symbol.
Contributors and Attributions
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.

