1.6: The Discovery of the Electron
- Page ID
- 25459
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To become familiar with the feature of an electron.
- Summarize and interpret the results of the experiments of Thomson and Millikan.
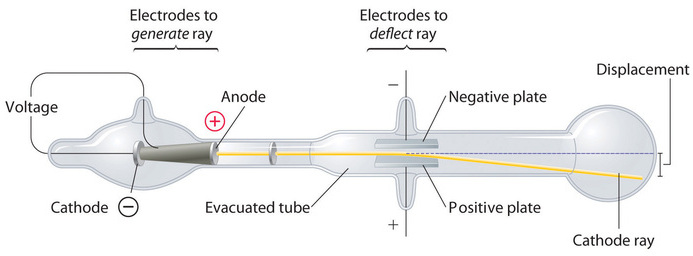
Long before the end of the 19th century, it was well known that applying a high voltage to a gas contained at low pressure in a sealed tube (called a gas discharge tube) caused electricity to flow through the gas, which then emitted light (Figure \(\PageIndex{1}\)). Researchers trying to understand this phenomenon found that an unusual form of energy was also emitted from the cathode, or negatively charged electrode; this form of energy was called a "cathode ray". In 1897, the British physicist J. J. Thomson (1856–1940) proved that atoms were not the most basic form of matter. He demonstrated that cathode rays could be deflected, or bent, by magnetic or electric fields, which indicated that cathode rays consist of charged particles.
More important, by measuring the extent of the deflection of the cathode rays in magnetic or electric fields of various strengths, Thomson was able to calculate the mass-to-charge ratio of the particles. These particles were emitted by the negatively charged cathode and repelled by the negative terminal of an electric field. Because like charges repel each other and opposite charges attract, Thomson concluded that the particles had a net negative charge; these particles are now called electrons. Most relevant to the field of chemistry, Thomson found that the mass-to-charge ratio of cathode rays is independent of the nature of the metal electrodes or the gas, which suggested that electrons were fundamental components of all atoms.
If two objects each have electric charge, then they exert an exert an electric force on each other. The magnitude of the force is linearly proportional the charge on each object and inversely proportional to square distance between each other. The magnitude of this electrostatic force is linearly proportional the distance between them and involves the existence of two types of charge, the observation that like charges repel, unlike charges attract and the decrease of force with distance.

The SI unit of electric charge is the coulomb (C) named after French physicist Charles-Augustin de Coulomb.
The video below shows JJ Thompson used such tube to measure the ratio of charge over mass of an electron.
Millikan’s Oil Drop Experiment: Measuring the Charge of the Electron
The American scientist Robert Millikan (1868–1953) carried out a series of experiments using electrically charged oil droplets, which allowed him to calculate the charge on a single electron. Millikan created microscopic oil droplets, which could be electrically charged by friction as they formed or by using X-rays. These droplets initially fell due to gravity, but their downward progress could be slowed or even reversed by an electric field lower in the apparatus. By adjusting the electric field strength and making careful measurements and appropriate calculations, Millikan was able to determine the charge on individual drops (Figure \(\PageIndex{2}\)).
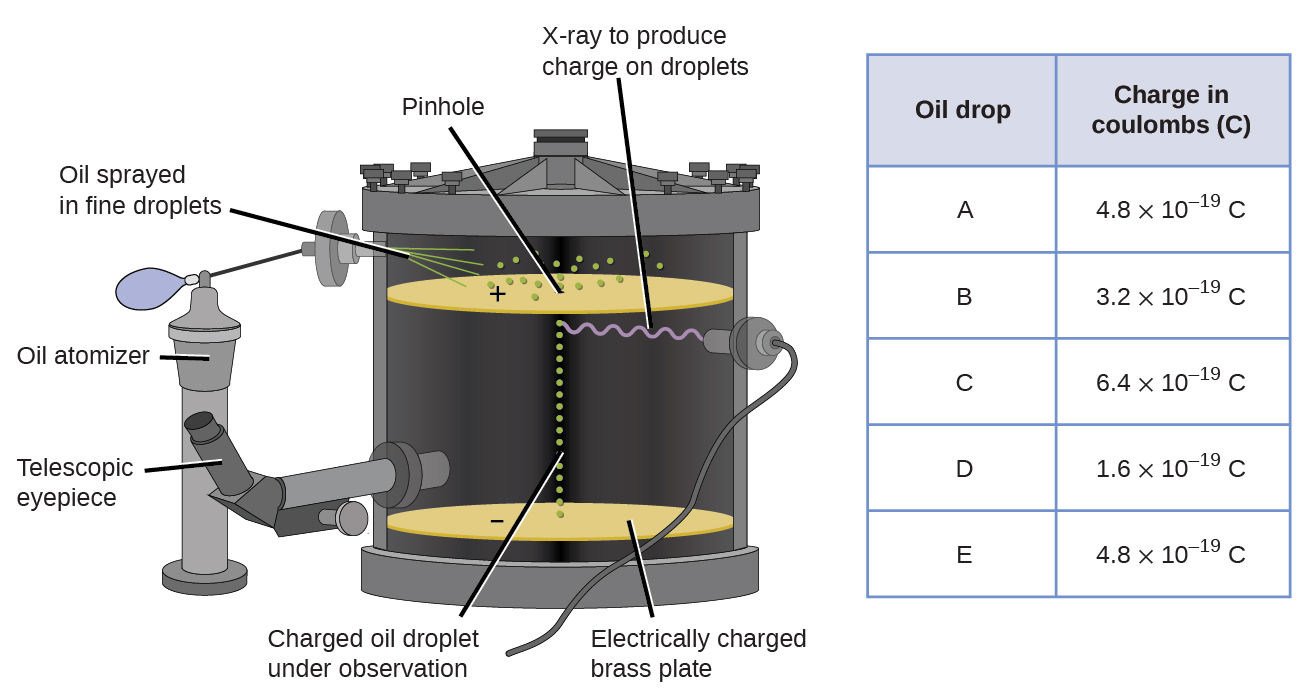
Looking at the charge data that Millikan gathered, you may have recognized that the charge of an oil droplet is always a multiple of a specific charge, \(1.6 \times 10^{−19}\, C\). Millikan concluded that this value must therefore be a fundamental charge—the charge of a single electron—with his measured charges due to an excess of one electron (\(1 \times (1.6 \times 10^{−19}\, C)\)), two electrons (\(2 \times (1.6 \times 10^{−19}\, C)\)), three electrons (\(3 \times (1.6 \times 10^{−19}\, C)\)), and so on, on a given oil droplet.
The charge of an electron is sometimes referred to as the elementary charge and usually denoted by \(e\). The elementary charge is a fundamental physical constant and as of May 2019, its value is defined to be exactly \(1.602176634 \times 10^{−19}\, C\).
Since the charge of an electron was now known due to Millikan’s research, and the charge-to-mass ratio was already known due to Thomson’s research (\(1.759 \times 10^{11}\, C/kg\)), it only required a simple calculation to determine the mass of the electron as well.
\[\begin{align*} \mathrm{Mass\: of\: electron} &= \mathrm{1.602\times 10^{-19}\:\cancel{C}\times \dfrac{1\: kg}{1.759\times 10^{11}\:\cancel{C}}} \\[4pt] &= \mathrm{9.107\times 10^{-31}\:kg} \end{align*}\]
Scientists had now established that the atom was not indivisible as Dalton's theory had postulated, and due to the work of Thomson, Millikan, and others, the charge and mass of the negative, subatomic particles—the electrons—were known. However, the positively charged part of an atom was not yet well understood.
In a Millikan's oil drop experiment done in alternate universe, the measured charges on drops are found to be \(8 \times 10^{-19}\, C\), \(12 \times 10^{-19}\, C \) and \(20 \times 10^{-19}\, C\). What is the elementary charge in this universe?
- Answer
-
Millikan experiment involves confirm that the charges of the drops were all small integer multiples of the elementary charge. The charges on the drop are found to be multiple of 4. Hence the small charge are \(4 \times 10^{-19} C\).
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

