15.1: Classifications of Acids and Bases

Learning Objectives

• To understand the differences between the three definitions of Acids and Bases
• Identify acids, bases, and conjugate acid-base pairs according to the three definitions of Acids and Bases
• To understand the concept of conjugate acid–base pairs in acid/base reactions
• Write the equation for the proton transfer reaction involving a Brønsted-Lowry acid or base, and show how it can be interpreted as an electron-pair transfer reaction, clearly identifying the donor and acceptor.
• Give an example of a Lewis acid-base reaction that does not involve protons.

Acids and bases have been known for a long time. When Robert Boyle characterized them in 1680, he noted that acids dissolve many substances, change the color of certain natural dyes (for example, they change litmus from blue to red), and lose these characteristic properties after coming into contact with alkalis (bases). In the eighteenth century, it was recognized that acids have a sour taste, react with limestone to liberate a gaseous substance (now known to be CO₂), and interact with alkalis to form neutral substances. In 1815, Humphry Davy contributed greatly to the development of the modern acid-base concept by demonstrating that hydrogen is the essential constituent of acids. Around that same time, Joseph Louis Gay-Lussac concluded that acids are substances that can neutralize bases and that these two classes of substances can be defined only in terms of each other. The significance of hydrogen was reemphasized in 1884 when Carl Axel Arrhenius defined an acid as a compound that dissolves in water to yield hydrogen cations (now recognized to be hydronium ions) and a base as a compound that dissolves in water to yield hydroxide anions.

Acids and bases are common solutions that exist everywhere. Almost every liquid that we encounter in our daily lives consists of acidic and basic properties, with the exception of water. They have completely different properties and are able to neutralize to form H₂O, which will be discussed later in a subsection. Acids and bases can be defined by their physical and chemical observations (Table \(\PageIndex{1}\)).

Table \(\PageIndex{1}\): General Properties of Acids and Bases

ACIDS	BASES
produce a piercing pain in a wound.	give a slippery feel.
taste sour.	taste bitter.
are colorless when placed in phenolphthalein (an indicator).	are pink when placed in phenolphthalein (an indicator).
are red on blue litmus paper (a pH indicator).	are blue on red litmus paper (a pH indicator).
have a pH<7.	have a pH>7.
produce hydrogen gas when reacted with metals.
produce carbon dioxide when reacted with carbonates.
Common examples: Lemons, oranges, vinegar, urine, sulfuric acid, hydrochloric acid	Common Examples: Soap, toothpaste, bleach, cleaning agents, limewater, ammonia water, sodium hydroxide.

Acids and bases in aqueous solutions will conduct electricity because they contain dissolved ions. Therefore, acids and bases are electrolytes. Strong acids and bases will be strong electrolytes. Weak acids and bases will be weak electrolytes. This affects the amount of conductivity.

In chemistry, acids and bases have been defined differently by three sets of theories: One is the Arrhenius definition defined above, which revolves around the idea that acids are substances that ionize (break off) in an aqueous solution to produce hydrogen (H⁺) ions while bases produce hydroxide (OH^-) ions in solution. The other two definitions are discussed in detail include the Brønsted-Lowry definition the defines acids as substances that donate protons (H⁺) whereas bases are substances that accept protons and the Lewis theory of acids and bases states that acids are electron pair acceptors while bases are electron pair donors.

Arrhenius Acids and Bases

In 1884, the Swedish chemist Svante Arrhenius proposed two specific classifications of compounds, termed acids and bases. When dissolved in an aqueous solution, certain ions were released into the solution. The Arrhenius definition of acid-base reactions is a development of the "hydrogen theory of acids". It was used to provide a modern definition of acids and bases, and followed from Arrhenius's work with Friedrich Wilhelm Ostwald in establishing the presence of ions in aqueous solution in 1884. This led to Arrhenius receiving the Nobel Prize in Chemistry in 1903.

An Arrhenius acid is a compound that increases the concentration of \(\ce{H^{+}}\) ions that are present when added to water.

\[ \ce{HCl(g) \rightarrow H^{+}(aq) + Cl^{-}(aq)} \label{eq1}\]

In this reaction, hydrochloric acid (\(\ce{HCl}\)) gas dissociates into hydrogen (\(\ce{H^{+}}\)) and chloride (\(\ce{Cl^{-}}\)) ions when dissolved in water, thereby releasing \(\ce{H^{+}}\) ions into solution. These \(\ce{H^{+}}\) ions form the hydronium ion (\(\ce{H_3O^{+}}\)) when they combine with water molecules. Both processes can be represented in a chemical equation by adding \(\ce{H2O}\) to the reactants side of Equation \ref{eq1} and switching hydronium ions for free protons.

\[ \ce{ HCl(g) + H2O(l) \rightarrow H_3O^{+}(aq) + Cl^{-}(aq)} \label{eq2} \]

An Arrhenius base is a compound that dissociates to yield hydroxide ions (\(\ce{OH^{−}}\)) in aqueous solution. Common examples of Arrhenus bases include Sodium hydroxide (\(\ce{NaOH}\)), Potassium hydroxide (\(\ce{KOH}\)), Magnesium hydroxide \(\ce{Mg(OH)2}\), and  Calcium hydroxide (\(\ce{Ca(OH)2}\). All of these bases are solids at room temperature and when dissolved in water, will generate a metal cation and the hydroxide ion (\(\ce(OH^{-}}\)), for example, Sodium hydroxide

\[\ce{NaOH(s) -> Na^{+}(aq) + OH^{-}(aq)} \label{eq3}\]

All Arrhenius acids have easily detachable hydrogen that leave to form hydronium ions in solution and all Arrhenius bases have easily detachable OH groups that form hydroxide ions in solution.

Limitation of the Arrhenius Definition of Acids and Bases

The Arrhenius definitions of acidity and alkalinity are restricted to aqueous solutions and refer to the concentration of the solvated ions. Under this definition, pure \(\ce{H2SO4}\) or \(\ce{HCl}\) dissolved in toluene are not acidic, despite the fact that both of these acids will donate a proton to toluene. In addition, under the Arrhenius definition, a solution of sodium amide (\(\ce{NaNH2}\)) in liquid ammonia is not alkaline, despite the fact that the amide ion (\(\ce{NH2^{-}}\)) will readily deprotonate ammonia. Thus, the Arrhenius definition can only describe acids and bases in an aqueous environment. The Arrhenius definition can only describe acids and bases in protic solvents and environments (e.g., water, alcohols, within proteins etc.).

Brønsted-Lowry Acids and Bases

The Arrhenius definitions identified an acid as a compound that dissolves in water to yield hydronium ions (Equation \ref{eq2}\) and a base as a compound that dissolves in water to yield hydroxide ions (Equation \ref{eq3}). As mentioned above, this definition limited. We extended the definition of an acid or a base using the more general definition proposed in 1923 by the Danish chemist Johannes Brønsted and the English chemist Thomas Lowry. Their definition centers on the proton, \(\ce{H^+}\). A proton is what remains when a normal hydrogen atom, \(\ce{^1_1H}\), loses an electron. A compound that donates a proton to another compound is called a Brønsted-Lowry acid, and a compound that accepts a proton is called a Brønsted-Lowry base. An acid-base reaction is the transfer of a proton from a proton donor (acid) to a proton acceptor (base).

Acids may be compounds such as \(\ce{HCl}\) or \(\ce{H2SO4}\), organic acids like acetic acid (\(\ce{CH_3COOH}\)) or ascorbic acid (vitamin C), or \(\ce{H2O}\). Anions (such as \(\ce{HSO_4^-}\), \(\ce{H_2PO_4^-}\), \(\ce{HS^-}\), and \(\ce{HCO_3^-}\)) and cations (such as \(\ce{H_3O^+}\), \(\ce{NH_4^+}\), and \(\ce{[Al(H_2O)_6]^{3+}}\)) may also act as acids.

Bases fall into the same three categories and may be neutral molecules (such as \(\ce{H_2O}\), \(\ce{NH_3}\), and \(\ce{CH_3NH_2}\)), anions (such as \(\ce{OH^-}\), \(\ce{HS^-}\), \(\ce{HCO_3^-}\), \(\ce{CO_3^{2−}}\), \(\ce{F^-}\), and \(\ce{PO_4^{3−}}\)), or cations (such as \(\ce{[Al(H_2O)_5OH]^{2+}}\)). The most familiar bases are ionic compounds such as \(\ce{NaOH}\) and \(\ce{Ca(OH)_2}\), which contain the hydroxide ion, \(\ce{OH^-}\). The hydroxide ion in these compounds accepts a proton from acids to form water:

\[\ce{H^+ + OH^- \rightarrow H_2O} \label{15.1.1}\]

We call the product that remains after an acid donates a proton the conjugate base of the acid. This species is a base because it can accept a proton (to re-form the acid):

\[\begin{align*} \text{acid} &\rightleftharpoons \text{proton} + \text{conjugate base} \\[4pt] \ce{HF} &\rightleftharpoons \ce{H^+ + F^-} \\[4pt]  \ce{H_2SO_4} &\rightleftharpoons \ce{H^+ + HSO_4^{−}} \\[4pt] \ce{H_2O} &\rightleftharpoons \ce{H^+ + OH^-} \\[4pt] \ce{HSO_4^-} &\rightleftharpoons \ce{H^+ + SO_4^{2−}} \\[4pt] \ce{NH_4^+} &\rightleftharpoons \ce{H^+ + NH_3} \end{align*}\]

We call the product that results when a base accepts a proton the base’s conjugate acid. This species is an acid because it can give up a proton (and thus re-form the base):

\[\begin{align*} \text{base} + \text{proton} &\rightleftharpoons \text{conjugate acid} \\[4pt] \ce{OH^- + H^+} &\rightleftharpoons \ce{H2O} \\[4pt] \ce{H_2O + H^+} &\rightleftharpoons \ce{H3O+} \\[4pt] \ce{NH_3 + H^+} &\rightleftharpoons \ce{NH4+} \\[4pt] \ce{S^{2-} + H^+} &\rightleftharpoons \ce{HS-} \\[4pt] \ce{CO_3^{2-} + H^+} &\rightleftharpoons \ce{HCO3-} \\[4pt] \ce{F^- + H^+} &\rightleftharpoons \ce{HF} \end{align*}\]

In these two sets of equations, the behaviors of acids as proton donors and bases as proton acceptors are represented in isolation. In reality, all acid-base reactions involve the transfer of protons between acids and bases. For example, consider the acid-base reaction that takes place when ammonia is dissolved in water. A water molecule (functioning as an acid) transfers a proton to an ammonia molecule (functioning as a base), yielding the conjugate base of water, \(\ce{OH^-}\), and the conjugate acid of ammonia, \(\ce{NH4+}\):

The reaction between a Brønsted-Lowry acid and water is called acid ionization. For example, when hydrogen fluoride dissolves in water and ionizes, protons are transferred from hydrogen fluoride molecules to water molecules, yielding hydronium ions and fluoride ions:

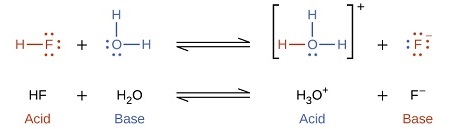
with

\[K =\dfrac{[\ce{H3O^{+}}][\ce{F^{-}}]}{[\ce{HF}]}\nonumber\]

When we add a base to water, a base ionization reaction occurs in which protons are transferred from water molecules to base molecules. For example, adding ammonia to water yields hydroxide ions and ammonium ions:

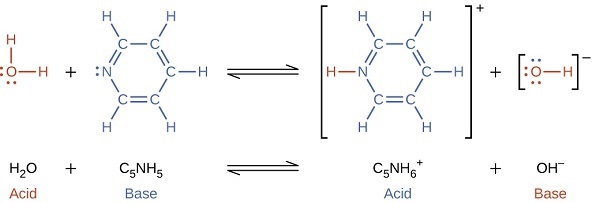
with

\[K =\dfrac{[\ce{C5NH6^{+}}][\ce{OH^{-}}]}{[\ce{C5NH5}]} \nonumber\]

Notice that both these ionization reactions are represented as equilibrium processes. The relative extent to which these acid and base ionization reactions proceed is an important topic treated in a later section of this chapter. In the preceding paragraphs we saw that water can function as either an acid or a base, depending on the nature of the solute dissolved in it. In fact, in pure water or in any aqueous solution, water acts both as an acid and a base. A very small fraction of water molecules donate protons to other water molecules to form hydronium ions and hydroxide ions:

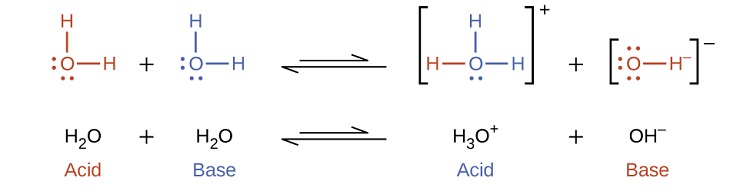
This type of reaction, in which a substance ionizes when one molecule of the substance reacts with another molecule of the same substance, is referred to as autoionization. Pure water undergoes autoionization to a very slight extent. Only about two out of every \(10^9\) molecules in a sample of pure water are ionized at 25 °C. The equilibrium constant for the ionization of water is called the ion-product constant for water (\(K_w\)):

\[\ce{H_2O(l) + H2O(l) <=> H_3O^{+}(aq) + OH^{-}(aq)} \]

with

\[K_\ce{w}=\ce{[H_3O^+][OH^- ]} \label{15.1.4}\]

The slight ionization of pure water is reflected in the small value of the equilibrium constant; at 25 °C, \(K_w\) has a value of \(1.0 \times 10^{−14}\). The process is endothermic, and so the extent of ionization and the resulting concentrations of hydronium ion and hydroxide ion increase with temperature. For example, at 100 °C, the value for \(K_\ce{w}\) is approximately \(5.1 \times 10^{−13}\), roughly 100-times larger than the value at 25 °C.

Example \(\PageIndex{1}\): Ion Concentrations in Pure Water

What are the hydronium ion concentration and the hydroxide ion concentration in pure water at 25 °C?

Solution

The autoionization of water yields the same number of hydronium and hydroxide ions. Therefore, in pure water, \(\ce{[H_3O^+]} = \ce{[OH^- ]}\). At 25 °C:

\[\begin{align*} K_\ce{w} &=\ce{[H_3O^+][OH^- ]} \\[4pt] &= [\ce{H3O^{+}}]^2 \\[4pt] &= [\ce{OH^{-}} ]^2 \\[4pt] &=1.0 \times 10^{−14} \end{align*}\]

So

\[\ce{[H_3O^+]}=\ce{[OH^- ]}=\sqrt{1.0 \times 10^{−14}} =1.0 \times 10^{−7}\; M \nonumber\]

The hydronium ion concentration and the hydroxide ion concentration are the same, and we find that both equal \(1.0 \times 10^{−7}\; M\).

Exercise \(\PageIndex{1}\)

The ion product of water at 80 °C is \(2.4 \times 10^{−13}\). What are the concentrations of hydronium and hydroxide ions in pure water at 80 °C?

Answer

\[\ce{[H_3O^+]} = \ce{[OH^- ]} = 4.9 \times 10^{−7} \; M\nonumber\]

It is important to realize that the autoionization equilibrium for water is established in all aqueous solutions. Adding an acid or base to water will not change the position of the equilibrium. Example \( \PageIndex{2}\) demonstrates the quantitative aspects of this relation between hydronium and hydroxide ion concentrations.

Example \( \PageIndex{2}\): The Inverse Proportionality of \(\ce{[H_3O^+]}\) and \(\ce{[OH^- ]}\)

The Inverse Proportionality of [H₃O⁺] and [OH^-] A solution of carbon dioxide in water has a hydronium ion concentration of \(2.0 \times 10^{−6}\; M\). What is the concentration of hydroxide ion at 25 °C?

Solution

We know the value of the ion-product constant for water at 25 °C:

\[\ce{2 H_2O}_{(l)} \rightleftharpoons \ce{H_3O^+}_{(aq)} + \ce{OH^-}_{(aq)} \nonumber\]

\[K_\ce{w}=\ce{[H3O+][OH^- ]}=1.0 \times 10^{−14} \nonumber\]

Thus, we can calculate the missing equilibrium concentration.

Rearrangement of the K_w expression yields that \([\ce{OH^- }]\) is directly proportional to the inverse of [H₃O⁺]:

\[[\ce{OH^- }]=\dfrac{K_{\ce w}}{[\ce{H_3O^+}]}=\dfrac{1.0 \times 10^{−14}}{2.0 \times 10^{−6}}=5.0 \times 10^{−9} \nonumber\]

The hydroxide ion concentration in water is reduced to \(5.0 \times 10^{−9}\: M\) as the hydrogen ion concentration increases to \(2.0 \times 10^{−6}\; M\). This is expected from Le Chatelier’s principle; the autoionization reaction shifts to the left to reduce the stress of the increased hydronium ion concentration and the \(\ce{[OH^- ]}\) is reduced relative to that in pure water.

A check of these concentrations confirms that our arithmetic is correct:

\[K_\ce{w}=\ce{[H_3O^+][OH^- ]}=(2.0 \times 10^{−6})(5.0 \times 10^{−9})=1.0 \times 10^{−14} \nonumber\]

Exercise \(\PageIndex{2}\)

What is the hydronium ion concentration in an aqueous solution with a hydroxide ion concentration of 0.001 M at 25 °C?

Answer

\[\ce{[H3O+]} = 1 \times 10^{−11} M \nonumber\]

Amphoteric Species

Like water, many molecules and ions may either gain or lose a proton under the appropriate conditions. Such species are said to be amphiprotic. Another term used to describe such species is amphoteric, which is a more general term for a species that may act either as an acid or a base by any definition (not just the Brønsted-Lowry one). Consider for example the bicarbonate ion, which may either donate or accept a proton as shown here:

\[\ce{HCO^-3(aq) + H2O(l) <=> CO^{2-}3(aq) + H3O^+(aq)} \nonumber\]

\[ \ce{HCO^{-}3(aq) + H2O(l) <=> H2CO3(aq) + OH^{-}(aq)} \nonumber\]

Example \(\PageIndex{3}\): The Acid-Base Behavior of an Amphoteric Substance

Write separate equations representing the reaction of \(\ce{HSO3-}\)

1. as an acid with \(\ce{OH^-}\)
2. as a base with HI

Solution

1. \(\ce{HSO3-}(aq)+ \ce{OH^-}(aq)\rightleftharpoons \ce{SO3^2-}(aq)+ \ce{H_2O}_{(l)} \)
2. \(\ce{HSO3-}(aq)+\ce{HI}(aq)\rightleftharpoons \ce{H2SO3}(aq)+\ce{I-}(aq)\)

Exercise \(\PageIndex{3}\)

Write separate equations representing the reaction of \(\ce{H2PO4-}\)

1. as a base with HBr
2. as an acid with \(\ce{OH^-}\)

Answer a

\(\ce{H2PO4-}(aq)+\ce{HBr}(aq)\rightleftharpoons \ce{H3PO4}(aq)+\ce{Br-}(aq)\)

Answer b

\(\ce{H2PO4-}(aq)+\ce{OH^-} (aq)\rightleftharpoons \ce{HPO4^2-}(aq)+ \ce{H_2O}_{(l)} \)

Lewis Acids and Bases

The Brønsted-Lowry proton donor-acceptor concept has been one of the most successful theories of Chemistry. But as with any such theory, it is fair to ask if this is not just a special case of a more general theory that could encompass an even broader range of chemical science. In 1916, G.N. Lewis of the University of California proposed that the electron pair is the dominant actor in acid-base chemistry. The Lewis theory did not become very well known until about 1923 (the same year that Brønsted and Lowry published their work), but since then it has been recognized as a very powerful tool for describing chemical reactions of widely different kinds and is widely used in organic and inorganic chemistry. The Brønsted–Lowry concept of acids and bases defines a base as any species that can accept a proton, and an acid as any substance that can donate a proton. Lewis proposed an alternative definition that focuses on pairs of electrons instead. According to Lewis:

• An acid is a substance that accepts a pair of electrons, and in doing so, forms a covalent bond with the entity that supplies the electrons.
• A base is a substance that donates an unshared pair of electrons to a recipient species with which the electrons can be shared.

In modern chemistry, electron donors are often referred to as nucleophiles, while acceptors are electrophiles.

Lewis Acid-Base Neutralization Involving Electron-Pair Transfer

Just as any Arrhenius acid is also a Brønsted acid, any Brønsted acid is also a Lewis acid, so the various acid-base concepts are all "upward compatible". Although we do not really need to think about electron-pair transfers when we deal with ordinary aqueous-solution acid-base reactions, it is important to understand that it is the opportunity for electron-pair sharing that enables proton transfer to take place.

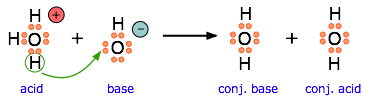
This equation for a simple acid-base neutralization shows how the Brønsted and Lewis definitions are really just different views of the same process. Take special note of the following points:

• The arrow shows the movement of a proton from the hydronium ion to the hydroxide ion.
• Note that the electron-pairs themselves do not move; they remain attached to their central atoms. The electron pair on the base is "donated" to the acceptor (the proton) only in the sense that it ends up being shared with the acceptor, rather than being the exclusive property of the oxygen atom in the hydroxide ion.
• Although the hydronium ion is the nominal Lewis acid here, it does not itself accept an electron pair, but acts merely as the source of the proton that coordinates with the Lewis base.

Note

The point about the electron-pair remaining on the donor species is especially important to bear in mind. For one thing, it distinguishes a Lewis acid-base reaction from an oxidation-reduction reaction, in which a physical transfer of one or more electrons from donor to acceptor does occur.

The product of a Lewis acid-base reaction is known formally as an "adduct" or "complex", although we do not ordinarily use these terms for simple proton-transfer reactions such as the one in the above example. Here, the proton combines with the hydroxide ion to form the "adduct" \(\ce{H2O}\). The following examples illustrate these points for some other proton-transfer reactions that you should already be familiar with.

Another example, showing the autoprotolysis of water. Note that the conjugate acid is also the adduct.

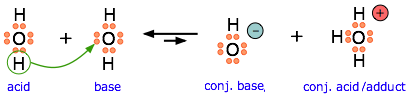
Ammonia is both a Brønsted and a Lewis base, owing to the unshared electron pair on the nitrogen. The reverse of this reaction represents the hydrolysis of the ammonium ion.

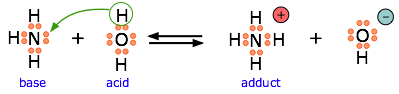
Because \(\ce{HF}\) is a weak acid, fluoride salts behave as bases in aqueous solution. As a Lewis base, \(\ce{F^{–}}\) accepts a proton from water, which is transformed into a hydroxide ion.

The bisulfite ion is amphiprotic and can act as an electron donor or acceptor.

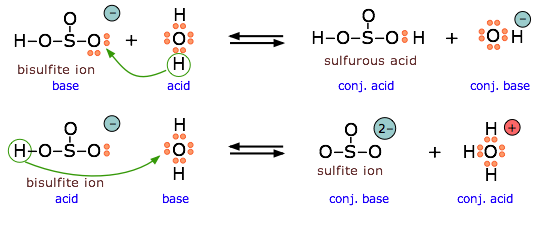
All Brønsted–Lowry bases (proton acceptors), such as \(\ce{OH^{−}}\), \(\ce{H2O}\), and \(\ce{NH3}\), are also electron-pair donors. Thus the Lewis definition of acids and bases does not contradict the Brønsted–Lowry definition. Rather, it expands the definition of acids to include substances other than the \(\ce{H^{+}}\) ion.

Lewis Acid-Base Neutralization without Transferring Protons

Electron-deficient molecules, such as BCl₃, contain less than an octet of electrons around one atom and have a strong tendency to gain an additional pair of electrons by reacting with substances that possess a lone pair of electrons. Lewis’s definition, which is less restrictive than either the Brønsted–Lowry or the Arrhenius definition, grew out of his observation of this tendency. A general Brønsted–Lowry acid–base reaction can be depicted in Lewis electron symbols as follows:

The proton (H⁺), which has no valence electrons, is a Lewis acid because it accepts a lone pair of electrons on the base to form a bond. The proton, however, is just one of many electron-deficient species that are known to react with bases. For example, neutral compounds of boron, aluminum, and the other Group 13 elements, which possess only six valence electrons, have a very strong tendency to gain an additional electron pair. Such compounds are therefore potent Lewis acids that react with an electron-pair donor such as ammonia to form an acid–base adduct, a new covalent bond, as shown here for boron trifluoride (BF₃):

The bond formed between a Lewis acid and a Lewis base is a coordinate covalent bond because both electrons are provided by only one of the atoms (N, in the case of F₃B:NH₃). After it is formed, however, a coordinate covalent bond behaves like any other covalent single bond.

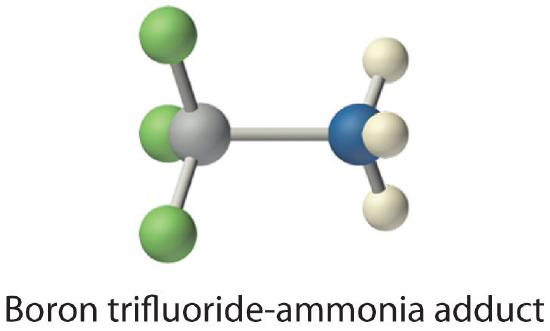
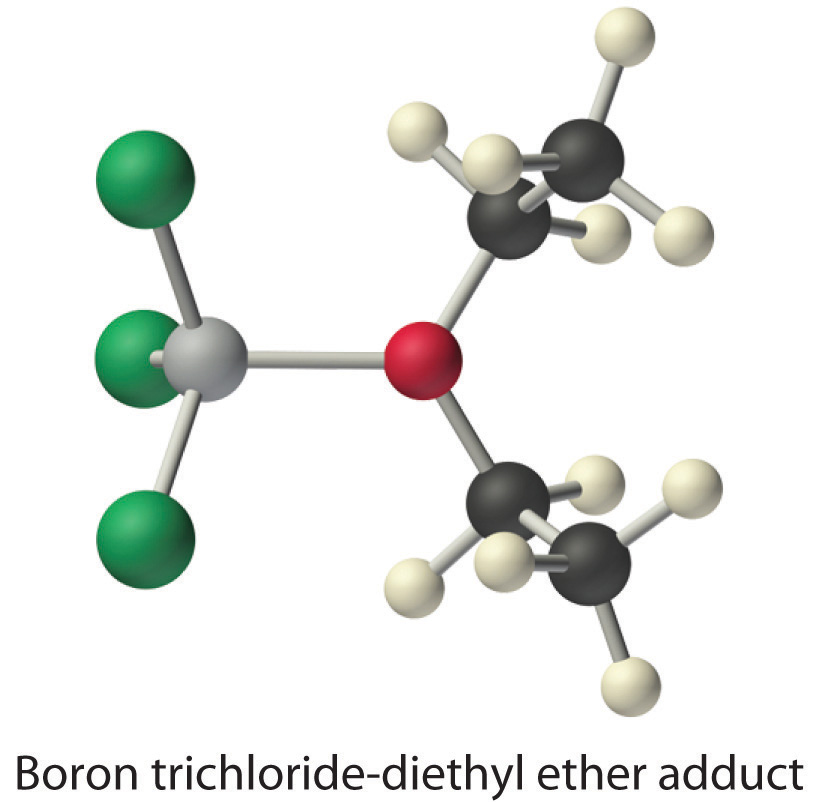
Species that are very weak Brønsted–Lowry bases can be relatively strong Lewis bases. For example, many of the group 13 trihalides are highly soluble in ethers (R–O–R′) because the oxygen atom in the ether contains two lone pairs of electrons, just as in H₂O. Hence the predominant species in solutions of electron-deficient trihalides in ether solvents is a Lewis acid–base adduct. A reaction of this type is shown in Figure \(\PageIndex{1}\) for boron trichloride and diethyl ether:

Figure \(\PageIndex{1}\): Lewis Acid/Base reaction of boron trichloride and diethyl ether reaction

Note

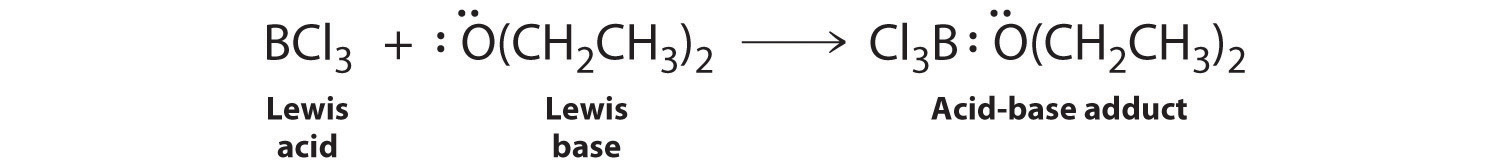
• Electron-deficient molecules (those with less than an octet of electrons) are Lewis acids.
• The acid-base behavior of many compounds can be explained by their Lewis electron structures.

Many molecules with multiple bonds can act as Lewis acids. In these cases, the Lewis base typically donates a pair of electrons to form a bond to the central atom of the molecule, while a pair of electrons displaced from the multiple bond becomes a lone pair on a terminal atom.

Figure \(\PageIndex{2}\): The highly electronegative oxygen atoms pull electron density away from carbon, so the carbon atom acts as a Lewis acid. Arrows indicate the direction of electron flow.

Figure \(\PageIndex{2}\): Lewis Acid/Base reaction of the hydroxide ion with carbon dioxide

Example \(\PageIndex{4}\)

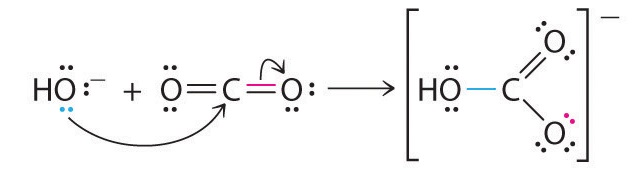
Identify the acid and the base in each Lewis acid–base reaction.

1. BH₃ + (CH₃)₂S → H₃B:S(CH₃)₂
2. CaO + CO₂ → CaCO₃
3. BeCl₂ + 2 Cl⁻ → BeCl₄²⁻

Given: reactants and products

Asked for: identity of Lewis acid and Lewis base

Strategy:

In each equation, identify the reactant that is electron deficient and the reactant that is an electron-pair donor. The electron-deficient compound is the Lewis acid, whereas the other is the Lewis base.

Solution:

1. In BH₃, boron has only six valence electrons. It is therefore electron deficient and can accept a lone pair. Like oxygen, the sulfur atom in (CH₃)₂S has two lone pairs. Thus (CH₃)₂S donates an electron pair on sulfur to the boron atom of BH₃. The Lewis base is (CH₃)₂S, and the Lewis acid is BH₃.
2. As in the reaction shown in Equation 8.21, CO₂ accepts a pair of electrons from the O²⁻ ion in CaO to form the carbonate ion. The oxygen in CaO is an electron-pair donor, so CaO is the Lewis base. Carbon accepts a pair of electrons, so CO₂ is the Lewis acid.
3. The chloride ion contains four lone pairs. In this reaction, each chloride ion donates one lone pair to BeCl₂, which has only four electrons around Be. Thus the chloride ions are Lewis bases, and BeCl₂ is the Lewis acid.

Exercise \(\PageIndex{4A}\)

Identify the acid and the base in each Lewis acid–base reaction.

1. (CH₃)₂O + BF₃ → (CH₃)₂O:BF₃
2. H₂O + SO₃ → H₂SO₄

Answer a

Lewis base: (CH₃)₂O; Lewis acid: BF₃

Answer b

Lewis base: H₂O; Lewis acid: SO₃

Exercise \(\PageIndex{4B}\)

Here are several more examples of Lewis acid-base reactions that cannot be accommodated within the Brønsted or Arrhenius models. Identify the Lewis acid and Lewis base in each reaction.

1. \(Al(OH)_3 + OH^– \rightarrow Al(OH)_4^–\)
2. \(SnS_2 + S^{2–} \rightarrow SnS_3^{2–}\)
3. \(Cd(CN)_2 + 2 CN^– \rightarrow Cd(CN)_4^{2+}\)
4. \(AgCl + 2 NH_3 \rightarrow Ag(NH_3)_2^+ + Cl^–\)
5. \(Fe^{2+} + NO \rightarrow Fe(NO)^{2+}\)
6. \([Ni^{2+} + 6 NH_3 \rightarrow Ni(NH_3)_5^{2+}\)

Video \(\PageIndex{1}\): Overview of Lewis Acids and Bases

Summary

A compound that can donate a proton (a hydrogen ion) to another compound is called a Brønsted-Lowry acid. The compound that accepts the proton is called a Brønsted-Lowry base. The species remaining after a Brønsted-Lowry acid has lost a proton is the conjugate base of the acid. The species formed when a Brønsted-Lowry base gains a proton is the conjugate acid of the base. Thus, an acid-base reaction occurs when a proton is transferred from an acid to a base, with formation of the conjugate base of the reactant acid and formation of the conjugate acid of the reactant base. Amphiprotic species can act as both proton donors and proton acceptors. Water is the most important amphiprotic species. It can form both the hydronium ion, H₃O⁺, and the hydroxide ion, \(\ce{OH^-}\) when it undergoes autoionization:

\[\ce{2 H_2O}_{(l)} \rightleftharpoons \ce{H_3O^+}(aq)+\ce{OH^-} (aq) \nonumber\]

The ion product of water, K_w is the equilibrium constant for the autoionization reaction:

\[K_\ce{w}=\mathrm{[H_3O^+][OH^- ]=1.0 \times 10^{−14} \; at\; 25°C} \nonumber\]

Glossary

acid ionization

reaction involving the transfer of a proton from an acid to water, yielding hydronium ions and the conjugate base of the acid

amphiprotic

species that may either gain or lose a proton in a reaction

amphoteric

species that can act as either an acid or a base

autoionization

reaction between identical species yielding ionic products; for water, this reaction involves transfer of protons to yield hydronium and hydroxide ions

base ionization

reaction involving the transfer of a proton from water to a base, yielding hydroxide ions and the conjugate acid of the base

Brønsted-Lowry acid

proton donor

Brønsted-Lowry base

proton acceptor

conjugate acid

substance formed when a base gains a proton

conjugate base

substance formed when an acid loses a proton

ion-product constant for water (K_w)

equilibrium constant for the autoionization of water

Contributors and Attributions

• Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).