24.9: Acid-Base Reactions of Complex Ions
- Page ID
- 24358
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The pH's of solutions containing hexaaqua ions vary a lot from one metal to another (assuming you are comparing solutions of equal concentrations). However, the underlying explanation is the same for all of them. Consider the hexaaquairon(III) ion, \([Fe(H_2O)_6]^{3+}\) with six water molecules are attached to the central iron(III) ion via a co-ordinate bond using one of the lone pairs on the oxygen. Imagine for the moment that the 3+ charge is located entirely on the iron.
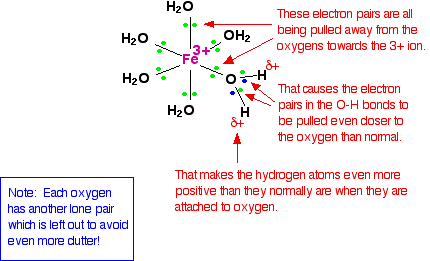
When the lone pairs on the oxygen atoms form co-ordinate bonds with the iron, there is obviously a movement of electrons towards the iron. That has an effect on the electrons in the O-H bonds. These electrons, in turn, get pulled towards the oxygen even more than usual. That leaves the hydrogen nuclei more exposed than normal. The overall effect is that each of the hydrogen atoms is more positive than it is in ordinary water molecules. The 3+ charge is no longer located entirely on the iron, but spreads out over the whole ion - much of it on the hydrogen atoms.
The 3+ charge is no longer located entirely on the iron, but spreads out over the whole ion - much of it on the hydrogen atoms.
The hydrogen atoms attached to the water ligands are sufficiently positive that they can be pulled off in a reaction involving water molecules in the solution. The first stage of this process is:
\[Fe(H_2O)_6]^{3+} + H_2O \rightleftharpoons [Fe(H_2O)_5(OH)]^{2+} _{(aq)} + H_3O^+_{(aq)} \label{Eqa1}\]
The complex ion is acting as an acid by donating a hydrogen ion to water molecules in the solution. The water is, of course, acting as a base by accepting the hydrogen ion. Because of the confusing presence of water from two different sources (the ligands and the solution), it is easier to simplify Equation \(\ref{Eqa1}\):
\[ [Fe(H_2O)_6]^{3+} _{(aq)} \rightleftharpoons [Fe(H_2O)_5(OH)]^{2+} _{(aq)} + H^+ _{(aq)} \]
However, if you write it like this, remember that the hydrogen ion is not just falling off the complex ion. It is being pulled off by a water molecule in the solution. The hexaaquairon(III) ion is quite strongly acidic giving solutions with pH's around 1.5, depending on concentration. You can get further loss of hydrogen ions as well, from a second and a third water molecule.
Losing a second hydrogen ion:
\[ [ Fe(H_2O)_5(OH)]^{2+} _{(aq)} \rightleftharpoons [ Fe(H_2O)_4(OH)_2]^{+} _{(aq)} + H^+ _{(aq)} \]
. . . and a third one:
\[ [ Fe(H_2O)_4(OH)_2]^{+} _{(aq)} \rightleftharpoons [ Fe(H_2O)_3(OH)_4] _{(s)} + H^+ _{(aq)} \]
This time you end up with a neutral \([ Fe(H_2O)_3(OH)_4]_{(s)}\) complex t hat is weakly soluble in water and precipitates.
Video \(\PageIndex{1}\): Combining solutions of sodium hydroxide and iron(III) nitrate produces a precipitate of iron(III) hydroxide. The precipitate can be dissolved by adding a small volume of hydrochloric acid. The precipitate reappears when the sodium hydroxide solution is added again. https://www.youtube.com/watch?v=asdDyWmE9KQ
Exerimental Perspective
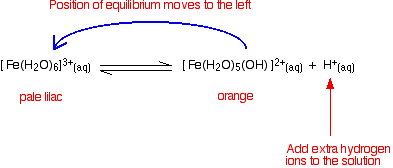
Looking at the equilibrium showing the loss of the first hydrogen ion (Equation \(\ref{Eqa1}\)):
![]()
The color of the new complex ion on the right-hand side is so strong that it completely masks the color of the hexaaqua ion. In concentrated solutions, the equilibrium position will be even further to the right-hand side (Le Chatelier's Principle), and so the color darkens. You will also get significant loss of other hydrogen ions leading to some formation of the neutral complex - and so you get some precipitate. The position of this equilibrium can be shifted by adding extra hydrogen ions from a concentrated acid (e.g., by increasing pH by adding concentrated acid to the solution (Video \(\PageIndex{1}\)). The new hydrogen ions push the position of the equilibrium to the left so that you can see the color of the hexaaqua ion:
Solutions containing 3+ hexaaqua ions tend to have pH's in the range from 1 to 3. Solutions containing 2+ ions have higher pH's - typically around 5 - 6, although they can go down to about 3. Remember that the reason that these ions are acidic is because of the pull of the electrons towards the positive central ion. An ion with 3+ charges on it is going to pull the electrons more strongly than one with only 2+ charges.
In 3+ ions, the electrons in the O-H bonds will be pulled further away from the hydrogens than in 2+ ions. That means that the hydrogen atoms in the ligand water molecules will have a greater positive charge in a 3+ ion, and so will be more attracted to water molecules in the solution. If they are more attracted, they will be more readily lost - and so the 3+ ions are more acidic.
If you have ions of the same charge, it seems reasonable that the smaller the volume this charge is packed into, the greater the distorting effect on the electrons in the O-H bonds. Ions with the same charge but in a smaller volume (a higher charge density) would be expected to be more acidic. You would therefore expect to find that the smaller the radius of the metal ion, the stronger the acid. Unfortunately, it's not that simple!
Summary
There probably is a relationship between ionic radius and acid strength, but that it is nothing like as simple and straightforward as most books at this level pretend. The problem is that there are other more important effects operating as well (quite apart from differences in charge) and these can completely swamp the effect of the changes in ionic radius. You have to look in far more detail at the bonding in the hexaaqua ions and the product ions

