18.4: Limitations of the Kₛₚ Concept
- Page ID
- 24308
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Solubility equilibria defined by a single, simple Ks expression are probably the exception rather than the rule. Such equilibria are often in competition with other reactions with such species as H+or OH–, complexing agents, oxidation-reduction, formation of other sparingly soluble species or, in the case of carbonates and sulfites, of gaseous products. The exact treatments of these systems can be extremely complicated, involving the solution of large sets of simultaneous equations. For most practical purposes it is sufficient to recognize the general trends, and to carry out approximate calculations.
The solubility product of an ionic compound describes the concentrations of ions in equilibrium with a solid, but what happens if some of the cations become associated with anions rather than being completely surrounded by solvent? Then predictions of the total solubility of the compound based on the assumption that the solute exists solely as discrete ions would differ substantially from the actual solubility, as would predictions of ionic concentrations. In general, four situations explain why the solubility of a compound may be other than expected: ion pair formation, the incomplete dissociation of molecular solutes, the formation of complex ions, and changes in pH.
The Diverse Ion Effect (The Salt Effect)
A sparingly-soluble salt will be more soluble in a solution that contains non-participating ions. This is just the opposite of the common ion effect, and it might at first seem rather counter-intuitive: why would adding more ions of any kind make a salt more likely to dissolve?
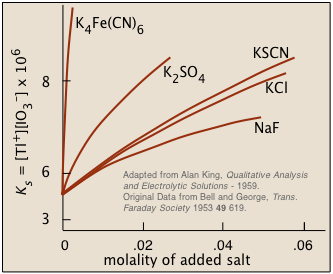
Although the concentrations of ions in equilibrium with a sparingly soluble solid are so low that they are essentially the same as the activities, the presence of other ions at concentrations of about 0.001 M or greater can materially reduce the activities of the dissolution products, permitting the solubilities to be greater than what simple equilibrium calculations would predict.
The Diverse Ion Effect typically has the opposite effect on solubility than the common ion effect.
The higher the charge of the foreign ion, the more pronounced is the salt effect. This tells us that inter-ionic (and thus electrostatic) interactions must play a role. The details are rather complicated, but the general idea is that all ions in solution, besides possessing tightly-held waters of hydration, tend to attract oppositely-charged ions ("counter-ions") around them. This "atmosphere" of counterions is always rather diffuse, but much less so (and more tightly bound) when one or both kinds of ions have greater charges. From a distance, these ion-counterion pairs (or ion pairs) bodies appear to be almost electrically neutral, which keeps them from interacting with each other (as to form a precipitate).
How does the solubility of \(AgCl\) change in absence and presence of \(NaNO_3\), given that the molar solubility product of \(AgCl\) is \(1.76 \times 10^{−10}\).
Solution
The Uncommon Ion Effect is a "real" effect and requires the activity definition of \(K_{sp}\) to address. The exact definition of the solubility constant is:
\[K_{sp}=a\{Ag^+\} \cdot a\{Cl^−\}=[Ag+] \gamma(Ag^+) [Cl^−] \gamma (Cl^−) \nonumber\]
Where \(a\{Ag^+\}\) and \(a\{Cl^−\}\) are the activities of these ions in the presence of the \(NaNO_3\). The \(\gamma\) values are the are the corresponding activity coefficients for the ions.
- In dilute solutions (i.e. absence of \(NaNO_3\)\) \[ \gamma (Ag^+)= \gamma (Cl^−)=1 \nonumber\] So, the solubility of \(AgCl\) is then \[[Ag^+]=\sqrt{K_{sp}} =1.33 \times 10^{−5}\]
- In the presence of \(NaNO_3\), the activity coefficients deviate from unity. So \[[Ag^+] = \dfrac{\sqrt{K_{sp}}}{ \sqrt{\gamma(Ag^+)\gamma (Cl^−) }}\]. The denominator has to evaluated from an activity table and is 0.769 so \([Ag^+] = \dfrac{\sqrt{K_{sp}}}{0.769} = 1.73 \times 10^{-5}\].
Hence, in the presence of the \(NaNO_3\) soluble salt, the molar solubility of the slightly soluble \(AgCl\) salt increases. An opposite effect is expected if there were a common ions between the two salts.
Incomplete Dissociation of Solutes into Ions
An ion pair consists of a cation and an anion that are in intimate contact in solution, rather than separated by solvent (Figure \(\PageIndex{1}\)). The ions in an ion pair are held together by the same attractive electrostatic force in ionic solids. As a result, the ions in an ion pair migrate as a single unit, whose net charge is the sum of the charges on the ions. In many ways, we can view an ion pair as a species intermediate between the ionic solid (in which each ion participates in many cation–anion interactions that hold the ions in a rigid array) and the completely dissociated ions in solution (where each is fully surrounded by water molecules and free to migrate independently).
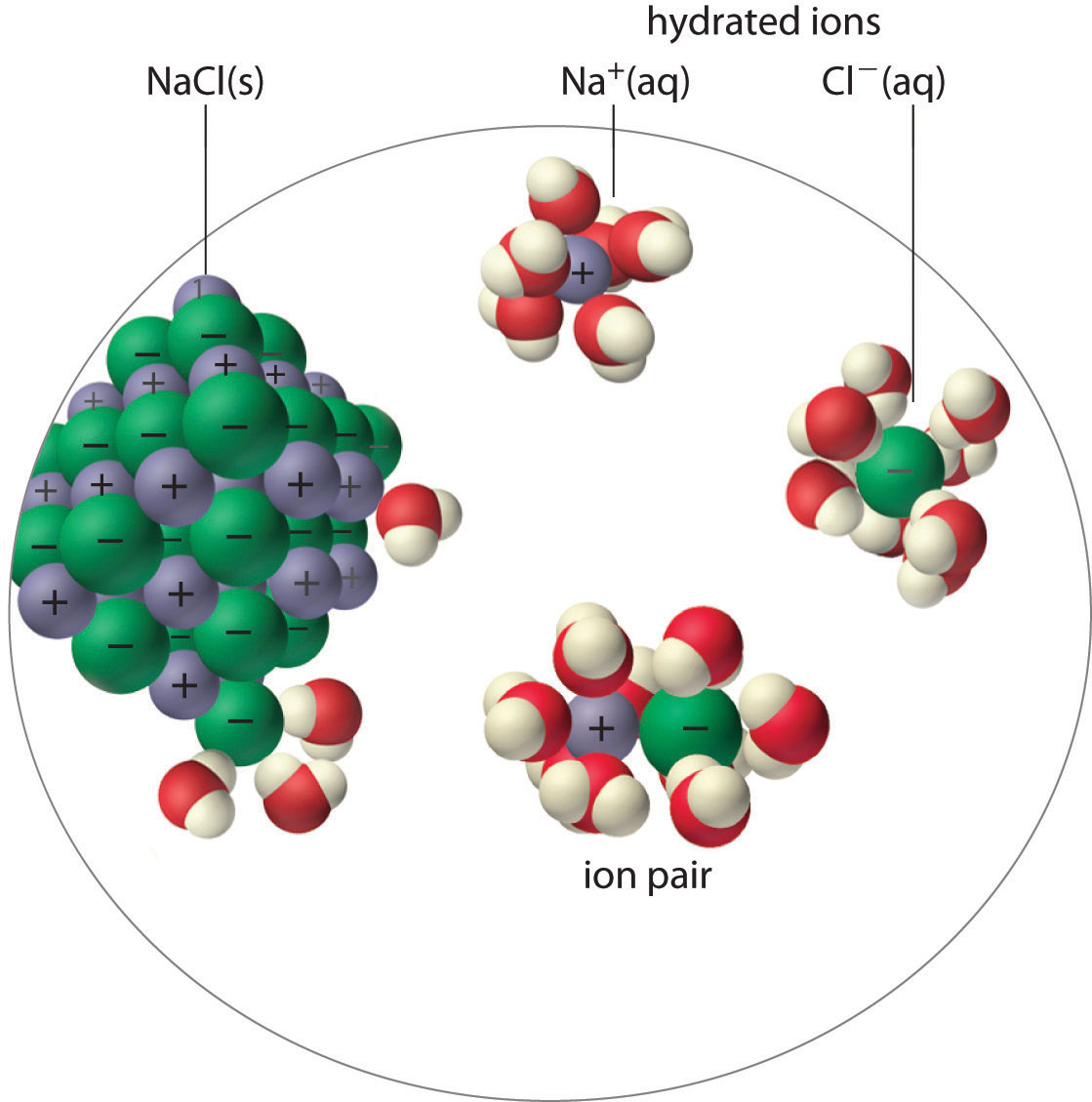
The overall effect is to reduce the concentrations of the less-shielded ions that are available to combine to form a precipitate. We say that the thermodynamically-effective concentrations of these ions are less than their "analytical" concentrations. Chemists refer to these effective concentrations as ionic activities, and they denote them by curly brackets {Ag+} as opposed to square brackets [Ag+] which refer to the nominal or analytical concentrations.
As illustrated for calcium sulfate in the following equation, a second equilibrium must be included to describe the solubility of salts that form ion pairs:
\[\mathrm{CaSO_4(s)}\rightleftharpoons\mathrm{Ca^{2+}}\cdot\underset{\textrm{ion pair}}{\mathrm{SO_4^{2-}(aq)}}\rightleftharpoons \mathrm{Ca^{2+}(aq)}+\mathrm{SO_4^{2-}(aq)} \label{17.5.3.1}\]
The ion pair is represented by the symbols of the individual ions separated by a dot, which indicates that they are associated in solution. The formation of an ion pair is a dynamic process, just like any other equilibrium, so a particular ion pair may exist only briefly before dissociating into the free ions, each of which may later associate briefly with other ions.
Ion-pair formation can have a major effect on the measured solubility of a salt. For example, the measured Ksp for calcium sulfate is 4.93 × 10−5 at 25°C. The solubility of CaSO4 should be 7.02 × 10−3 M if the only equilibrium involved were as follows:
\[CaSO_{4(s)} \rightleftharpoons Ca^{2+}_{(aq)} + SO^{2−}_{4(aq)} \label{17.5.2}\]
In fact, the experimentally measured solubility of calcium sulfate at 25°C is 1.6 × 10−2 M, almost twice the value predicted from its Ksp. The reason for the discrepancy is that the concentration of ion pairs in a saturated CaSO4 solution is almost as high as the concentration of the hydrated ions. Recall that the magnitude of attractive electrostatic interactions is greatest for small, highly charged ions. Hence ion pair formation is most important for salts that contain M2+ and M3+ ions, such as Ca2+ and La3+, and is relatively unimportant for salts that contain monopositive cations, except for the smallest, Li+. We therefore expect a saturated solution of CaSO4 to contain a high concentration of ion pairs and its solubility to be greater than predicted from its Ksp.
Simultaneous Equilibria (Side Reactions)
A molecular solute may also be more soluble than predicted by the measured concentrations of ions in solution due to incomplete dissociation. This is particularly common with weak organic acids. Although strong acids (HA) dissociate completely into their constituent ions (H+ and A−) in water, weak acids such as carboxylic acids do not (Ka = 1.5 × 10−5). However, the molecular (undissociated) form of a weak acid (HA) is often quite soluble in water; for example, acetic acid (CH3CO2H) is completely miscible with water. Many carboxylic acids, however, have only limited solubility in water, such as benzoic acid (C6H5CO2H), with Ka = 6.25 × 10−5. Just as with calcium sulfate, we need to include an additional equilibrium to describe the solubility of benzoic acid:
\[ C_6H_5CO_2H_{(s)} \rightleftharpoons C_6H_5CO_2H_{(aq)} \rightleftharpoons C_6H_5CO^−_{2(aq)} + H^+_{(aq)} \label{17.5.3}\]
In a case like this, measuring only the concentration of the ions grossly underestimates the total concentration of the organic acid in solution. In the case of benzoic acid, for example, the pH of a saturated solution at 25°C is 2.85, corresponding to [H+] = [C6H5CO2−] = 1.4 × 10−3 M. The total concentration of benzoic acid in the solution, however, is 2.8 × 10−2 M. Thus approximately 95% of the benzoic acid in solution is in the form of hydrated neutral molecules—\(C_6H_5CO_2H_{(aq)}\)—and only about 5% is present as the dissociated ions (Figure \(\PageIndex{3}\)).
Incomplete dissociation of a molecular solute that is miscible with water can increase the solubility of the solute.
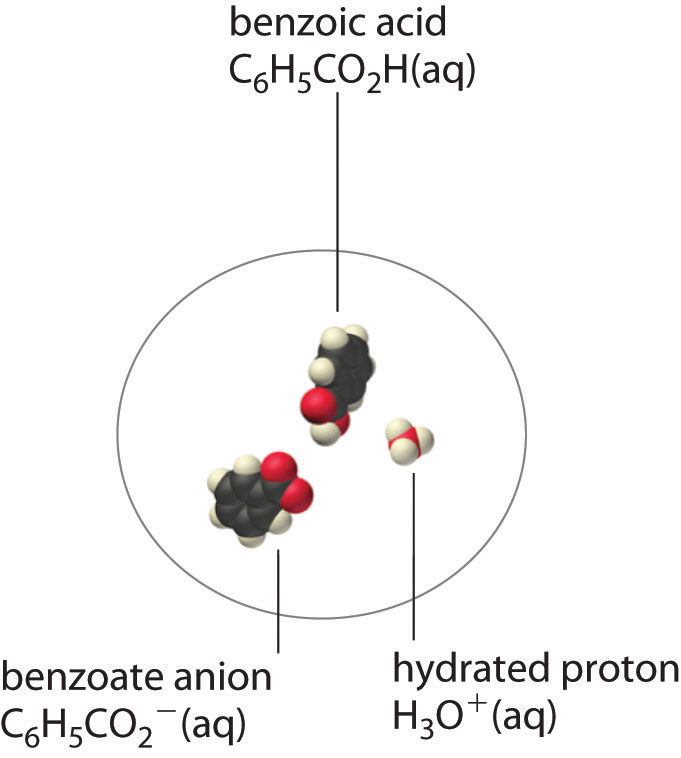
Although ion pairs, such as Ca2+•SO42−, and undissociated electrolytes, such as C6H5CO2H, are both electrically neutral, there is a major difference in the forces responsible for their formation. Simple electrostatic attractive forces between the cation and the anion hold the ion pair together, whereas a polar covalent O−H bond holds together the undissociated electrolyte.
The dissolution of cadmium iodide is water is commonly represented as
\[CdI_{2(s)} \rightleftharpoons Cd^{2+} + 2 I^–\]
Firstly, they combine to form neutral, largely-covalent molecular species:
\[Cd^{2+}_{(aq)} + 2 I^–_{(aq)} → CdI_{2(aq)}\]
This non-ionic form accounts for 78% of the Cd present in the solution! In addition, they form a molecular ion \(CdI^–_{(aq)}\) according to the following scheme:
| \(CdI_{2(s)} \rightleftharpoons Cd^{2+} + 2 I^–\) | \(K_1 = 10^{–3.9}\) |
| \(Cd^{2+} + I^– \rightleftharpoons CdI^+\) | \(K_2= 10^{+2.3}\) |
| \(CdI2_{(s)} \rightleftharpoons CdI^++ I^–\) | \(K = 10^{–1.6} = 0.023\) |
As a consequence, the concentration of "free" Cd2+(aq) in an aqueous cadmium iodide solution is only about 2% of the value you would calculate by taking K1 as the solubility product. The principal component of such as solution is actually [covalently-bound] CdI2(aq). It turns out that
Many salts, especially those of metals beyond Group 2, are similarly only partially ionized in aqueous solution:
| salt | molarity | % cation | other species |
|---|---|---|---|
| KCl | 0.52 | 95 | KCl(aq) 5% |
| MgSO4 | 0.04 | 58 | MgSO4(aq) 42% |
| CaCl2 | 0.44 | 70 | CaCl+(aq) 30% |
| CuSO4 | 0.045 | 56 | CuSO4(aq) 44% |
| CdI2 | 0.50 | 2 | CdI2(aq) 76%, CdI–(aq) 22% |
| FeCl3 | 0.1 | 10 | FeCl2+(aq) 42%, FeCl2(aq) 40%, FeOH2+(aq) 6%, Fe(OH)2+(aq) 2% |
The data shown Tables \(\PageIndex{1}\) and \(\PageIndex{2}\) are taken from the article Salts are Mostly NOT Ionized by Stephen Hawkes: 1996 J Chem Educ. 73(5) 421-423. This fact was stated by Arrhenius in 1887, but has been largely ignored and is rarely mentioned in standard textbooks.
Summary
The solubility constant, as with all equilibrium constants, are properly defined in terms of effective concentrations (activities) and the use of true concentrations to approximate activities in equilibrium constants can often fail. As with all approximations, it is important to understand the conditions that it will fail. three examples are discussed. The salt effect refers to the fact that the presence of a salt which has no ion in common with the solute, has an effect on the ionic strength of the solution and hence on activity coefficients, so that the equilibrium constant, expressed as a concentration quotient, changes.
Contributors and Attributions
- Wikipedia
Stephen Lower, Professor Emeritus (Simon Fraser U.) Chem1 Virtual Textbook
- Yomen Atassi (via StackExchange)

