Balancing Redox Equations Using Oxidation States
To balance a redox equation using the oxidation state method, we conceptually separate the overall reaction into two parts: an oxidation—in which the atoms of one element lose electrons—and a reduction—in which the atoms of one element gain electrons. Consider, for example, the reaction of Cr2+(aq) with manganese dioxide (MnO2) in the presence of dilute acid. Equation 8.8.1 is the net ionic equation for this reaction before balancing; the oxidation state of each element in each species has been assigned using the procedure described in Section 7.5:
\( \begin{matrix}
+2 & +4 & +1 & +3 & +2 & +1\; \; \\
Cr^{2+}\left ( aq \right ) &+\; \; \; \; \; \; \; \;MnO_{2}\left ( aq \right ) &+\; \; H^{+}\left ( aq \right ) &\rightarrow\; Cr^{3+}\left ( aq \right ) &+\;Mn^{2+} \left ( aq \right ) &+\; \; \; H_{2}O\left ( l \right ) \\
& \; \; \; \; \; \; \;-2 & & & & \; \; \; \; -2
\end{matrix} \tag{8.8.1} \)
Notice that chromium is oxidized from the +2 to the +3 oxidation state, while manganese is reduced from the +4 to the +2 oxidation state. We can write an equation for this reaction that shows only the atoms that are oxidized and reduced:
\(Cr^{2+} + Mn^{4+} \rightarrow Cr^{3+} + Mn^{2+} \tag{8.8.2}\)
The oxidation can be written as
\(Cr^{2+} \rightarrow Cr^{3+} + e^- \tag{8.8.3}\)
and the reduction as
\(Mn^{4+} + 2e^- \rightarrow Mn^{2+} \tag{8.8.4}\)
For the overall chemical equation to be balanced, the number of electrons lost by the reductant must equal the number gained by the oxidant. We must therefore multiply the oxidation and the reduction equations by appropriate coefficients to give us the same number of electrons in both. In this example, we must multiply the oxidation equation by 2 to give
\(2Cr^{2+} \rightarrow 2Cr^{3+} + 2e^- \tag{8.8.5}\)
| Note the Patterns |
| In a balanced redox reaction, the number of electrons lost by the reductant equals the number of electrons gained by the oxidant. |
The number of electrons lost in the oxidation now equals the number of electrons gained in the reduction:
\(2Cr^{2+} \rightarrow 2Cr^{3+} + 2e^- \tag{8.8.6}\)
\( Mn^{4+} + 2e^- \rightarrow Mn^{2+} \)
We then add the equations for the oxidation and the reduction and cancel the electrons on both sides of the equation, using the actual chemical forms of the reactants and products:
\( \begin{matrix}
2Cr^{2+}\left ( aq \right ) & \rightarrow & 2Cr^{3+}\left ( aq \right )+\cancel{2e^{-}}\\
& & & \\
2Cr^{2+}\left ( aq \right )+\cancel{2e^{-}}& \rightarrow & Mn^{2+}\left ( aq \right )\\
& & & \\
2Cr^{2+}\left ( aq \right )+2Cr^{2+}\left ( aq \right )&\rightarrow & 2Cr^{3+}\left ( aq \right ) + Mn^{2+}\left ( aq \right )
\end{matrix} \tag{8.8.7}\)
Although the electrons cancel and the metal atoms are balanced, the total charge on the left side of the equation (+4) does not equal the charge on the right side (+8). Because the reaction is carried out in the presence of aqueous acid, we can add H+ as necessary to either side of the equation to balance the charge. By the same token, if the reaction were carried out in the presence of aqueous base, we could balance the charge by adding OH− as necessary to either side of the equation to balance the charges. In this case, adding four H+ ions to the left side of the equation gives
\(2Cr^{2+}(aq) + MnO_2(s) + 4H^+(aq) \rightarrow 2Cr^{3+}(aq) + Mn^{2+}(aq) \tag{8.8.8}\)
Although the charges are now balanced, we have two oxygen atoms on the left side of the equation and none on the right. We can balance the oxygen atoms without affecting the overall charge balance by adding H2O as necessary to either side of the equation. Here, we need to add two H2O molecules to the right side:
\(2Cr^{2+}(aq) + MnO_2(s) + 4H^+(aq) \rightarrow 2Cr^{3+}(aq) + Mn^{2+}(aq) + 2H_2O(l) \tag{8.8.9}\)
Although we did not explicitly balance the hydrogen atoms, we can see by inspection that the overall chemical equation is now balanced. All that remains is to check to make sure that we have not made a mistake. This procedure for balancing reactions is summarized in Table 8.8.1 and illustrated in Example 17.
Table 8.8.1 Procedure for Balancing Oxidation–Reduction Reactions by the Oxidation State Method
- Write the unbalanced chemical equation for the reaction, showing the reactants and the products.
- Assign oxidation states to all atoms in the reactants and the products (see Section 3.5 ) and determine which atoms change oxidation state.
- Write separate equations for oxidation and reduction, showing (a) the atom(s) that is (are) oxidized and reduced and (b) the number of electrons accepted or donated by each.
- Multiply the oxidation and reduction equations by appropriate coefficients so that both contain the same number of electrons.
- Write the oxidation and reduction equations showing the actual chemical forms of the reactants and the products, adjusting the coefficients as necessary to give the numbers of atoms in step 4.
- Add the two equations and cancel the electrons.
- Balance the charge by adding H+ or OH− ions as necessary for reactions in acidic or basic solution, respectively.
- Balance the oxygen atoms by adding H2O molecules to one side of the equation.
- Check to make sure that the equation is balanced in both atoms and total charges.
|
Example 17
Arsenic acid (H3AsO4) is a highly poisonous substance that was once used as a pesticide. The reaction of elemental zinc with arsenic acid in acidic solution yields arsine (AsH3, a highly toxic and unstable gas) and Zn2+(aq). Balance the equation for this reaction using oxidation states:
\(H_3AsO_4(aq) + Zn(s) \rightarrow AsH_3(g) + Zn^{2+}(aq) \)
Given: reactants and products in acidic solution
Asked for: balanced chemical equation using oxidation states
Strategy:
Follow the procedure given in Table 8.8.1 for balancing a redox equation using oxidation states. When you are done, be certain to check that the equation is balanced.
Solution:
- Write a chemical equation showing the reactants and the products. Because we are given this information, we can skip this step.
-
Assign oxidation states using the procedure described in Section 3.5 and determine which atoms change oxidation state. The oxidation state of arsenic in arsenic acid is +6, and the oxidation state of arsenic in arsine is −3. Conversely, the oxidation state of zinc in elemental zinc is 0, and the oxidation state of zinc in Zn2+(aq) is +2:
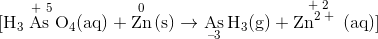.gif?revision=3&size=bestfit&width=350&height=36)
-
Write separate equations for oxidation and reduction. The arsenic atom in H3AsO4 is reduced from the +5 to the −3 oxidation state, which requires the addition of eight electrons:
\( Reduction \textrm: \: As^{5+} + 8e^- \rightarrow \underset{-3}{As ^{3-}}\)
Each zinc atom in elemental zinc is oxidized from 0 to +2, which requires the loss of two electrons per zinc atom:
\( Oxidation \textrm:\: Zn \rightarrow Zn^{2+} + 2e^- \)
-
Multiply the oxidation and reduction equations by appropriate coefficients so that both contain the same number of electrons. The reduction equation has eight electrons, and the oxidation equation has two electrons, so we need to multiply the oxidation equation by 4 to obtain
\(\begin{align} & Reduction\: (\times 1) \textrm : \: As^{5+} + 8e^- \rightarrow As^{3-} \\
& Oxidation\: (\times 4) \textrm : \: 4Zn^0 \rightarrow 4Zn^{2+} + 8e^- \end{align}\) -
Write the oxidation and reduction equations showing the actual chemical forms of the reactants and the products, adjusting coefficients as necessary to give the numbers of atoms shown in step 4. Inserting the actual chemical forms of arsenic and zinc and adjusting the coefficients gives
\(\begin{align} & Reduction \textrm : \: H_3AsO_4(aq) + 8e^- \rightarrow AsH_3(g) \\
& Oxidation \textrm : \: 4Zn(s) \rightarrow 4Zn^{2+}(aq) + 8e^- \end{align}\) -
Add the two equations and cancel the electrons. The sum of the two equations in step 5 is
\( H_3 AsO_4 (aq) + 4Zn(s) + \cancel{8e^-} \rightarrow AsH_3 (g) + 4Zn^{2+} (aq) + \cancel{8e^-} \) which then yields
\( H_3AsO_4(aq) + 4Zn(s) \rightarrow AsH_3(g) + 4Zn^{2+}(aq) \) -
Balance the charge by adding H+or OH−ions as necessary for reactions in acidic or basic solution, respectively. Because the reaction is carried out in acidic solution, we can add H+ ions to whichever side of the equation requires them to balance the charge. The overall charge on the left side is zero, and the total charge on the right side is 4 × (+2) = +8. Adding eight H+ ions to the left side gives a charge of +8 on both sides of the equation:
\(H_3AsO_4(aq) + 4Zn(s) + 8H^+(aq) \rightarrow AsH_3(g) + 4Zn^{2+}(aq) \) -
Balance the oxygen atoms by adding H2O molecules to one side of the equation. There are 4 O atoms on the left side of the equation. Adding 4 H2O molecules to the right side balances the O atoms:
\(H_3AsO_4(aq) + 4Zn(s) + 8H^+(aq) \rightarrow AsH_3(g) + 4Zn^{2+}(aq) + 4H_2O(l) \) Although we have not explicitly balanced H atoms, each side of the equation has 11 H atoms.
- Check to make sure that the equation is balanced in both atoms and total charges. To guard against careless errors, it is important to check that both the total number of atoms of each element and the total charges are the same on both sides of the equation:
\(\begin{align} & Atoms \textrm : \: 1As + 4Zn + 4O + 11H = 1As + 4Zn + 4O + 11H \\
& Total\: charge \textrm : \: 8(+1) = 4(+2) = +8 \end{align}\)
The balanced chemical equation for the reaction is therefore:
\(H_3AsO_4(aq) + 4Zn(s) + 8H^+(aq) \rightarrow AsH_3(g) + 4Zn^{2+}(aq) + 4H_2O(l) \)
Exercise
Copper commonly occurs as the sulfide mineral CuS. The first step in extracting copper from CuS is to dissolve the mineral in nitric acid, which oxidizes the sulfide to sulfate and reduces nitric acid to NO. Balance the equation for this reaction using oxidation states:
\(CuS(s) + H^+(aq) + NO_3^-(aq) \rightarrow Cu^{2+}(aq) + NO(g) + SO_4^{2-}(aq) \)
Answer: \(3CuS(s) + 8H^+(aq) + 8NO_3^-(aq) \rightarrow 3Cu^{2+}(aq) + 8NO(g) + 3SO_4^{2-}(aq) + 4H_2O(l)\)
Reactions in basic solutions are balanced in exactly the same manner. To make sure you understand the procedure, consider Example 18.
Example 18
The commercial solid drain cleaner, Drano, contains a mixture of sodium hydroxide and powdered aluminum. The sodium hydroxide dissolves in standing water to form a strongly basic solution, capable of slowly dissolving organic substances, such as hair, that may be clogging the drain. The aluminum dissolves in the strongly basic solution to produce bubbles of hydrogen gas that agitate the solution to help break up the clogs. The reaction is as follows:
\(Al(s) + H_2O(aq) \rightarrow [Al(OH)_4]^-(aq) + H_2(g) \)
Balance this equation using oxidation states.
Given: reactants and products in a basic solution
Asked for: balanced chemical equation
Strategy:
Follow the procedure given in Table 8.8.1 for balancing a redox reaction using oxidation states. When you are done, be certain to check that the equation is balanced.
Solution:
We will apply the same procedure used in Example 17 but in a more abbreviated form.
- The equation for the reaction is given, so we can skip this step.
-
The oxidation state of aluminum changes from 0 in metallic Al to +3 in [Al(OH)4]−. The oxidation state of hydrogen changes from +1 in H2O to 0 in H2. Aluminum is oxidized, while hydrogen is reduced:
\( \overset{0}{Al} (s) + \overset{+1}{H}_2 O(aq) \rightarrow [ \overset{+3}{Al} (OH)_4 ]^- (aq) + \overset{0}{H_2} (g) \)
-
\( \begin{align}
& Reduction\textrm : \: Al^0 \rightarrow Al^{3+} + 3e^- \\
& Oxidation\textrm : \: H^+ + e^- \rightarrow H^0 \: (in\: H_2 )
\end{align}\) -
Multiply the reduction equation by 3 to obtain an equation with the same number of electrons as the oxidation equation:
\(\begin{align} & Reduction \textrm : \: 3H^+ + 3e^- \rightarrow 3H^0\: (in\: H_2) \\
& Oxidation \textrm : \: Al^0 \rightarrow Al^{3+} + 3e^- \end{align}\) -
Insert the actual chemical forms of the reactants and products, adjusting the coefficients as necessary to obtain the correct numbers of atoms as in step 4. Because a molecule of H2O contains two protons, in this case, 3H+ corresponds to 3/2H2O. Similarly, each molecule of hydrogen gas contains two H atoms, so 3H corresponds to 3/2H2.
\( \begin{align}
& Reduction\textrm : \: \dfrac{3}{2} H_2 O + 3e^- \rightarrow \dfrac{3}{2} H_2 \\
& Oxidation \textrm : \: Al \rightarrow [ Al ( OH )_4 ]^- + 3e^-
\end{align}\)
-
Adding the equations and canceling the electrons gives
\( Al + \dfrac{3}{2} H_2 O + \cancel{3e^-} \rightarrow [Al(OH)_4 ]^- + \dfrac{3}{2} H_2 + \cancel{3e^-} \)
\( Al + \dfrac{3}{2} H_2 O \rightarrow [Al(OH)_4 ]^- + \dfrac{3}{2} H_2 \) To remove the fractional coefficients, multiply both sides of the equation by 2:
\( 2Al + 3H_2O \rightarrow 2[Al(OH)_4]^- + 3H_2 \) -
The right side of the equation has a total charge of −2, whereas the left side has a total charge of 0. Because the reaction is carried out in basic solution, we can balance the charge by adding two OH− ions to the left side:
\(2Al + 2OH^- + 3H_2O \rightarrow 2[Al(OH)_4]^- + 3H_2 \) -
The left side of the equation contains five O atoms, and the right side contains eight O atoms. We can balance the O atoms by adding three H2O molecules to the left side:
\(2Al + 2OH^- + 6H_2O \rightarrow 2[Al(OH)_4]^- + 3H_2 \) -
Be sure the equation is balanced:
\(\begin{align} & Atoms \textrm : \: 2Al + 8O + 14H = 2Al + 8O + 14H \\
& Total\: charge \textrm : \: (2)(0) + (2)(-1) + (6)(0) = (2)(-1) + (3)(0) \end{align}\)
\(-2 = -2\) -
The balanced chemical equation is therefore
\( 2Al(s) + 2OH^-(aq) + 6H_2O(l) \rightarrow 2[Al(OH)_4]^-(aq) + 3H_2(g) \) Thus 3 mol of H2 gas are produced for every 2 mol of Al.
Exercise
The permanganate ion reacts with nitrite ion in basic solution to produce manganese(IV) oxide and nitrate ion. Write a balanced chemical equation for the reaction.
Answer: \(2MnO_4^-(aq) + 3NO_2^-(aq) + H_2O(l) \rightarrow 2MnO_2(s) + 3NO_3^-(aq) + 2OH^-(aq)\)
As suggested in Example 17 and Example 18, a wide variety of redox reactions are possible in aqueous solutions. The identity of the products obtained from a given set of reactants often depends on both the ratio of oxidant to reductant and whether the reaction is carried out in acidic or basic solution, which is one reason it can be difficult to predict the outcome of a reaction. Because oxidation–reduction reactions in solution are so common and so important, however, chemists have developed two general guidelines for predicting whether a redox reaction will occur and the identity of the products:
- Compounds of elements in high oxidation states (such as ClO4−, NO3−, MnO4−, Cr2O72−, and UF6) tend to act as oxidants and become reduced in chemical reactions.
- Compounds of elements in low oxidation states (such as CH4, NH3, H2S, and HI) tend to act as reductants and become oxidized in chemical reactions.
| Note the Pattern |
| Species in high oxidation states act as oxidants, whereas species in low oxidation states act as reductants. |
When an aqueous solution of a compound that contains an element in a high oxidation state is mixed with an aqueous solution of a compound that contains an element in a low oxidation state, an oxidation–reduction reaction is likely to occur.


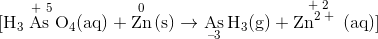.gif?revision=3&size=bestfit&width=350&height=36)

