2.7: The Concept of Mole and the Avogadro Constant
- Page ID
- 24179
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\[ 2 \times \text { atomic mass of carbon} = 2 \, atoms \left ( {12.011 \, amu \over atoms } \right ) = 24.022 \,amu \]
\[ 6 \times \text { atomic mass of hydrogen} = 2 \, atoms \left ( {1.0079 \, amu \over atoms } \right ) = 6.0474 \,amu \]
\[ 1 \times \text { atomic mass of oxygen} = 1 \, atoms \left ( {15.9994 \, amu \over atoms } \right ) = 15.994 \,amu \]
C Adding together the masses gives the molecular mass:
\[ 24.022 \,amu + 6.0474 \,amu + 15.9994 \,amu = 46.069 \,amu\]
Alternatively, we could have used unit conversions to reach the result in one step:
\[ \left [ 2 \, atoms C \left ( {12.011 \, amu \over 1 \, atom C} \right ) \right ] + \left [ 6 \, atoms H \left ( {1.0079 \, amu \over 1 \, atom H} \right ) \right ] + \left [ 1 \, atoms C \left ( {15.9994 \, amu \over 1 \, atom 0} \right ) \right ] = 46.069 \, amu \]
The same calculation can also be done in a tabular format, which is especially helpful for more complex molecules:
\[ 2 C \, \, \, (2\, atoms) (12.011 \, amu/atom ) = 24.022 \, amu \]
\[ 6 H \, \, \, (6\, atoms) (1.0079 \, amu/atom ) = 6.0474 \, amu \]
\[ + 1O \, \, \, (1\, atoms) (15.9994 \, amu/atom ) = 15.9994 \, amu \]
\[ C_2H_6O \, \, \, \, \, \text {molecular mass of ethanol} = 46.069 \, amu \]
Calculate the molecular mass of trichlorofluoromethane, also known as Freon-11, whose condensed structural formula is \(CCl_3F\). Until recently, it was used as a refrigerant. The structure of a molecule of Freon-11 is as follows:
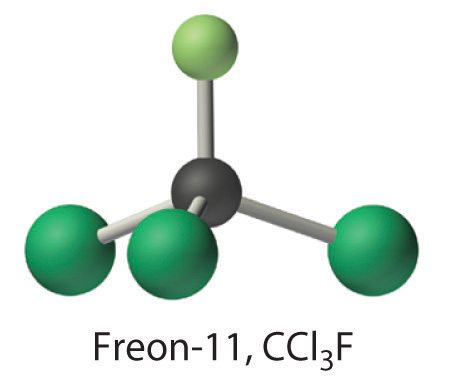
Answer: 137.368 \,amu
Unlike molecules, which form covalent bonds, ionic compounds do not have a readily identifiable molecular unit. Therefore, for ionic compounds, the formula mass (also called the empirical formula mass) of the compound is used instead of the molecular mass. The formula mass is the sum of the atomic masses of all the elements in the empirical formula, each multiplied by its subscript (written or implied). It is directly analogous to the molecular mass of a covalent compound. The units are atomic mass units.
Atomic mass, molecular mass, and formula mass all have the same units: atomic mass units.
Determining the Molar Mass of a Molecule: https://youtu.be/wOjQjZqX7l8
Calculate the formula mass of Ca3(PO4)2, commonly called calcium phosphate. This compound is the principal source of calcium found in bovine milk.
Given: ionic compound
Asked for: formula mass
Strategy:
- Determine the number of atoms of each element in the empirical formula.
- Obtain the atomic masses of each element from the periodic table and multiply the atomic mass of each element by the number of atoms of that element.
- Add together the masses to give the formula mass.
Solution:
A The empirical formula—Ca3(PO4)2—indicates that the simplest electrically neutral unit of calcium phosphate contains three Ca2+ ions and two PO43− ions. The formula mass of this molecular unit is calculated by adding together the atomic masses of three calcium atoms, two phosphorus atoms, and eight oxygen atoms.
B Taking atomic masses from the periodic table, we obtain
\[ 3 \times \text {atomic mass of calcium} = 3 \, atoms \left ( {40.078 \, amu \over atom } \right ) = 120.234 \, amu \]
\[ 2 \times \text {atomic mass of phosphorus} = 2 \, atoms \left ( {30.973761 \, amu \over atom } \right ) = 61.947522 \, amu \]
\[ 8 \times \text {atomic mass of oxygen} = 8 \, atoms \left ( {15.9994 \, amu \over atom } \right ) = 127.9952 \, amu \]
C Adding together the masses gives the formula mass of Ca3(PO4)2:
\[120.234 \,amu + 61.947522 \, amu + 127.9952 \, amu = 310.177 \, amu \]
We could also find the formula mass of Ca3(PO4)2 in one step by using unit conversions or a tabular format:
\[ \left [ 3 \, atoms Ca \left ({40.078 \, amu \over 1 \, atom Ca } \right ) \right ] + \left [ 2 \, atoms P \left ({30.973761 \, amu \over 1 \, atom P } \right ) \right ] + \left [ 8 \, atoms O \left ({15.9994 \, amu \over 1 \, atom O } \right ) \right ] \]
\[= 310.177 \,amu \]
\[ 2P \, \, \, \, (2\, atoms)(30.973761 \, amu/atom) = 61.947522 \, amu \]
\[ + 8O \, \, \, \, (8\, atoms)(15.9994 \, amu/atom) = 127.9952 \, amu \]
\[ Ca_3P_2O_8 \, \, \, \, \text {formula mass of Ca}_3(PO_4)_2 = 310.177 \, amu \]
\[(moles)(molar mass) \rightarrow mass \label{2.7.1}\]
or, more specifically,
\[ moles \left ( {grams \over mole } \right ) = grams \]
Conversely, to convert the mass of a substance to moles:
\[ \left ( { grams \over grams/mole} \right ) = grams \left ( {mole \over grams } \right ) = moles \label{2.7.2B}\]
\[2H_{2(g)} + O_{2(g)} \rightarrow 2H_2O_{(l)}\]
the production of two moles of water would require the consumption of 2 moles of \(H_2\) and one mole of \(O_2\). Therefore, when considering this particular reaction
- 2 moles of H2
- 1 mole of O2 and
- 2 moles of H2O
would be considered to be stoichiometrically equivalent quantitites.
These stoichiometric relationships, derived from balanced equations, can be used to determine expected amounts of products given amounts of reactants. For example, how many moles of \(H_2O\) would be produced from 1.57 moles of \(O_2\)?
\[ (1.57\; mol\; O_2) \left( \dfrac{2\; mol H_2O}{1\;mol\;O_2} \right) = 3.14\; mol\; H_2O\]
The ratio \( \left( \dfrac{2\; mol\; H_2O}{1\;mol\;O_2} \right)\) is the stoichiometric relationship between \(H_2O\) and \(O_2\) from the balanced equation for this reaction.
For the combustion of butane (\(C_4H_{10}\)) the balanced equation is:
\[2C_4H_{10(l)} + 13O_{2(g)} \rightarrow 8CO_{2(g)} + 10H_2O_{(l)}\]
Calculate the mass of \(CO_2\) that is produced in burning 1.00 gram of \(C_4H_{10}\).
Solution
Thus, the overall sequence of steps to solve this problem is:
First of all we need to calculate how many moles of butane we have in a 1.00 gram sample:
\[ (1.00\; g\; C_4H_{10}) \left(\dfrac{1\; mol\; C_4H_{10}}{58.0\;g\; C_4H_{10}}\right) = 1.72 \times 10^{-2} \; mol\; C_4H_{10}\]
Now, the stoichiometric relationship between \(C_4H_{10}\) and \(CO_2\) is:
\[\left( \dfrac{8\; mol\; CO_2}{2\; mol\; C_4H_{10}}\right)\]
Therefore:
\[ \left(\dfrac{8\; mol\; CO_2}{2\; mol\; C_4H_{10}} \right) \times 1.72 \times 10^{-2} \; mol\; C_4H_{10} = 6.88 \times 10^{-2} \; mol\; CO_2\]
The question called for the determination of the mass of \(CO_2\) produced, thus we have to convert moles of \(CO_2\) into grams (by using the molecular weight of \(CO_2\)):
\[ 6.88 \times 10^{-2} \; mol\; CO_2 \left( \dfrac{44.0\; g\; CO_2}{1\; mol\; CO_2} \right) = 3.03\;g \; CO_2\]
Be sure to pay attention to the units when converting between mass and moles. Figure \(\PageIndex{1}\) is a flowchart for converting between mass; the number of moles; and the number of atoms, molecules, or formula units. The use of these conversions is illustrated in Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).

Conversions Between Grams, Mol, & Atoms: https://youtu.be/rOvErpAnoCg
For 35.00 g of ethylene glycol (HOCH2CH2OH), which is used in inks for ballpoint pens, calculate the number of
- moles.
- molecules.
Given: mass and molecular formula
Asked for: number of moles and number of molecules
Strategy:
- Use the molecular formula of the compound to calculate its molecular mass in grams per mole.
- Convert from mass to moles by dividing the mass given by the compound’s molar mass.
- Convert from moles to molecules by multiplying the number of moles by Avogadro’s number.
Solution:
a. A The molecular mass of ethylene glycol can be calculated from its molecular formula using the method illustrated in Example \(\PageIndex{2}\).7.1:
\[ 2C (2 \,atoms )(12.011 \, amu/atom) = 24.022 \, amu \]
\[ 6H (6 \,atoms )(1.0079 \, amu/atom) = 6.0474 \, amu \]
\[ 2O (2 \,atoms )(15.9994 \, amu/atom) = 31.9988 \, amu \]
The molar mass of ethylene glycol is 62.068 g/mol.
B The number of moles of ethylene glycol present in 35.00 g can be calculated by dividing the mass (in grams) by the molar mass (in grams per mole):
\[ { \text {mass of ethylene glycol (g)} \over \text {molar mass (g/mol)} } = \text {moles ethylene glycol (mol) }\]
So
\[ 35.00 \, g \text {ethylene glycol} \left ( {1 \, mole \text {ethylene glycol} \over 62.068 \, g \text {ethylene glycol } } \right ) = 0.5639 \,mol \text {ethylene glycol} \]
It is always a good idea to estimate the answer before you do the actual calculation. In this case, the mass given (35.00 g) is less than the molar mass, so the answer should be less than 1 mol. The calculated answer (0.5639 mol) is indeed less than 1 mol, so we have probably not made a major error in the calculations.
b. C To calculate the number of molecules in the sample, we multiply the number of moles by Avogadro’s number:
\[ \text {molecules of ethylene glycol} = 0.5639 \, mol \left ( {6.022 \times 10^{23} \, molecules \over 1 \, mol } \right ) \]
\[ = 3.396 \times 10^{23} \, molecules \]
Because we are dealing with slightly more than 0.5 mol of ethylene glycol, we expect the number of molecules present to be slightly more than one-half of Avogadro’s number, or slightly more than 3 × 1023 molecules, which is indeed the case.
\[ 2S (2 \, atoms)(32.065 \, amu/atom ) = 64.130 \, amu \]
\[+ 2Cl (2 \, atoms )(35.453 \, amu/atom ) = 70.906 \, amu \]
\[ S_2 Cl_2 \text {molecular mass of } S_2Cl_2 = 135.036 \, amu \]
The molar mass of S2Cl2 is 135.036 g/mol.
B The mass of 1.75 mol of S2Cl2 is calculated as follows:
\[moles S_2Cl_2 \left [\text {molar mass}\left ({ g \over mol} \right )\right ] \rightarrow mass of S_2Cl_2 \, (g) \]
\[ 1.75 \, mol S_2Cl_2\left ({135.036 \, g S_2Cl_2 \over 1 \, mol S_2Cl_2 } \right ) = 236 \, g S_2Cl_2 \]
b.
A The formula mass of Ca(ClO)2 is obtained as follows:
\[1Ca (1 \, atom)(40.078 \, amu/atom) = 40.078 \, amu \]
\[2Cl (2 \, atoms)(35.453 \, amu/atom) = 70.906 \, amu \]
\[+ 2O (2 \, atoms)(15.9994 \, amu/atom) = 31.9988 \, amu \]
\[ Ca (ClO)_2 \text { formula mass of } Ca (ClO)_2 = 142.983 \, amu\]
The molar mass of Ca(ClO)2 142.983 g/mol.
B The mass of 1.75 mol of Ca(ClO)2 is calculated as follows:
\[ 1.75 \, mol Ca(ClO)_2 \left [ {142.983 \, g Ca(ClO)_2 \over 1 \, mol Ca(ClO)_2 } \right ] = 250 \, g Ca(ClO)_2 \]
Because 1.75 mol is less than 2 mol, the final quantity in grams in both cases should be less than twice the molar mass, which it is.
Calculate the mass of 0.0122 mol of each compound.
- Si3N4 (silicon nitride), used as bearings and rollers
- (CH3)3N (trimethylamine), a corrosion inhibitor
Answer:
- 1.71 g
- 0.721 g
The coefficients in a balanced chemical equation can be interpreted both as the relative numbers of molecules involved in the reaction and as the relative number of moles. For example, in the balanced equation:
\[2H_{2(g)} + O_{2(g)} \rightarrow 2H_2O_{(l)}\]
the production of two moles of water would require the consumption of 2 moles of \(H_2\) and one mole of \(O_2\). Therefore, when considering this particular reaction
- 2 moles of H2
- 1 mole of O2 and
- 2 moles of H2O
would be considered to be stoichiometrically equivalent quantitites.
These stoichiometric relationships, derived from balanced equations, can be used to determine expected amounts of products given amounts of reactants. For example, how many moles of \(H_2O\) would be produced from 1.57 moles of \(O_2\)?
\[ (1.57\; mol\; O_2) \left( \dfrac{2\; mol H_2O}{1\;mol\;O_2} \right) = 3.14\; mol\; H_2O\]
The ratio \( \left( \dfrac{2\; mol\l H_2O}{1\;mol\;O_2} \right)\) is the stoichiometric relationship between \(H_2O\) and \(O_2\) from the balanced equation for this reaction.
For the combustion of butane (\(C_4H_{10}\)) the balanced equation is:
\[2C_4H_{10(l)} + 13O_{2(g)} \rightarrow 8CO_{2(g)} + 10H_2O_{(l)}\]
Calculate the mass of \(CO_2\) that is produced in burning 1.00 gram of \(C_4H_{10}\).
Solution
First of all we need to calculate how many moles of butane we have in a 1.00 gram sample:
\[ (1.00\; g\; C_4H_{10}) \left(\dfrac{1\; mol\; C_4H_{10}}{58.0\;g\; C_4H_{10}}\right) = 1.72 \times 10^{-2} \; mol\; C_4H_{10}\]
Now, the stoichiometric relationship between \(C_4H_{10}\) and \(CO_2\) is:
\[\left( \dfrac{8\; mol\; CO_2}{2\; mol\; C_4H_{10}}\right)\]
Therefore:
\[ \left(\dfrac{8\; mol\; CO_2}{2\; mol\; C_4H_{10}} \right) \times 1.72 \times 10^{-2} \; mol\; C_4H_{10} = 6.88 \times 10^{-2} \; mol\; CO_2\]
The question called for the determination of the mass of \(CO_2\) produced, thus we have to convert moles of \(CO_2\) into grams (by using the molecular weight of \(CO_2\)):
\[ 6.88 \times 10^{-2} \; mol\; CO_2 \left( \dfrac{44.0\; g\; CO_2}{1\; mol\; CO_2} \right) = 3.03\;g \; CO_2\]
Thus, the overall sequence of steps to solve this problem were:
In a similar way we could determine the mass of water produced, or oxygen consumed, etc.
Summary
- To analyze chemical transformations, it is essential to use a standardized unit of measure called the mole.
The molecular mass and the formula mass of a compound are obtained by adding together the atomic masses of the atoms present in the molecular formula or empirical formula, respectively; the units of both are atomic mass units (amu). The mole is a unit used to measure the number of atoms, molecules, or (in the case of ionic compounds) formula units in a given mass of a substance. The mole is defined as the amount of substance that contains the number of carbon atoms in exactly 12 g of carbon-12, Avogadro’s number (6.022 × 1023) of atoms of carbon-12. The molar mass of a substance is defined as the mass of 1 mol of that substance, expressed in grams per mole, and is equal to the mass of 6.022 × 1023 atoms, molecules, or formula units of that substance.

