9.4: Covalent Bonding and Orbital Overlap
- Page ID
- 21754
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- To describe the bonding in simple compounds using valence bond theory.
Although the VSEPR model is a simple and useful method for qualitatively predicting the structures of a wide range of compounds, it is not infallible. It predicts, for example, that H2S and PH3 should have structures similar to those of \(\ce{H2O}\) and \(\ce{NH3}\), respectively. In fact, structural studies have shown that the H–S–H and H–P–H angles are more than 12° smaller than the corresponding bond angles in \(\ce{H2O}\) and \(\ce{NH3}\). More disturbing, the VSEPR model predicts that the simple group 2 halides (MX2), which have four valence electrons, should all have linear X–M–X geometries. Instead, many of these species, including \(\ce{SrF2}\) and \(\ce{BaF2}\), are significantly bent. A more sophisticated treatment of bonding is needed for systems such as these. In this section, we present a quantum mechanical description of bonding, in which bonding electrons are viewed as being localized between the nuclei of the bonded atoms. The overlap of bonding orbitals is substantially increased through a process called hybridization, which results in the formation of stronger bonds.
Introduction
As we have talked about using Lewis structures to depict the bonding in covalent compounds, we have been very vague in our language about the actual nature of the chemical bonds themselves. We know that a covalent bond involves the ‘sharing’ of a pair of electrons between two atoms - but how does this happen, and how does it lead to the formation of a bond holding the two atoms together?
The valence bond theory is introduced to describe bonding in covalent molecules. In this model, bonds are considered to form from the overlapping of two atomic orbitals on different atoms, each orbital containing a single electron. In looking at simple inorganic molecules such as H2 or HF, our present understanding of s and p atomic orbitals will suffice. To explain the bonding in organic molecules, however, we will need to introduce the concept of hybrid orbitals.
Example: The H2 molecule
The simplest case to consider is the hydrogen molecule, H2. When we say that the two electrons from each of the hydrogen atoms are shared to form a covalent bond between the two atoms, what we mean in valence bond theory terms is that the two spherical 1s orbitals overlap, allowing the two electrons to form a pair within the two overlapping orbitals. In simple terms, we can say that both electrons now spend more time between the two nuclei and thus hold the atoms together. As we will see, the situation is not quite so simple as that, because the electron pair must still obey quantum mechanics - that is, the two electrons must now occupy a shared orbital space. This will be the essential principle of valence bond theory.

How far apart are the two nuclei? That is a very important issue to consider. If they are too far apart, their respective 1s orbitals cannot overlap, and thus no covalent bond can form - they are still just two separate hydrogen atoms. As they move closer and closer together, orbital overlap begins to occur, and a bond begins to form. This lowers the potential energy of the system, as new, attractive positive-negative electrostatic interactions become possible between the nucleus of one atom and the electron of the second. However, something else is happening at the same time: as the atoms get closer, the repulsive positive-positive interaction between the two nuclei also begins to increase.
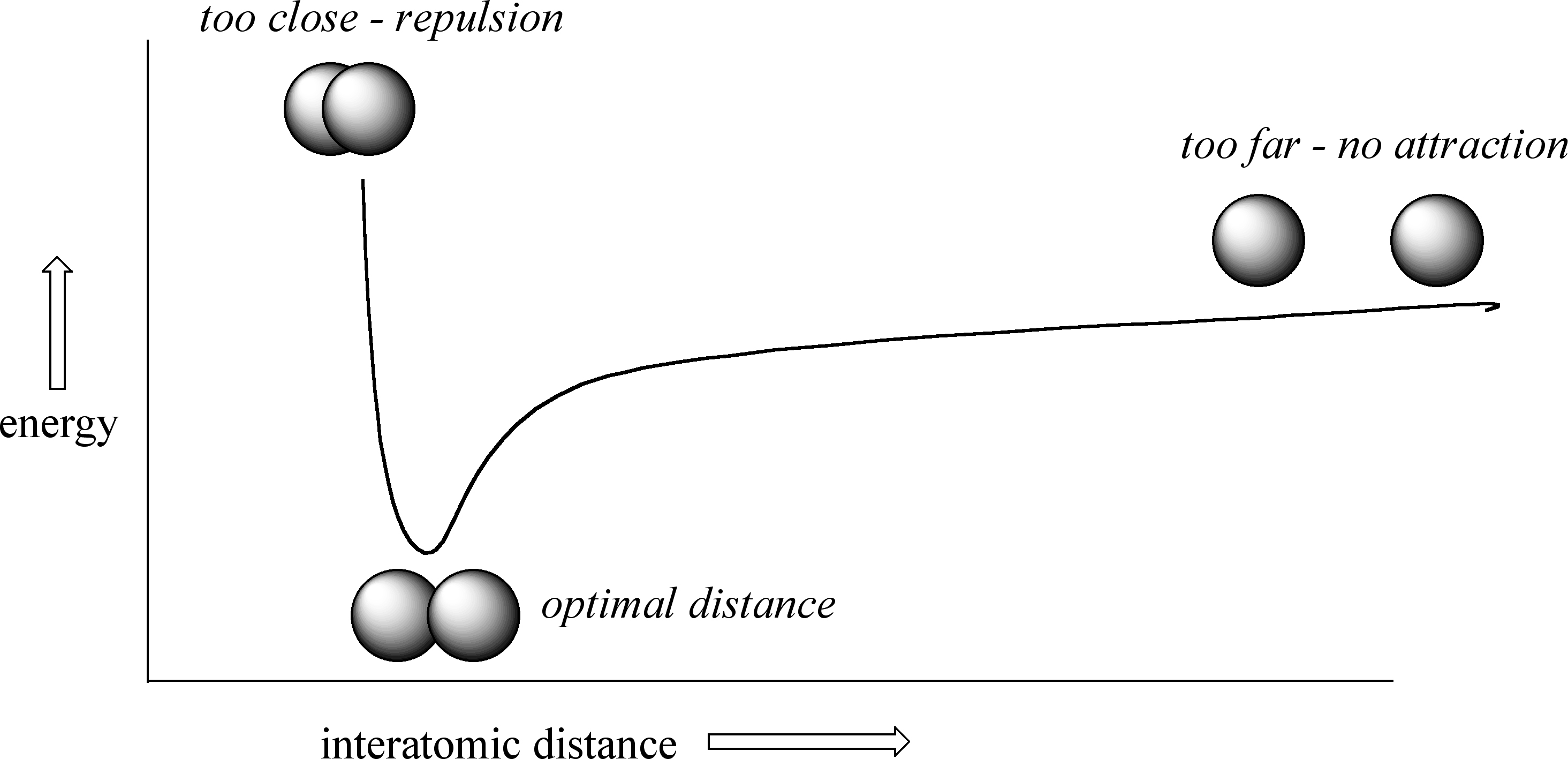
At first this repulsion is more than offset by the attraction between nuclei and electrons, but at a certain point, as the nuclei get even closer, the repulsive forces begin to overcome the attractive forces, and the potential energy of the system rises quickly. When the two nuclei are ‘too close’, we have a very unstable, high-energy situation. There is a defined optimal distance between the nuclei in which the potential energy is at a minimum, meaning that the combined attractive and repulsive forces add up to the greatest overall attractive force. This optimal internuclear distance is the bond length. For the H2 molecule, this distance is 74 x 10-12 meters, or 0.74 Å (Å means angstrom, or 10-10 meters). Likewise, the difference in potential energy between the lowest state (at the optimal internuclear distance) and the state where the two atoms are completely separated is called the bond energy. For the hydrogen molecule, this energy is equal to about 104 kcal/mol.
Every covalent bond in a given molecule has a characteristic length and strength. In general, carbon-carbon single bonds are about 1.5 Å long (Å means angstrom, or 10-10 meters) while carbon-carbon double bonds are about 1.3 Å, carbon-oxygen double bonds are about 1.2 Å, and carbon-hydrogen bonds are in the range of 1.0 – 1.1 Å. Most covalent bonds in organic molecules range in strength from just under 100 kcal/mole (for a carbon-hydrogen bond in ethane, for example) up to nearly 200 kcal/mole. You can refer to tables in reference books such as the CRC Handbook of Chemistry and Physics for extensive lists of bond lengths, strengths, and many other data for specific organic compounds.
Although we tend to talk about "bond length" as a specific distance, it is not accurate to picture covalent bonds as rigid sticks of unchanging length - rather, it is better to picture them as springs which have a defined length when relaxed, but which can be compressed, extended, and bent. This ‘springy’ picture of covalent bonds will become very important, when we study the analytical technique known as infrared (IR) spectroscopy.
Valence Bond Theory: A Localized Bonding Approach
You learned that as two hydrogen atoms approach each other from an infinite distance, the energy of the system reaches a minimum. This region of minimum energy in the energy diagram corresponds to the formation of a covalent bond between the two atoms at an H–H distance of 74 pm (Figure \(\PageIndex{1}\)). According to quantum mechanics, bonds form between atoms because their atomic orbitals overlap, with each region of overlap accommodating a maximum of two electrons with opposite spin, in accordance with the Pauli principle. In this case, a bond forms between the two hydrogen atoms when the singly occupied 1s atomic orbital of one hydrogen atom overlaps with the singly occupied 1s atomic orbital of a second hydrogen atom. Electron density between the nuclei is increased because of this orbital overlap and results in a localized electron-pair bond (Figure \(\PageIndex{1}\)).
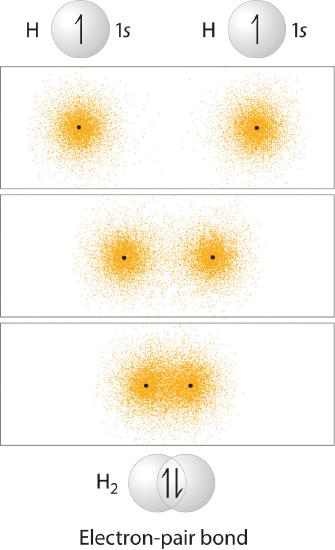
Although Lewis and VSEPR structures also contain localized electron-pair bonds, neither description uses an atomic orbital approach to predict the stability of the bond. Doing so forms the basis for a description of chemical bonding known as valence bond theory, which is built on two assumptions:
- The strength of a covalent bond is proportional to the amount of overlap between atomic orbitals; that is, the greater the overlap, the more stable the bond.
- An atom can use different combinations of atomic orbitals to maximize the overlap of orbitals used by bonded atoms.
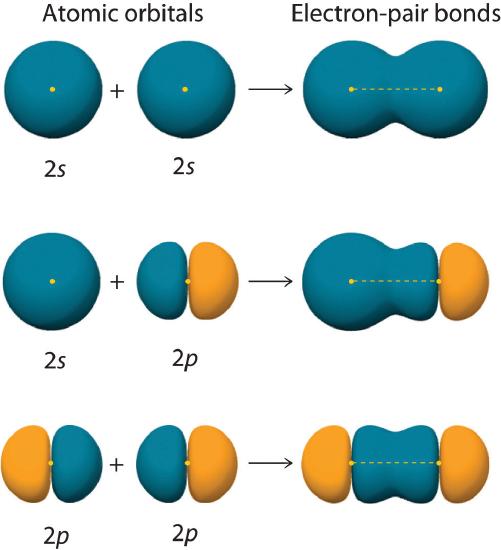
Figure \(\PageIndex{2}\) shows an electron-pair bond formed by the overlap of two ns atomic orbitals, two np atomic orbitals, and an ns and an np orbital where n = 2. Notice that bonding overlap occurs when the interacting atomic orbitals have the correct orientation (are "pointing at" each other) and are in phase (represented by colors in Figure \(\PageIndex{2}\) ).
Maximum overlap occurs between orbitals with the same spatial orientation and similar energies.
Let’s examine the bonds in BeH2, for example. According to the VSEPR model, BeH2 is a linear compound with four valence electrons and two Be–H bonds. Its bonding can also be described using an atomic orbital approach. Beryllium has a 1s22s2 electron configuration, and each H atom has a 1s1 electron configuration. Because the Be atom has a filled 2s subshell, however, it has no singly occupied orbitals available to overlap with the singly occupied 1s orbitals on the H atoms. If a singly occupied 1s orbital on hydrogen were to overlap with a filled 2s orbital on beryllium, the resulting bonding orbital would contain three electrons, but the maximum allowed by quantum mechanics is two. How then is beryllium able to bond to two hydrogen atoms? One way would be to add enough energy to excite one of its 2s electrons into an empty 2p orbital and reverse its spin, in a process called promotion:

In this excited state, the Be atom would have two singly occupied atomic orbitals (the 2s and one of the 2p orbitals), each of which could overlap with a singly occupied 1s orbital of an H atom to form an electron-pair bond. Although this would produce \(\ce{BeH2}\), the two Be–H bonds would not be equivalent: the 1s orbital of one hydrogen atom would overlap with a Be 2s orbital, and the 1s orbital of the other hydrogen atom would overlap with an orbital of a different energy, a Be 2p orbital. Experimental evidence indicates, however, that the two Be–H bonds have identical energies. To resolve this discrepancy and explain how molecules such as \(\ce{BeH2}\) form, scientists developed the concept of hybridization.
Contributors and Attributions
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

