6.2: Quantized Energy and Photons
- Page ID
- 21729
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)↵
- To understand how energy is quantized.
By the late 19th century, many physicists thought their discipline was well on the way to explaining most natural phenomena. They could calculate the motions of material objects using Newton’s laws of classical mechanics, and they could describe the properties of radiant energy using mathematical relationships known as Maxwell’s equations, developed in 1873 by James Clerk Maxwell, a Scottish physicist. The universe appeared to be a simple and orderly place, containing matter, which consisted of particles that had mass and whose location and motion could be accurately described, and electromagnetic radiation, which was viewed as having no mass and whose exact position in space could not be fixed. Thus matter and energy were considered distinct and unrelated phenomena. Soon, however, scientists began to look more closely at a few inconvenient phenomena that could not be explained by the theories available at the time.
Blackbody Radiation
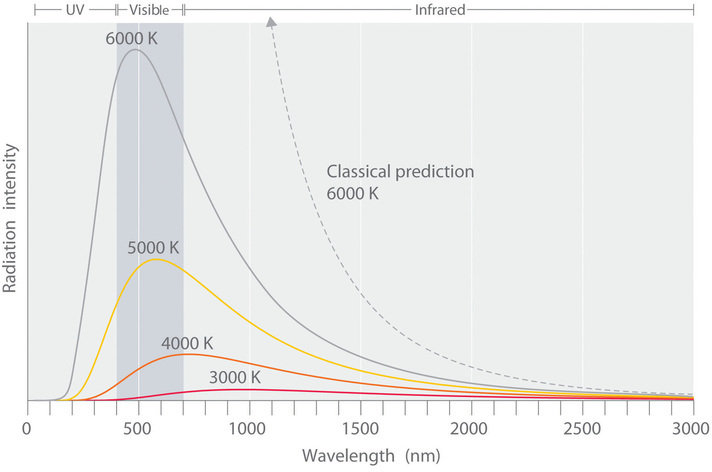
One phenomenon that seemed to contradict the theories of classical physics was blackbody radiation, which is electromagnetic radiation given off by a hot object. The wavelength (i.e. color) of radiant energy emitted by a blackbody depends on only its temperature, not its surface or composition. Hence an electric stove burner or the filament of a space heater glows dull red or orange when heated, whereas the much hotter tungsten wire in an incandescent light bulb gives off a yellowish light.


The intensity of radiation is a measure of the energy emitted per unit area. A plot of the intensity of blackbody radiation as a function of wavelength for an object at various temperatures is shown in Figure \(\PageIndex{2}\). One of the major assumptions of classical physics was that energy increased or decreased in a smooth, continuous manner. For example, classical physics predicted that as wavelength decreased, the intensity of the radiation an object emits should increase in a smooth curve without limit at all temperatures, as shown by the broken line for 6000 K in Figure \(\PageIndex{2}\). Thus classical physics could not explain the sharp decrease in the intensity of radiation emitted at shorter wavelengths (primarily in the ultraviolet region of the spectrum), which was referred to as the “ultraviolet catastrophe.” In 1900, however, the German physicist Max Planck (1858–1947) explained the ultraviolet catastrophe by proposing (in what he called "an act of despair") that the energy of electromagnetic waves is quantized rather than continuous. This means that for each temperature, there is a maximum intensity of radiation that is emitted in a blackbody object, corresponding to the peaks in Figure \(\PageIndex{2}\), so the intensity does not follow a smooth curve as the temperature increases, as predicted by classical physics. Thus energy could be gained or lost only in integral multiples of some smallest unit of energy, a quantum.
In addition to being a physicist, Planck was a gifted pianist, who at one time considered music as a career. During the 1930s, Planck felt it was his duty to remain in Germany, despite his open opposition to the policies of the Nazi government.

One of his sons was executed in 1944 for his part in an unsuccessful attempt to assassinate Hitler, and bombing during the last weeks of World War II destroyed Planck’s home. After WWII, the major German scientific research organization was renamed the Max Planck Society.
Although quantization may seem to be an unfamiliar concept, we encounter it frequently. For example, US money is integral multiples of pennies. Similarly, musical instruments like a piano or a trumpet can produce only certain musical notes, such as C or F sharp. Because these instruments cannot produce a continuous range of frequencies, their frequencies are quantized. Even electrical charge is quantized: an ion may have a charge of −1 or −2 but not −1.33 electron charges.
Planck postulated that the energy of a particular quantum of radiant energy could be described by the equation
\[ E=h u \label{6.2.1} \]
where the proportionality constant h is called Planck’s constant, one of the most accurately known fundamental constants in science. For our purposes, its value to four significant figures is generally sufficient:
\[h = 6.626 \times 10^{−34}\, J•s\, (\text{joule-segundos}) \nonumber \]
As the frequency of electromagnetic radiation increases, the magnitude of the associated quantum of radiant energy increases. By assuming that energy can be emitted by an object only in integral multiples of hν, Planck devised an equation that fit the experimental data shown in Figure \(\PageIndex{2}\). We can understand Planck’s explanation of the ultraviolet catastrophe qualitatively as follows: At low temperatures, radiation with only relatively low frequencies is emitted, corresponding to low-energy quanta. As the temperature of an object increases, there is an increased probability of emitting radiation with higher frequencies, corresponding to higher-energy quanta. At any temperature, however, it is simply more probable for an object to lose energy by emitting a large number of lower-energy quanta than a single very high-energy quantum that corresponds to ultraviolet radiation. The result is a maximum in the plot of intensity of emitted radiation versus wavelength, as shown in Figure \(\PageIndex{2}\), and a shift in the position of the maximum to lower wavelength (higher frequency) with increasing temperature.
At the time he proposed his radical hypothesis, Planck could not explain why energies should be quantized. Initially, his hypothesis explained only one set of experimental data—blackbody radiation. If quantization were observed for a large number of different phenomena, then quantization would become a law. In time, a theory might be developed to explain that law. As things turned out, Planck’s hypothesis was the seed from which modern physics grew.
Energy of a Photon: Energy of a Photon, YouTube(opens in new window) [youtu.be]
The Photoelectric Effect
Only five years after he proposed it, Planck’s quantization hypothesis was used to explain a second phenomenon that conflicted with the accepted laws of classical physics. When certain metals are exposed to light, electrons are ejected from their surface (Figure \(\PageIndex{3}\)). Classical physics predicted that the number of electrons emitted and their kinetic energy should depend on only the intensity of the light, not its frequency. In fact, however, each metal was found to have a characteristic threshold frequency of light; below that frequency, no electrons are emitted regardless of the light’s intensity. Above the threshold frequency, the number of electrons emitted was found to be proportional to the intensity of the light, and their kinetic energy was proportional to the frequency. This phenomenon was called the photoelectric effect (A phenomenon in which electrons are ejected from the surface of a metal that has been exposed to light).
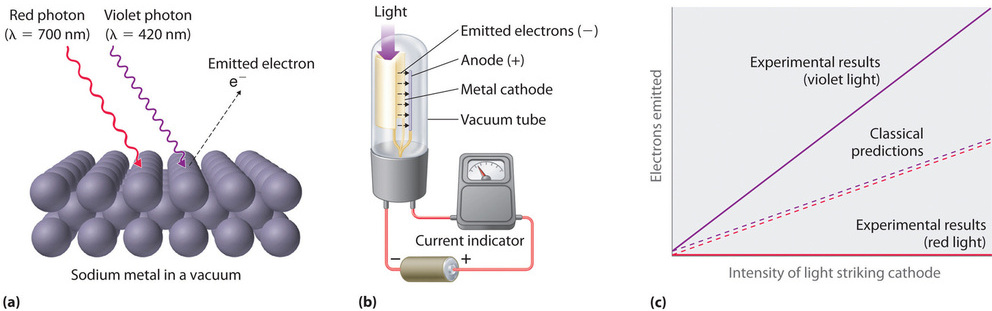
Albert Einstein (1879–1955; Nobel Prize in Physics, 1921) quickly realized that Planck’s hypothesis about the quantization of radiant energy could also explain the photoelectric effect. The key feature of Einstein’s hypothesis was the assumption that radiant energy arrives at the metal surface in particles that we now call photons (a quantum of radiant energy, each of which possesses a particular energy energy \(E\) given by Equation \(\ref{6.2.1}\) Einstein postulated that each metal has a particular electrostatic attraction for its electrons that must be overcome before an electron can be emitted from its surface (\(E_o= u_o\)). If photons of light with energy less than Eo strike a metal surface, no single photon has enough energy to eject an electron, so no electrons are emitted regardless of the intensity of the light. If a photon with energy greater than Eo strikes the metal, then part of its energy is used to overcome the forces that hold the electron to the metal surface, and the excess energy appears as the kinetic energy of the ejected electron:
\[ \begin{align} \text{ kinetic energy of ejected electron} &=E-E_{o} \nonumber \\[4pt] &=h u -h u _{o} \nonumber \\[4pt] &=h\left ( u - u _{o} \right ) \label{6.2.2} \end{align} \]
When a metal is struck by light with energy above the threshold energy Eo, the number of emitted electrons is proportional to the intensity of the light beam, which corresponds to the number of photons per square centimeter, but the kinetic energy of the emitted electrons is proportional to the frequency of the light. Thus Einstein showed that the energy of the emitted electrons depended on the frequency of the light, contrary to the prediction of classical physics. Moreover, the idea that light could behave not only as a wave but as a particle in the form of photons suggested that matter and energy might not be such unrelated phenomena after all.
The Photoelectric Effect: The Photoelectric Effect, YouTube(opens in new window) [youtu.be]

In 1900, Einstein was working in the Swiss patent office in Bern. He was born in Germany and throughout his childhood his parents and teachers had worried that he might be developmentally disabled. The patent office job was a low-level civil service position that was not very demanding, but it did allow Einstein to spend a great deal of time reading and thinking about physics.

In 1905, his "miracle year" he published four papers that revolutionized physics. One was on the special theory of relativity, a second on the equivalence of mass and energy, a third on Brownian motion, and the fourth on the photoelectric effect, for which he received the Nobel Prize in 1921, the theory of relativity and energy-matter equivalence being still controversial at the time
Planck’s and Einstein’s postulate that energy is quantized is in many ways similar to Dalton’s description of atoms. Both theories are based on the existence of simple building blocks, atoms in one case and quanta of energy in the other. The work of Planck and Einstein thus suggested a connection between the quantized nature of energy and the properties of individual atoms.
A ruby laser, a device that produces light in a narrow range of wavelengths emits red light at a wavelength of 694.3 nm (Figure \(\PageIndex{4}\)). What is the energy in joules of a single photon?
Given: wavelength
Asked for: energy of single photon.
Strategy:
Use Equation \(\ref{6.2.1}\) and the relationship between wavelength and frequency to calculate the energy in joules.
Solution:
The energy of a single photon is given by Equaton \ref{6.2.1}\[E = hu = \dfrac{hc}{λ}. \nonumber \]
An x-ray generator, such as those used in hospitals, emits radiation with a wavelength of 1.544 Å.
- What is the energy in joules of a single photon?
- How many times more energetic is a single x-ray photon of this wavelength than a photon emitted by a ruby laser?
- Answer a
-
\(1.287 \times 10^{-15}\; J/photon\)
- Answer b
-
4497 times
Summary
The fundamental building blocks of energy are quanta and of matter are atoms. The properties of blackbody radiation, the radiation emitted by hot objects, could not be explained with classical physics. Max Planck postulated that energy was quantized and could be emitted or absorbed only in integral multiples of a small unit of energy, known as a quantum. The energy of a quantum is proportional to the frequency of the radiation; the proportionality constant \(h\) is a fundamental constant (Planck’s constant). Albert Einstein used Planck’s concept of the quantization of energy to explain the photoelectric effect, the ejection of electrons from certain metals when exposed to light. Einstein postulated the existence of what today we call photons, particles of light with a particular energy, \(E = h u\). Both energy and matter have fundamental building blocks: quanta and atoms, respectively.
Contributors and Attributions
Modified by Joshua Halpern (Howard University)

