1.E: Matter and Measurement (Exercises)
- Page ID
- 24745
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)These are homework exercises to accompany the Textmap created for "Chemistry: The Central Science" by Brown et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.
1.2
CONCEPTUAL PROBLEMS
Please be sure you are familiar with the topics discussed in Essential Skills 1 (Section 1.9) before proceeding to the Conceptual Problems.
- What is the difference between mass and weight? Is the mass of an object on Earth the same as the mass of the same object on Jupiter? Why or why not?
- Is it accurate to say that a substance with a mass of 1 kg weighs 2.2 lb? Why or why not?
- What factor must be considered when reporting the weight of an object as opposed to its mass?
- Construct a table with the headings “Solid,” “Liquid,” and “Gas.” For any given substance, state what you expect for each of the following:
- the relative densities of the three phases
- the physical shapes of the three phases
- the volumes for the same mass of compound
- the sensitivity of the volume of each phase to changes in temperature
- the sensitivity of the volume to changes in pressure
- Classify each substance as homogeneous or heterogeneous and explain your reasoning.
- platinum
- a carbonated beverage
- bronze
- wood
- natural gas
- Styrofoam
- Classify each substance as homogeneous or heterogeneous and explain your reasoning.
- snowflakes
- gasoline
- black tea
- plastic wrap
- blood
- water containing ice cubes
- Classify each substance as a pure substance or a mixture and explain your reasoning.
- seawater
- coffee
- 14-karat gold
- diamond
- distilled water
- Classify each substance as a pure substance or a mixture.
- cardboard
- caffeine
- tin
- a vitamin tablet
- helium gas
- Classify each substance as an element or a compound.
- sugar
- silver
- rust
- rubbing alcohol
- copper
- Classify each substance as an element or a compound.
- water
- iron
- hydrogen gas
- glass
- nylon
- What techniques could be used to separate each of the following?
- sugar and water from an aqueous solution of sugar
- a mixture of sugar and sand
- a heterogeneous mixture of solids with different solubilities
- What techniques could be used to separate each of the following?
- solid calcium chloride from a solution of calcium chloride in water
- the components of a solution of vinegar in water
- particulates from water in a fish tank
- Match each separation technique in (a) with the physical/chemical property that each takes advantage of in (b).
- crystallization, distillation, filtration
- volatility, physical state, solubility
- The following figures illustrate the arrangement of atoms in some samples of matter. Which figures are related by a physical change? By a chemical change?
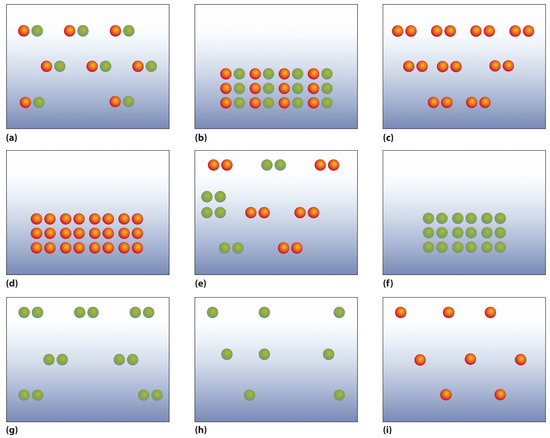
- Classify each statement as an extensive property or an intensive property.
- Carbon, in the form of diamond, is one of the hardest known materials.
- A sample of crystalline silicon, a grayish solid, has a mass of 14.3 g.
- Germanium has a density of 5.32 g/cm3.
- Gray tin converts to white tin at 13.2°C.
- Lead is a bluish-white metal.
- Classify each statement as a physical property or a chemical property.
- Fluorine etches glass.
- Chlorine interacts with moisture in the lungs to produce a respiratory irritant.
- Bromine is a reddish-brown liquid.
- Iodine has a density of 11.27 g/L at 0°C.
NUMERICAL PROBLEMS
Please be sure you are familiar with the topics discussed in Essential Skills 1 (Section 1.9) before proceeding to the Numerical Problems.
- If a person weighs 176 lb on Earth, what is his or her mass on Mars, where the force of gravity is 37% of that on Earth?
- If a person weighs 135 lb on Earth, what is his or her mass on Jupiter, where the force of gravity is 236% of that on Earth?
- Calculate the volume of 10.00 g of each element and then arrange the elements in order of decreasing volume. The numbers in parentheses are densities.
- copper (8.92 g/cm3)
- calcium (1.54 g/cm3)
- titanium (4.51 g/cm3)
- iridium (22.85 g/cm3)
- Given 15.00 g of each element, calculate the volume of each and then arrange the elements in order of increasing volume. The numbers in parentheses are densities.
- gold (19.32 g/cm3)
- lead (11.34 g/cm3)
- iron (7.87 g/cm3)
- sulfur (2.07 g/cm3)
- A silver bar has dimensions of 10.00 cm × 4.00 cm × 1.50 cm, and the density of silver is 10.49 g/cm3. What is the mass of the bar?
- Platinum has a density of 21.45 g/cm3. What is the mass of a platinum bar measuring 3.00 cm × 1.50 cm × 0.500 cm?
- Complete the following table.
Density (g/cm3) Mass (g) Volume (cm3) Element 3.14 79.904 Br 3.51 3.42 C 39.1 45.5 K 11.34 207.2 Pb 107.868 10.28 Ag 6.51 14.0 Zr - Gold has a density of 19.30 g/cm3. If a person who weighs 85.00 kg (1 kg = 1000 g) were given his or her weight in gold, what volume (in cm3) would the gold occupy? Are we justified in using the SI unit of mass for the person’s weight in this case?
- An irregularly shaped piece of magnesium with a mass of 11.81 g was dropped into a graduated cylinder partially filled with water. The magnesium displaced 6.80 mL of water. What is the density of magnesium?
- The density of copper is 8.92 g/cm3. If a 10.00 g sample is placed in a graduated cylinder that contains 15.0 mL of water, what is the total volume that would be occupied?
- At 20°C, the density of fresh water is 0.9982 kg/m3, and the density of seawater is 1.025 kg/m3. Will a ship float higher in fresh water or in seawater? Explain your reasoning.
Numerical Answers
1. Unlike weight, mass does not depend on location. The mass of the person is therefore the same on Earth and Mars: 176 lb ÷ 2.2 lb/kg = 80 kg.
3.
a. Cu: 1.12 cm3
b. Ca: 6.49 cm3
c. Ti: 2.22 cm3
d. Ir: 0.4376 cm3
Volume decreases: Ca > Ti > Cu > Ir
5. 629 g
9. 1.74 g/cm3
1.3 Problems
1. Milk turns sour. This is a ________________
- Chemical Change
- Physical Change
- Chemical Property
- Physical Property
- None of the above
2. HCl being a strong acid is a __________, Wood sawed in two is ___________
- Chemical Change, Physical Change
- Physical Change, Chemical Change
- Chemical Property, Physical Change
- Physical Property, Chemical Change
- None of the above
3. CuSO4 is dissolved in water
- Chemical Change
- Physical Change
- Chemical Property
- Physical Property
- None of the above
4. Aluminum Phosphate has a density of 2.566 g/cm3
- Chemical Change
- Physical Change
- Chemical Property
- Physical Property
- None of the above
5. Which of the following are examples of matter?
- A Dog
- Carbon Dioxide
- Ice Cubes
- copper (II) nitrate
- A Moving Car
6. The formation of gas bubbles is a sign of what type of change?
7. True or False: Bread rising is a physical property. 8. True or False: Dicing potatoes is a physical change. 9. Is sunlight matter? 10. The mass of lead is a _____________property.
1.3 Solutions
1)chemical change 2) chemical property, physical change 3) physical change 4) physical property 5) All of the above 6) chemical 7) False 8) True 9) No 10) physical property
1.6
- Write a single equation to show how to convert
- \(cm/min\) to \(km/h\);
- \(cal/oz\) to \(J/g\)
- \(lb/in^2\) to \(kg/m^2\) and
- \(°C/s\) to \(K/h\).
- How many Calories are contained in an 8.0 oz serving of green beans if their fuel value is 1.5 kJ/g?
- Gasoline has a fuel value of 48 kJ/g. How much energy in joules can be obtained by filling an automobile’s 16.3 gal tank with gasoline, assuming gasoline has a density of 0.70 g/mL?
Solutions
- Converting from one compound unit to another
- \[\left(\dfrac{\cancel{cm}}{\cancel{min}}\right)\left(\dfrac{1\;\cancel{m}}{100\; \cancel{cm}}\right)\left(\dfrac{1\; km}{1000\;\cancel{m}}\right)\left(\dfrac{60\;\cancel{min}}{1\; h}\right)= km/h \nonumber \]
- \[\left(\dfrac{\cancel{cal}}{\cancel{oz}}\right) \left(\dfrac{4.184 \;J}{1\; \cancel{cal}}\right) \left( \dfrac{16\; \cancel{oz}}{1\; \cancel{lb}}\right) \left(\dfrac{1\; \cancel{lb}}{453.59 \;g}\right)= J/g \nonumber \]
- \[\left(\dfrac{\cancel{lb}}{\cancel{in^2}}\right)\left(\dfrac{16 \;\cancel{oz}}{\cancel{lb}}\right) \left(\dfrac{28.35\; \cancel{g}}{\cancel{oz}}\right)\left(\dfrac{1\; kg}{1000\; \cancel{g}}\right) \left[\dfrac{(36\; \cancel{in.})^2}{(1\;\cancel{yd})^2}\right] \left[\dfrac{1.09 \;\cancel{yd^2}}{1 \;m^2}\right] =kg/m^2 \nonumber \]
- \[\left(\dfrac{°C}{\cancel{s}}\right)\left(\dfrac{60\;\cancel{s}}{1\;\cancel{min}}\right)\left(\dfrac{60\;\cancel{min}}{h}\right)+273.15 K = K/h \nonumber \]
- Our goal is to convert 1.5 kJ/g to Calories in 8 oz:\[\left(\dfrac{1.5 \; \cancel{kJ}}{1\; \cancel{g}}\right)\left(\dfrac{1000\; \cancel{J}}{1\; \cancel{kJ}}\right)\left(\dfrac{1\; \cancel{cal}}{4.184\; \cancel{J}}\right)\left(\dfrac{1\; Cal}{1000\; \cancel{cal}}\right)\left(\dfrac{28.35 \;\cancel{g}}{1\; \cancel{oz}}\right)\left(8.0\; \cancel{oz}\right)= 81\; Cal \nonumber \]
- Our goal is to use the energy content, 48 kJ/g, and the density, 0.70 g/mL, to obtain the number of joules in 16.3 gal of gasoline: \[\left(\dfrac{48\; \cancel{kJ}}{g}\right)\left(\dfrac{1000\; J}{\cancel{kJ}}\right)\left(\dfrac{0.70\; \cancel{g}}{\cancel{mL}}\right)\left(\dfrac{1000\; \cancel{mL}}{\cancel{L}}\right)\left(\dfrac{3.79 \;\cancel{L}}{\cancel{gal}}\right)\left(16.3 \;\cancel{gal}\right)= 2.1 \times 10^9 J \nonumber \]

