6.5: Constant Volume Calorimetry- Measuring ΔU for Chemical Reactions
- Page ID
- 38089
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Constant-pressure calorimeters are not very well suited for studying reactions in which one or more of the reactants is a gas, such as a combustion reaction. The enthalpy changes that accompany combustion reactions are therefore measured using a constant-volume calorimeter, such as the bomb calorimeter(A device used to measure energy changes in chemical processes. shown schematically in Figure \(\PageIndex{1}\)). The reactant is placed in a steel cup inside a steel vessel with a fixed volume (the “bomb”). The bomb is then sealed, filled with excess oxygen gas, and placed inside an insulated container that holds a known amount of water. Because combustion reactions are exothermic, the temperature of the bath and the calorimeter increases during combustion. If the heat capacity of the bomb and the mass of water are known, the heat released can be calculated.
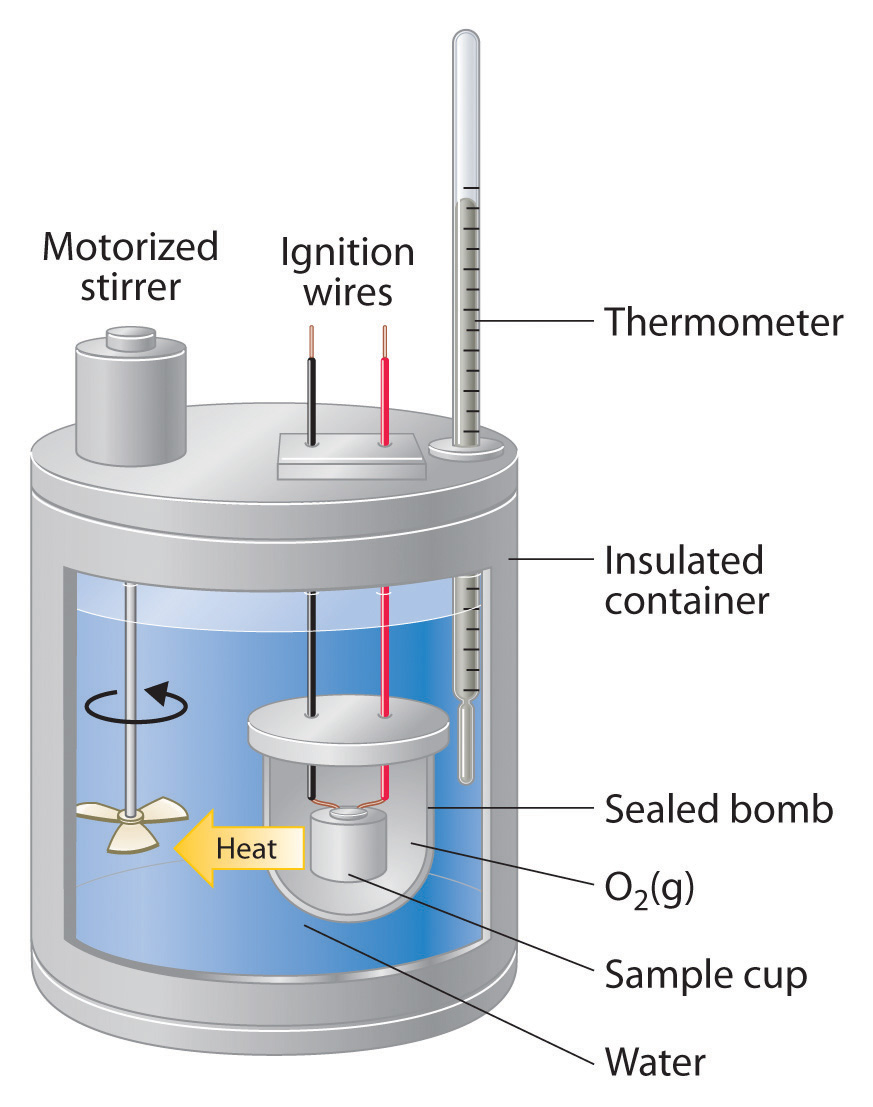
Because the volume of the system (the inside of the bomb) is fixed, the combustion reaction occurs under conditions in which the volume, but not the pressure, is constant. The heat released by a reaction carried out at constant volume is identical to the change in internal energy (ΔE) rather than the enthalpy change (ΔH); ΔE is related to ΔH by an expression that depends on the change in the number of moles of gas during the reaction. The difference between the heat flow measured at constant volume and the enthalpy change is usually quite small, however (on the order of a few percent). Assuming that ΔE < ΔH, the relationship between the measured temperature change and ΔHcomb is given in Equation \(\ref{5.5.9}\), where Cbomb is the total heat capacity of the steel bomb and the water surrounding it:
\[ \Delta H_{comb} < q_{comb} = q_{calorimater} = C_{bomb} \Delta T \label{5.5.9}\]
To measure the heat capacity of the calorimeter, we first burn a carefully weighed mass of a standard compound whose enthalpy of combustion is accurately known. Benzoic acid (C6H5CO2H) is often used for this purpose because it is a crystalline solid that can be obtained in high purity. The combustion of benzoic acid in a bomb calorimeter releases 26.38 kJ of heat per gram (i.e., its ΔHcomb = −26.38 kJ/g). This value and the measured increase in temperature of the calorimeter can be used in Equation \(\ref{5.42}\) to determine Cbomb. The use of a bomb calorimeter to measure the ΔHcomb of a substance is illustrated in Example \(\PageIndex{4}\).
Example \(\PageIndex{4}\): Combustion of Glucose
The combustion of 0.579 g of benzoic acid in a bomb calorimeter caused a 2.08°C increase in the temperature of the calorimeter. The chamber was then emptied and recharged with 1.732 g of glucose and excess oxygen. Ignition of the glucose resulted in a temperature increase of 3.64°C. What is the ΔHcomb of glucose?
Given: mass and ΔT for combustion of standard and sample
Asked for: ΔHcomb of glucose
Strategy:
- Calculate the value of qrxn for benzoic acid by multiplying the mass of benzoic acid by its ΔHcomb. Then use Equation \(ref{5.5.9}\) to determine the heat capacity of the calorimeter (Cbomb) from qcomb and ΔT.
- Calculate the amount of heat released during the combustion of glucose by multiplying the heat capacity of the bomb by the temperature change. Determine the ΔHcomb of glucose by multiplying the amount of heat released per gram by the molar mass of glucose.
Solution:
The first step is to use Equation \(\ref{5.5.9}\) and the information obtained from the combustion of benzoic acid to calculate Cbomb. We are given ΔT, and we can calculate qcomb from the mass of benzoic acid:
\[ q{comb} = \left ( 0.579 \; \cancel{g} \right )\left ( -26.38 \; kJ/\cancel{g} \right ) = - 15.3 \; kJ \]
From Equation \(\ref{5.5.9}\),
\[ -C{bomb} = \dfrac{q_{comb}}{\Delta T} = \dfrac{-15.3 \; kJ}{2.08 \; ^{o}C} =- 7.34 \; kJ/^{o}C \]
B According to the strategy, we can now use the heat capacity of the bomb to calculate the amount of heat released during the combustion of glucose:
\[ q_{comb}=-C_{bomb}\Delta T = \left ( -7.34 \; kJ/^{o}C \right )\left ( 3.64 \; ^{o}C \right )=- 26.7 \; kJ \]
Because the combustion of 1.732 g of glucose released 26.7 kJ of energy, the ΔHcomb of glucose is
\[ \Delta H_{comb}=\left ( \dfrac{-26.7 \; kJ}{1.732 \; \cancel{g}} \right )\left ( \dfrac{180.16 \; \cancel{g}}{mol} \right )=-2780 \; kJ/mol =2.78 \times 10^{3} \; kJ/mol\]
This result is in good agreement (< 1% error) with the value of ΔHcomb = −2803 kJ/mol that calculated using enthalpies of formation.
Exercise \(\PageIndex{4}\): Combustion of Benzoic Acid
When 2.123 g of benzoic acid is ignited in a bomb calorimeter, a temperature increase of 4.75°C is observed. When 1.932 g of methylhydrazine (CH3NHNH2) is ignited in the same calorimeter, the temperature increase is 4.64°C. Calculate the ΔHcomb of methylhydrazine, the fuel used in the maneuvering jets of the US space shuttle.
Answer
−1.30 × 103 kJ/mol

