These are homework exercises to accompany the Textmap created for Chemistry: A Molecular Approach by Nivaldo Tro. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.
Q1.35
A household receives a $125 electricity bill. The cost of electricity is $0.150 /kWh. How much energy, in joules (J), did the household use?
Strategy
Step 1: You must first multiply the total cost of the bill ($125) by 1 kWh and then divide that answer by the cost of each kW ($0.150 kWh). You should end up with an equation that looks like this:
\[($125)\times \dfrac{1\;kWh}{0.150\;kWh}\nonumber \]
Step 2: Once you do this math, then you should receive the answer of 833.33 kWh. This is the number of kWh used during the billing cycle.
Step 3: Next, you will then take your solution found during step 1 and multiply it by \(\dfrac{1}{2.78\times 10^{-7}}\) in order to convert kWh to kWh/J. You should have the equation:
\[(833.33)\times \dfrac{1}{2.78\cdot 10^{-7}}\nonumber \]
Step 4: After completing step 3, you should receive an answer of \[3.0 \times 10^{9} J\nonumber \]
Step 5: YOU ARE FINISHED!
Q1.36
Determine whether the mixtures are Homogeneous or Heterogeneous. State whether it is a compound or pure substance?
- Mud and Water
- Salt and water
- Chicken noodle soup
- Gold
- \(H_{2}O\)
Strategy
- Homogeneous: mixtures are uniformly distributed, easily dissolved, of a single phase, also they are easily dispersed through the membrane.
- Heterogeneous: mixtures are unequally distributed, do not dissolve in water, and could be of different phases. A pure substance: has a definite and constant composition, it can be a compound or and element.
- A element: is composed of a single atom.
- A compound is composed of two or more elements. For example, \(H_{2}O\) is a ratio of two hydrogen atoms and one oxygen atom to form \(H_{2}O\). So with this strategy you can solve the following question.
- Mud and Water: Heterogeneous mixture
- Salt and water: Homogeneous mixture
- Chicken noodle soup: Heterogeneous mixture
- Gold: (element)
- \(H_{2}O\): Compound
Q1.36
Classify each substance as a pure substance or a mixture. If it is a pure substance, classify it as an element or a compound. If it is a mixture, classify it as homogeneous or heterogeneous.
- Plain yogurt
- Chicken noodle soup
- Titanium
- Table salt
What we know:
- A pure substance is made up of only one type of particle.
- A mixture is a substance composed of two or more particles.
- An element is a substance that cannot be chemically broken down into simpler substances.
- A compound is a substance composed of two or more elements.
- A heterogeneous mixture is one in which the composition varies from one region of the mixture to another.
- A homogeneous mixture is one with the same composition throughout.
Solution
- mixture, homogeneous
- mixture, heterogeneous
- pure substance, element
- pure substance, compound
Q1.41
Classify Each statement as an Observation, Theory, or Law.
- All matter that exists is made up of Submicroscopic particles known as atoms.
- If an iron rod is placed in a closed container and it rusts, the mass of the container and its contents do not change.
- Matter is neither created nor destroyed
- When a candle is burned, heat is released
Strategy
You need to understand what an Observation, Theory or law is before you classify it in the question.
- Observation: An outcome of events that is being viewed
- Theory: Preserved explanation for observations and laws
- Law: Summarizes past observations and predicts future ones
Now that we have defined them, we need to apply it to the question (AnswerS IN BOLD)
- This statement is proposing all matter is made up of atoms so it would become a theory because it is an idea that studies propose is true.
- This statement is saying, without matter being added to the container, As you See it rust, the mass doesn't change so this is assumed by Observation.
- This statement is called the Law of conservation of mass, so because this is true, the statement is a Law.
- If you are looking at a candle and see the flame, then you should understand that heat is being released. You tell this from Observation.
Q1.45
When 12 g of sodium reacts with 23.5 g of chlorine to form sodium chloride, how many grams of sodium chloride is formed? (Assume that sodium chloride is the only product).
Solution:
What we know: We have a chemical reaction between sodium and chlorine to form only sodium chloride. We are also given the masses of the reactants, 12 g of sodium and 23.5 g of chlorine. We also know that the Law of Conservation of Mass tells us that matter is neither created nor destroyed in a chemical reaction.
What we're asked for: The mass, in grams, of sodium chloride formed from the reaction.
Strategy:
A. Find the sum of the masses of the reactants from the chemical equation.
Solution
12 g + 23.5 g = 35.5 g
35.5 g of sodium chloride is formed from the reaction.
Q1.55
According to Dalton's Atomic Theory, what are compounds made up of?
Strategy
- Find the summary of Dalton's Atomic Theory
- Read through it
- Locate where it talks about what compounds are made of
- Write your answer
Solution
Compounds are made up of two or more different atoms.
Q1.64
Isotopes are atoms that have the same number of protons but differ in the number of neutrons. Write the chemical symbols for each of the following isotopes:
- the chlorine isotope with 18 neutrons
- the chlorine isotope with 20 neutrons
- the calcium isotope with 20 neutrons
- the neon isotope with 11 neutrons
Strategy:
- Determine the given element's atomic number from the periodic table.
- Add the number of neutrons given in the question to the atomic number to calculate the mass number of the isotope.
- The mass number will be represented in the upper left corner of the chemical symbol, while the atomic number will be represented in the lower left corner.
Helpful Hints:
- A chemical symbol is written as \[_{Z}^{A}\textrm{X}\nonumber \] . The A stands for the number of protons and neutrons, also known as the mass number. The Z stands for the number of protons, also known as the atomic number.
- Subtracting Z from A will give you the number of neutrons. Example: \[_{19}^{39}\textrm{K}\nonumber \] --> 39-19= 20 neutrons
- Therefore, adding the given number of neutrons to the atomic number, Z, gives you the mass number.
Solution:
- \[_{17}^{35}\textrm{Cl}\nonumber \]
- \[_{17}^{37}\textrm{Cl}\nonumber \]
- \[_{20}^{40}\textrm{Ca}\nonumber \]
- \[_{10}^{21}\textrm{Ne}\nonumber \]
Q1.65
Give the number of protons and neutrons in each isotope listed
- \[_{19}^{41}\textrm{K}\nonumber \]
- \[_{4}^{11}\textrm{Be}\nonumber \]
- \[_{22}^{45}\textrm{Ti}\nonumber \]
- \[_{8}^{16}\textrm{O}\nonumber \]
Strategy
Take the larger number and subtract the smaller number from it. The smaller number is the atomic number (z), which indicates the number of protons the element has. The larger number indicates the number of protons and neutron present in the element.
- 41K has an atomic mass of 41. The atomic mass is the number of protons and neutrons present in the element. To get the number of neutrons, subtract the atomic number (19) from the atomic mass (41). When done so you find that K41 has 19 protons and 22 neutrons. Keep in mind the atomic number is the number of protons present in the element, so the only thing you are trying to find through subtraction is the number of neutrons.
- For 11Be, the same thing occurs. Take the atomic number and subtract it from the atomic mass. The atomic mass is 11 and the atomic number is 4, so, 11 minus for equals 7. The answer for part b. is 4 protons and 7 neutrons.
- For 45 Ti, you subtract 22 from 45, which gives you 22 protons and 23 neutrons.
- For 16O, the same method is applied. Subtract 8 from 16 and you get 8 protons and 8 electrons.
Q1.66
Question: Find the amount of protons and neutrons in the following atoms:
- \[_{6}^{14}\textrm{C}\nonumber \]
- \[_{8}^{18}\textrm{O}\nonumber \]
- \[_{25}^{55}\textrm{Mn}\nonumber \]
- \[_{30}^{64}\textrm{Zn}\nonumber \]
Strategy
- First identify the subscript, the bottom number on the left hand side of the element's symbol. This is the atomic number and indicates how many protons the atom's nucleus contains. All isotopes of the same element contain the same number of protons.
- Next, identify the superscript, the top number left hand side of the element symbol. This is the atomic mass number, the total combined number of protons and neutrons. Different isotopes of a given element differ in the number of neutrons contained in their nuclei.
- The number of protons can be found simply by identifying the atomic number. To find the number of neutrons in the atom, the atomic number is subtracted from the atomic mass number.
Solution
A The atomic number of carbon is 6, the atomic number of oxygen is 8, the atomic number of manganese is 25, and the atomic number of zinc is 30. Therefore, we now know the number of protons contained within each atom since this number is represented by the atomic number.
B The atomic mass number of the carbon isotope is 14, the mass number of the oxygen isotope is 18, the mass number of the manganese isotope is 55, and the mass number of the zinc isotope is 64. This is the combined number of protons and neutrons in each respective isotope.
C Carbon isotope: \[14-6=8\, neutrons\nonumber \]
Oxygen isotope: \[18-8=10\, neutrons\nonumber \]
Manganese isotope: \[55-25=30\, neutrons\nonumber \]
Zinc isotope: \[64-30=34\, neutrons\nonumber \]
Q1.64
Write the isotopic symbols in the form \(\ce{^A_ZX}\) for each isotope.
- The oxygen isotope with 9 neutrons.
- The neon isotope with 10 neutrons.
- The chlorine isotope with 18 neutrons.
- The carbon isotope with 8 neutrons.
Strategy
- Identify each element’s atomic number (number of protons).
- Find the atomic mass of each element by adding the number of protons and the number of neutrons.
- Properly write the isotopic symbol of each element by placing the atomic mass as the superscript and the atomic number (number of protons) as the subscript.
Solution
- Atomic Numbers (Number of Protons):
Oxygen: 8 protons
Neon: 10 protons
Chlorine: 17 protons
Carbon: 6 protons
- Atomic Mass:
Oxygen: 8+9=17
Neon: 10+10=20
Chlorine: 17+18=35
Carbon: 6+8=14
- Isotopic Symbols:
Oxygen: 178O
Neon: 2010Ne
Chlorine: 3517Cl
Carbon: 146C
Q1.69
Question: Determine the number of protons and electrons in each of the following ions.
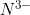
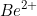
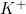
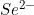
Strategy
- First locate each element on the periodic table. Identify the atomic number associated with each element, or the number in between the element's symbol and scientific name. The atomic number is the number of protons as well as the number of electrons an element possesses in it's neutral state.
- Next, identify the superscript of each element, or the number to the top right of the element's symbol. This number should include a "+" or "-" sign next to it, indicating the element's charge. A "+" indicates a positively charged ion and a "-" indicates a negatively charged ion. An element becomes positively charged when it loses electrons, and negative when it gains electrons.
- To solve for each element's total number of electrons, take that element's atomic number, and inversely add or subtract the number in the superscript according to the element's charge. If an element has a "+" sign, it is losing the amount of electrons indicated by the superscript number, so subtract this number from the element's atomic number. The same goes if an element has a "-" sign, instead adding the number in the superscript to the element's atomic number.
Solution
(1) N3-
A. Nitrogen's atomic number is 7, so in a neutral state, Nitrogen has 7 protons and electrons.
B. Nitrogen's superscript is "3-" indicating that it is gaining 3 electrons
C. Because it gains 3 electrons, N3- now has a total of 10 electrons.
(2) Be2+
A. Beryllium's atomic number is 4, so Beryllium possesses 4 protons and electrons
B. The superscript "2+" indicates beryllium is losing 2 electrons
C. 2 electrons are subtracted from Beryllium's total 4, so it now has 2 electrons.
(3) K+
A. Potassium as a neutral element possesses 19 protons and electrons, indicated by it's atomic number of 19.
B. The superscript "+" indicates Potassium will lose 1 electron from it's total.
C. 19 total electrons minus 1 makes K+ number of electrons to 18.
(4) Se2-
A. Selenium's atomic number is 34, indicating 34 protons and electrons at ground state.
B. It' superscript "2-" indicates that it will be gaining 2 electrons to it's total.
C. 34 electrons plus 2 makes selenium's total number of electrons 34.
Q 1.73
The atomic mass for Helium is 4.003 amu and the mass spectrum for Helium shows a spike at this mass. Meanwhile, the atomic mass for Bromine is 79.904 amu; however, the mass spectrum for Bromine does not show a peak at that mass. What causes the difference?
Solution
- The best way to start this problem is to recall what the atomic mass means in the context of the problem. This is the standard atomic mass, which is the weighted average of all the isotopes. "Weighted" in this situation means that the abundance of each isotope factors in to how it factors in to the overall the standard atomic mass for that particular element.
- Next step is to look at Helium. Helium has two isotopes and is stable at either; however, in atmospheric values, Helium is found most abundantly as 4He (99.999863%) and much less commonly found as 3He (0.000137%). Consequently, 3He does not have a strong influence on the standard atomic mass of Helium or much expression on the mass spectrum which measures relative abundance.
- Examining Bromine reveals two major isotopes for that element as well. Both 79Br as well as 81Br are rather prevalent (79Br with 50.69% and 81Br with 49.31%). This means that their relative abundance is high enough that they would make a significant impact on both the mass spectrum as well as the standard atomic weight of Bromine.
- To connect the dots, the dichotomy between the two elements comes from the abundance of their isotopes. Bromine's two isotopes almost equally comprise the atomic mass so the atomic mass they produce does not match up with an actual relatively abundant isotope of Br so therefore the line for that particular atomic mass is absent on the mass spectrum for Br. Helium, meanwhile, is primarily influenced by the 3He because of its incredibly high abundance and therefore the mass spectrum and the standard atomic mass are very similar.
Q1.74
The atomic mass of chlorine is 35.453 amu. There are two stable isotopes for chlorine. Would either of these isotopes have a mass of 35.453 amu? Why or why not?
Important things to consider
- The atomic mass is the sum of the protons and neutrons.
- Isotopes vary in the amount of neutrons of the same element.
- Each isotope will have a different mass number depending upon how many neutrons are present.
- amu = atomic mass unit
- unit used for indicating mass on an atomic scale
Answer
No, because isotopes are variants of an element that differ in the number of neutrons present, but they have the same number of protons (atomic number the same).

