1.2: Isotopes

Last updated
Save as PDF

Page ID: 46526

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Although all atoms of an element have the same number of protons, the atoms may differ in the number of neutrons they have (Table 1-2). These differing atoms of the same element are called isotopes. Four isotopes of helium (He) are shown in Figure 1-1. All atoms of chlorine (Cl) have 17 protons, but there are chlorine isotopes having 15 to 23 neutrons. Only two chlorine isotopes exist in significant amounts in nature, those with 18 neutrons (75.53% of all chlorine atoms found in nature), and those with 20 neutrons (24.47%). To write the symbol for an isotope, place the atomic number as a subscript and the mass number (protons plus neutrons) as a superscript to the left of the atomic symbol. 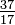The symbols for the two naturally occurring isotopes of chlorine then would be $\textstyle{\frac{35}{17}}$ Cl and $\textstyle{\frac{37}{17}}$ Cl. Strictly speaking, the subscript is unnecessary, since all atoms of chlorine have 17 protons. Hence the isotope symbols are usually written without the subscript: ³⁵Cl and ³⁷Cl. In discussing these isotopes, we use the. terms chlorine-35 and chlorine-37. For a nucleus to be stable, the number of neutrons should (for the first few elements) equal or slightly exceed the number of protons. The more protons, the greater the ratio of neutrons to protons to ensure stability. Nuclei that have too many of either kind of fundamental particle are unstable, and break down radioactively in ways that are discussed in Chapter 23.

Figure 1-1 Four isotopes of helium (He). All atoms of helium have two protons (hence two electrons), but the number of neutrons can vary. Most helium atoms in nature have two neutrons (helium-4), and fewer than one helium atom per million in nature has just one neutron (helium-3). The other helium isotopes, helium-5, helium-6, and helium-8 (not shown) are unstable and are seen only briefly in nuclear reactions (see Chapter 23). The size of the nucleus is grossly exaggerated here. If the nucleus were of the size shown, the atom would be half a kilometer across.

Example 1.2.1

How many protons, neutrons, and electrons are there in an atom of the most stable isotope of uranium, uranium-238? Write the symbol for this isotope. Refer to Figure. 1-1.

Solution

The atomic number of uranium (see the inside back cover) is 92, and the mass number of the isotope is given as 238. Hence it has 92 protons, 92 electrons,and 238 - 92 = 146 neutrons. Its symbol is $\textstyle{\frac{238}{92}}$ U (or ²³⁸U).

The total mass of an atom is called its atomic weight, and this is almost but not exactly the sum of the masses of its constituent protons, neutrons and electrons. * When protons, neutrons, and electrons combine to form an atom, some of their mass is converted to energy and is given off. (This is the source of energy in nuclear fusion reactions.) Because the atom cannot be broken down into its fundamental particles unless the energy for the missing mass is supplied from outside it, this energy is called the binding energy of the nucleus.

Note: Atomic Weight vs. Atomic Mass

The terms atomic weight and molecular weight are universally used by working scientists, and will be used in this book, even though these are technically masses rather than weights.

**Table 1-2. Composition of Typical Atoms and Ions**
	Electrons	Protons	Neutrons	Atomic Number	Atomic Weight (amu)	Total Charge (electron units)
Hydrogen atom, ¹H or H	1	1	0	1	1.008	0
Deuterium atom, ²H or D	1	1	1	1	2.014	0
Tritium atom, ³H or T	1	1	2	1	3.016	0
Hydrogen ion, H⁺	0	1	0	1	1.007	+1
Helium atom, ⁴He	2	2	2	2	4.003	0
Helium nucleus or alpha particle, He²⁺ or α	0	2	2	2	4.002	+2
Lithium atom, ⁷Li	3	3	4	3	7.016	0
Carbon atom, ¹²Ca	6	6	6	6	12.000	0
Oxygen atom, ¹⁶O	8	8	8	8	15.995	0
Chlorine atom, ³⁵Cl	17	17	18	17	34.969	0
Chlorine atom, ³⁷Cl	17	17	20	17	36.966	0
Naturally occurring mixture of chlorine	17	17	18 or 20	17	35.453	0
Uranium atom, ²³⁴U	92	92	142	92	234.04	0
Uranium atom, ²³⁵U	92	92	143	92	235.04	0
Uranium atom, ²³⁸U	92	92	146	92	238.05	0
Naturally occurring mixture of uranium	92	92	varied	92	238.03	0

Example 1.2.2

Calculate the mass that is lost when an atom of carbon-12 is formed from protons, electrons, and neutrons.

Solution

Since the atomic number of every carbon atom is 6, carbon-12 has 6 protons and therefore 6 electrons. To find the number of neutrons, we subtract the number of protons from the mass number: 12 - 6 = 6 neutrons. We can use the data in Table 1-1 to calculate the total mass of these particles:

Protons:	6 X 1.00728 amu = 6.04368 amu
Neutrons:	6 X 1.00867 amu = 6.05202 amu
Electrons:	6 X 0.00055 amu = 0.00330 amu
	Total particle mass: 12.09900 amu

But by the definition of the scale of atomic mass units, the mass of one carbon-12 atom is exactly 12 amu. Hence 0.0990 amu of mass has disappeared in the process of building the atom from its particles.

Example 1.2.3

Calculate the expected atomic weight of the isotope of chlorine that has 20 neutrons. Compare this with the actual atomic weight of this isotope as given in Table 1-2.

Solution

The chlorine isotope has 17 protons and 20 neutrons:

Protons:	17 X 1.00728 amu =	17.1238 amu
Neutrons:	20 X 1.00867 amu =	20.1734 amu
Electrons:	17 X 0.00055 amu =	0.0094 amu
	Total particle mass:	37.3066 amu
	Actual observed atomic weight:	36.966 amu
	Mass Loss:	0.341 amu

Each isotope of an element is characterized by an atomic number (total number of protons), a mass number (total number of protons and neutrons), and an atomic weight (mass of atom in atomic mass units). Since mass losses upon formation of an atom are small, the mass number is usually the same as the atomic weight rounded to the nearest integer. (For example, the atomic weight of chlorine-37 is 36.966, which is rounded to 37.) If there are several isotopes of an element in nature, then of course the experimentally observed atomic weight (the natural atomic weight) will be the weighted average of the isotope weights. The average is weighted according to the percent abundance of the isotopes. Chlorine occurs in nature as 75.53% chlorine-35 (34.97 amu) and 24.47% chlorine-37 (36.97 amu), so the weighted average of the isotope weights is

\[(0.7553 \times 34.97 \;amu) + (0.2447 \times 36.97\; amu) = 35.46\; amu\]

The atomic weights given inside the back cover of this book are all weighted averages of the isotopes occurring in nature, and these are the figures we shall use henceforth-unless we are specifically discussing one isotope. All isotopes of an element behave the same way chemically for the most part. Their behavior will differ in regard to mass-sensitive properties such as diffusion rates, which we'll look at later in this book.

Example 1.2.4

Magnesium (Mg) has three significant natural isotopes: 78.70% of all magnesium atoms have an atomic weight of 23.985 amu, 10.13% have an atomic weight of 24.986 amu, and 11.17% have an atomic weight of 25.983 amu. How many protons and neutrons are present in each of these three isotopes? How do we write the symbols for each isotope? Finally, what is the weighted average of the atomic weights?

Solution

There are 12 protons in all magnesium isotopes. The isotope whose atomic weight is 23.985 amu has a mass number of 24 (protons and neutrons), so 24 - 12 protons gives 12 neutrons. The symbol for this isotope is 24Mg. Similarly, the isotope whose atomic weight is 24.986 amu has a mass number of 25, 13 neutrons, and 25Mg as a symbol. The third isotope (25.983 amu) has a mass number of 26, 14 neutrons, and 26Mg as a symbol. We calculate the average atomic weight as follows:

(0.7870 X 23.985) + (0.1013 X 24.986) + (0.1117 X 25.983) = 24.31 amu

Example 1.2.5

Boron has two naturally occurring isotopes, ^lOB and ¹¹B. We know that 80.22% of its atoms are ¹¹B, atomic weight 11.009 amu. From the natural atomic weight given on the inside back cover, calculate the atomic weight of the ^lOB isotope.

Solution

If 80.22% of all boron atoms are ¹¹B, then 100.00 - 80.22, or 19.78%, are the unknown isotope. We can use W to represent the unknown atomic weight in our calculation:

(0.8022 X 11.009) + (0.1978 X W) = 10.81 amu (natural atomic weight)

W =

\textstyle{\frac{10.81-8.831}{0.1978}}

= 10.01 amu

Contributors and Attributions

R. E. Dickerson, H. B. Gray, and G. P. Haight, Jr. Content was used from "Chemical Principles", an introductory college-level text for General Chemistry with permission of the Caltech library and Harry B. Gray, on behalf of the authors.

Search

Text Color

Text Size

Margin Size

Font Type