18.10: The Effect of Temperature
- Page ID
- 49617
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The fact that a small increase in temperature can double the rate of a reaction is primarily dependent on an observation we made in the section on molecular speed distribution. A seemingly minor temperature rise causes a major increase in the number of molecules whose speeds (and hence molecular energies) are far above average. This happens because the distribution of molecular speeds (figure 2 in the section on molecular speed distribution) is lopsided and tails off very slowly at the high-speed end. Since only those molecules whose energy exceeds the activation energy can react, a significant increase in the fraction of molecules having high energy causes a significant increase in rate.
The fraction of molecules which have enough kinetic energy to react depends on the activation energy E‡, the temperature T, and the gas constant R in the following way:
Fraction of molecules having enough energy to react
\[= e^{\frac {-E^ \pm}{RT}}\label{1} \]
\[= 10^{\frac {-E^\pm}{2.303RT}}\label{2} \]
Although a derivation of this result is beyond the scope of our current discussion, we can look at this equation to see that it agrees with common sense. The larger the E‡, the more negative the exponent, and the smaller the fraction of molecules which can react. Thus if two similar reactions are studied under the same conditions of temperature and concentration, the one with the larger activation energy is expected to be slower. As a corollary to this, if we can find some way to reduce the activation energy of a particular reaction, then we can get that reaction to go faster. Equations \(\ref{1}\) and \(\ref{2}\) also shows why changing the temperature has such a large effect on reaction rates. Increasing T decreases the magnitude negative exponent in the equation. This increases the fraction of molecules which can react, as shown by the following example:
The reaction
\[\ce{CO + NO2 -> CO2 +NO} \nonumber \]
has an activation energy of 116 kJ mol. Calculate the fraction of molecules whose kinetic energies are large enough that they can collide with sufficient energy to react (a) at 298 K, and (b) at 600 K.Solution
In both cases we use Eq. \(\ref{2}\).
a) At 298 K, the power of 10 will be- \(\dfrac{-E^\pm}{2.303RT}=\dfrac{-116 \frac{kJ}{mol}}{2.303 * 8.314 \dfrac{J}{K*mol} * 298K}\)
-
-
-
- \(=\dfrac{-116 \dfrac{kJ}{mol}}{2.303 * 8.314 \dfrac{J}{K*mol} * 298K}=-20.3\)
-
-
-
- \(Fraction = 10^{-20.3} = 5.0 * 10^{-21}\)
b) At 600 k,
-
- \(Fraction = 10 ^{\dfrac{-E^{\pm}}{2.303RT}} = 10^{-10.1} = 8.0 * 10^{-11} \)
-
- \(Fraction = 10 ^{\dfrac{-E^{\pm}}{2.303RT}} = = e^{\dfrac{-E^{\pm}}{RT}} = e^{-23.25} = 8.0 * 10^{-11}\)
In this case approximately doubling the temperature causes the fraction of molecular collisions which can result in reaction to increase by a factor of
that is, by about 16 billion. This means that the reaction is expected to be about 16 billion times faster at the higher temperature. This corresponds to slightly more than doubling the rate for each of the 30 intervals of 10 K between 298 and 600 K.
Equation \(\ref{1}\) is also useful if we want to measure the activation energy of a reaction experimentally because it shows how the rate constant should vary with temperature. We have already seen that the rate of a unimolecular process should be proportional to the concentration of reactant. If only a fraction of those reactant molecules have enough energy to overcome the activation barrier, then the rate should also be proportional to that fraction. Thus we can write
-
- \[\text{Rate} = k(c_A) = k'10^{\frac{-E^{\pm}}{2.303RT_{(c_A)}}} \nonumber \]
From this equation it is clear that
-
- \[k = k'10^{\frac{-E^{\pm}}{2.303RT}} \nonumber \]
If we divide both sides by the units per second so that we can take logs, we obtain
-
- \[log \frac{k}{1 \frac{1}{s}}= log \frac{k'}{1 \frac{1}{s}} - (\frac {-E^{\pm}}{2.303RT}) \nonumber \]
\(log \frac{k}{1 \frac{1}{s}} = (\frac {-E^{\pm}}{2.303R}) * (\frac {1}{T}) + log \frac{k'}{1 \frac{1}{s}} \)
y = m * x + b
This is the standard form for the equation of a straight line whose slope m is –E‡/2.303RT and whose intercept b is log (k′/s–1). Thus if we plot log (k′/s–1) versus 1/T and a straight line is obtained, we can determine E‡.
A similar situation applies to the second-order rate equation associated with a bimolecular process, where
-
- \[\text{Rate} = K(c_A)(c_B) = k'10^{\frac{-E^{\pm}}{2.303RT}}(c_A)(c_B) \nonumber \]
In this case the rate constant has units cubic decimeter per mole per second, and so we must divide by these before taking logs. The equation that is obtained is
Again E‡ can be obtained from the slope, provided a straight-line plot is obtained. An example of such a plot for the reaction
-
- \[\ce{2HI -> H2 + I2} \nonumber \]
is shown in Figure \(\PageIndex{1}\). From its slope we can determine that E‡ = 186 kJ mol–1. This means of determining activation energy was first suggested in 1889 by Svante Arrhenius and is therefore called an Arrhenius plot.
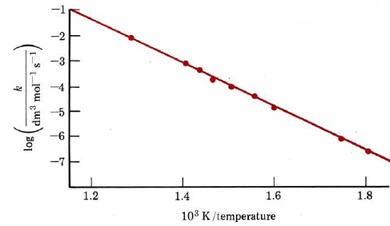
It should be pointed out that the equations just derived for Arrhenius plots apply strictly to unimolecular and bimolecular elementary processes. If a reaction mechanism involves several steps, there is no guarantee that the same elementary process will be rate limiting at several widely different temperatures. The observed rate constant may also be a product of several constants, as in the H2 + I2 reaction (Equation 5 in the section on Reaction Mechanisms). If either a different rate-limiting step or the product of constants has a different temperature dependence, then an Arrhenius plot may not be linear. This also makes it dangerous to use such a plot to predict reaction rates at temperatures quite different from the conditions under which experimental measurements were made. The slope and y-intercept of an Arrhenius plot can be used to determine the values for the Arrhenius Equation.
\[k= Ae^{\frac{-E_a}{RT}} \nonumber \]
where A is called the frequency factor, Ea is the activation energy, R is the gas law constant and T is the temperature in Kelvin. The frequency factor value depends on how often molecules collide and how orientation of the molecules is related to the reaction. A benefit of the Arrhenius equation is that it gives a direct method for computing the dependence of the rate constant, k, on temperature.




