16.3: Atoms, Molecules, and Probability
- Page ID
- 49561
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)On a microscopic level we can easily explain why some processes occur of their own accord while others do not. A spontaneous process corresponds to rearrangement of atoms and molecules from a less-probable situation to a more-probable one. A nonspontaneous process, by contrast, corresponds to movement from a probable situation to an improbable one.
An example of what probability has to do with spontaneity is provided by expansion of a gas into a vacuum. Let us calculate the probability that the process of gas expansion from flask A into a connected flask B will reverse itself, that is, the probability that the gas molecules will all collect again in flask A. If we choose a particular molecule and label it number 1, we find that it is sometimes in flask A and sometimes in flask B. Since the molecule’s motion is random and the two flasks contain the same volume, the molecule should spend half its time in each container. The probability of finding molecule 1 in container A is therefore 1/2.

Next let us consider the probability that two molecules, labeled 1 and 2, are both in flask A. Figure \(\PageIndex{1}\) shows the four possible ways these two molecules can be arranged in the two flasks. All four are equally likely, but only one has both molecules in flask A. Thus there is one chance in four that molecules 1 and 2 are both in flask A. This probability of 1/4 equals 1/2 × 1/2; i.e., it is the product of the probability that molecule 1 was in flask A times the probability that molecule 2 was in flask A. By a similar argument we can show that the probability that three given molecules are all in flask A is 1/2 × 1/2 × 1/2 = (1/2)3=1/8, and, in general, that the probability of all N gas molecules being in flask A at once is (1/2)N.
If we had 1 mol gas in the flasks, there would be 6.022 × 1023 molecules. The probability p that all of them would be in flask A at the same time would be
\[p=\left( \frac{\text{1}}{\text{2}} \right)^{\text{6}\text{.022 }\times \text{ 10}^{\text{23}}}=\frac{\text{1}}{\text{2}^{\text{6}\text{.022 }\times \text{ 10}^{\text{23}}}}=\frac{\text{1}}{\text{10}^{\text{1}\text{.813 }\times \text{ 10}^{\text{23}}}} \nonumber \] This unimaginably small number could be written as 0.000 000 . . . , where there would be 1.813 × 1023 zeros and then a 1. It would take over a thousand million million years to write that many zeros! Because there are so many molecules in a mole of gas (or any other macroscopic quantity), the probability that the spontaneous expansion will reverse itself is inconceivably small. The reversal is so improbable as to be impossible in any practical sense.
Similar remarks apply to the probability of reversing other spontaneous processes. In Figure \(\PageIndex{2}\)a, some of the atoms in a bar of metal at uniform temperature will be vibrating more than others, but the unusually energetic atoms will be distributed fairly evenly throughout the bar.
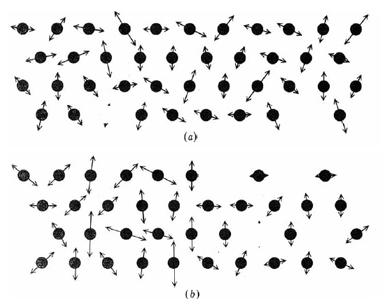
We will not suddenly find all the energetic metal atoms on the left end of the bar and all the weakly vibrating ones on the right, as in Figure \(\PageIndex{2}\)b. The possibility exists that a freak series of collisions between vibrating atoms might produce a high concentration of energetic atoms on the left, but such an occurrence is inconceivably improbable.
When a falling book hits the floor, its kinetic energy is converted to heat energy. The floor warms up slightly, and the molecules there start vibrating a little more energetically. For such a process to reverse itself spontaneously, all the floor molecules under the book would suddenly have to become more energetic and vibrate in unison in a vertical direction, flinging the book into the air. As in the previous two examples, this would require a freak series of molecular collisions which is so improbable as never to occur in the entire lifetime of the universe.
These principles also apply to the processes considered in the section on spontaneous processes. In the NI3 reaction, all of the particles distributed in the explosion would all have to return back to the ring stand and reassemble themselves. Even leaving the chemical reaction unconsidered for the moment, this return of all the particles is highly improbable.
A similar argument can be put forward for the un-mixing of the dye. The probability that all of the dye molecules will return back to a single uniform drop separate from the water at one moment is another situation so improbable that it will never happen.
Simple cases we have described show how spontaneous and nonspontaneous processes can be considered from a microscopic and statistical viewpoint. In any real sample of matter there are a great many molecules jostling each other about, exchanging energy, and sometimes exchanging atoms. This constant jostle is like shuffling a gigantic deck of cards. Because the numbers involved are so large, the laws of probability are inexorable. Some probabilities are large enough to be virtual certainties, while others are small enough to be unthinkable. Invariably the reversal of a spontaneous process turns out to involve movement from an almost certain situation to one which is unimaginably improbable. Conversely, a spontaneous process occurs when a sample of matter finds itself momentarily in a highly improbable situation. As fast as possible, it will adjust on the molecular level until maximum probability is attained.


