14.10.1: Foods- Acid Value and the Quality of Fats and Oils
- Page ID
- 50899
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The acid value (AV) is a common parameter in the specification of fats and oils. It is defined as the weight of KOH in mg needed to neutralize the organic acids present in 1g of fat and it is a measure of the free fatty acids (FFA) present in the fat or oil. An increment in the amount of FFA in a sample of oil or fat indicates hydrolysis of triglycerides (Structure on the left). Such reaction occurs by the action of lipase enzyme and it is and indicator of inadequate processing and storage conditions (i.e., high temperature and relative humidity, tissue damage). The source of the enzyme can be the tissue from which the oil or fat was extracted or it can be a contaminant from other cells including microorganisms. Besides FFA, hydrolysis of triglycerides produces glycerol. The table below shows the acid value of some common oils and bee's wax.
| Oil | Acid Value (AV)[1] |
|---|---|
| Canola | 0.071 |
| Maize | 0.223 |
| Soya | 0.60 |
| Virgin olive oil | 6.6[2] |
| Used frying oil | 31[3] |
| Bee's wax | 17-36[4] |
FFA are a source of flavors and aromas. On one side, we have short chain FFA which tend to be water soluble and volatile with characteristic smell. On the other side, we have long chain saturated and unsaturated fatty acids. The later are more prone to oxidation in their free form and their breakdown products (aldehydes, ketones, alcohols, and organic acids) provide characteristic flavors and aromas. In most cases these flavors and aromas are considered a defect in oils, fats, and foods that contain them. However, there are instances where hydrolysis of triglycerides and oxidation of FFA are key in the development of desirable flavor and aroma in foods. This is the case of aged cheeses and some processed meats.

Sunflower seed oil
The AOAC method to determine AV in fats and oils is based on a titration in ethanol using phenolphthalein as indicator. Disadvantages of this and similar methods are the use of organic solvents (volume and toxicity), the need for heating the reaction media, incomplete solubility of the oil/fat, the need to pre-neutralize the solvents, use of large amounts of sample, and the possibility of error to detect the color change of the indicator when analyzing colored samples. There are some non-titration methods designed to overcome these disadvantages.[1] However, in spite its drawbacks, the titration method is still the most used due to the fact that it does not require expensive equipment.
Acid-Base Titrations
A titration is a volumetric technique in which a solution of one reactant (the titrant) is added to a solution of a second reactant (the analyte) until the equivalence point is reached. The equivalence point is the point at which the titrant has been added in exactly the right quantity to react stoichiometrically with the analyte.
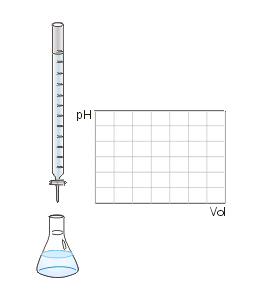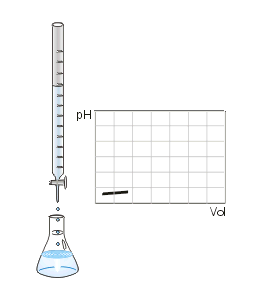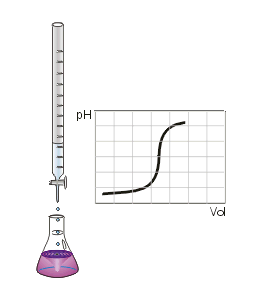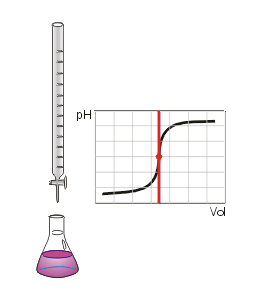
When an acid is titrated with a base, there is typically a sudden change in the pH of the solution at the equivalence point. If a few drops of indicator solution have been added, this sharp increase in pH causes an abrupt change in color, which is called the endpoint of the indicator (See the animation on the left). The actual magnitude of the jump in pH, and the pH range which it covers depend on the strength of both the acid and the base involved, and so the choice of indicator can vary from one titration to another. To learn how to choose an appropriate indicator, we need to study in some detail the variation of pH during a titration.
To simplify calculations we want to work with acid-base reactions that go to completion. For such reason, the most common cases we will encounter are:
- strong base titrated with strong acid
- strong acid titrated with strong base
- weak base titrated with strong acid
- weak acid titrated with strong base
However, we rarely titrate a weak base with a strong acid and vice versa.
Titration of a strong acid with a strong base
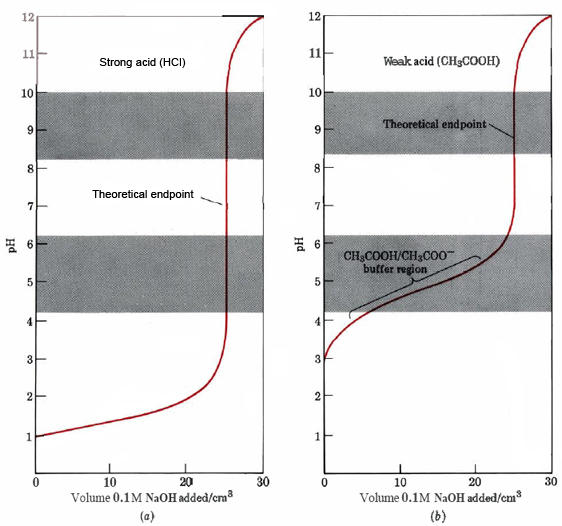
Suppose we place 25.00 cm3 of 0.10 M HCl solution in a flask and add 0.10 M NaOH from a buret. The pH of the solution in the flask varies with added NaOH, as shown in Figure 1a. The pH changes quite slowly at the start of the titration, and almost all the increase in pH takes place in the immediate vicinity of the endpoint.
The pH change during this titration is caused by the proton-transfer reaction
\(\text{H}_{3}\text{O}^{+} + \text{ OH}^{-} \rightarrow \text{ H}_{2}\text{O } + \text{ H}_{2}\text{O}\) (1) which occurs as hydroxide ions are added from the buret. Though hydronium ions are being consumed by hydroxide ions in the early stages of the titration, the hydronium-ion concentration remains in the vicinity of 10–1 or 10–2 mol dm–3. As a result, the pH remains in the range 1 to 2. As an example of this behavior let us consider the situation halfway to the endpoint, i.e., when exactly 12.50 cm3 of 0.10 M NaOH have been added to 25.00 cm3 of 0.10 M HCl in the flask. The amount of hydronium ion has been reduced at this point from an original 2.5 mmol to half this value, 1.25 mmol. At the same time the volume of solution has increased from 25 cm3 to (25 + 12.50) cm3 = 37.50 cm3. Therefore, the hydronium-ion concentration is 1.25 mmol/37.50 cm3 = 0.0333 mol dm–3, and the resultant pH is 1.48. Though the titration is half completed, this is not very different from the initial pH of 1.00.
The pH of the solution in the flask will only change drastically when we reach that point in the titration when only a minute fraction of the hydronium ions remain unconsumed, i.e., as we approach the endpoint. Only then we will have reduced the hydronium-ion concentration by several powers of 10, and consequently increased the pH by several units. When 24.95 cm3 of base have been added, we are only 0.05 cm3 (approximately one drop) short of the endpoint. At this point 24.95 cm3 × 0.10 mmol cm–3 = 2.495 mmol hydroxide ions have been added. These will have consumed 2.495 mmol hydronium ions, leaving (2.5 – 2.495) mmol = 0.005 mmol hydronium ions in a volume of 49.95 cm3. The hydronium-ion concentration will now be
\([\text{ H}_{3}\text{O}^{+}]=\frac{\text{0.005 mmol}}{\text{49.95 cm}^{3}}=\text{1.00 }\times \text{ 10}^{-4}\text{ mol dm}^{-3}\) giving a pH of 4.00. Because almost all the hydronium ions have been consumed, only a small fraction (one five-hundredth) remains and the volume of solution has nearly doubled. This reduces the hydronium-ion concentration by a factor of 10–3, and the pH increases by three units from its original value of 1.00.
When exactly 25.00 cm3 of base have been added, we have reached the theoretical equivalence point, and the flask will contain 2.5 mmol of both sodium and chloride ions in 50 cm3 of solution; i.e., the solution is 0.05 M NaCl. Furthermore its pH will be exactly 7.00, since neither the sodium ion nor the chloride ion exhibits any appreciable acid-base properties.
Immediately after this equivalence point the addition of further NaOH to the flask results in a sudden increase in the concentration of hydroxide ions, since there are now virtually no hydronium ions left to consume them. Thus even one drop (0.05 cm3) of base added to the equivalence point solution adds 0.005 mmol hydroxide ions and produces a hydroxide-ion concentration of 0.005 mmol/50.05 cm3 = 1.00 × 10–4 mol dm–3. The resultant pOH = 4.00, and the pH = 10.00. The addition of just two drops of base results in a pH jump from 4.00 to 7.00 to 10.00. This rapid rise causes the indicator to change color, so the endpoint matches the equivalence point if the indicator is chosen properly.
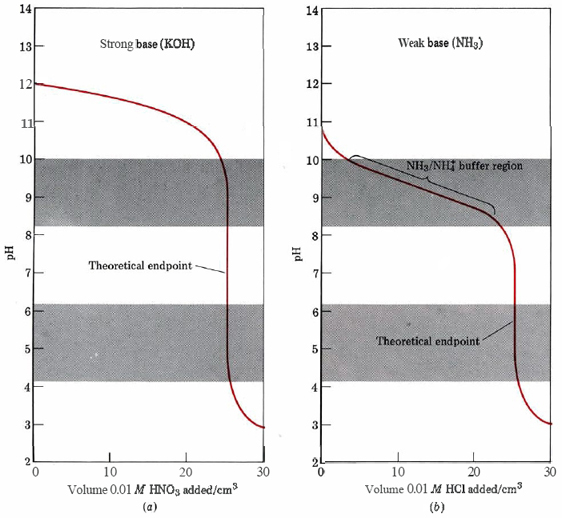
A Titration of a strong base with a strong acid can be handled in essentially the same way as the strong acid-strong base situation we have just described. Strong acids and bases are not naturally found in food, however, they are often used as food processing aids and analysis methods.
Suppose that 40.00 cm3 of 0.020 M KOH is titrated with 0.030 M HNO3. Find the pH of the solution in the flask (a) before any HNO3 is added; (b) halfway to the endpoint; (c) one drop (0.05 cm3) before the endpoint; (d) one drop after the endpoint.
Solution
a) Since KOH is a strong base, [OH–] = 0.020 = 2 x 10–2. Thus
\(\text{pOH}=\text{1.7}\,\) and \(\text{pH}=\text{14} - \text{2} = \text{12.3}\,\)
\(\begin{align} n_{\text{OH}^{-}}&=V_{\text{NaOH}}\times c_{\text{NaOH}}\\ \text{ }&=\text{40.00 cm}^{3}\times \frac{\text{0.020 mmol}}{\text{1 cm}^{3}}=\text{0.8 mmol} \end{align}\) so the amount remaining is 0.4 mmol OH–. It must have required 0.4 mmol HNO3 to consume the other 0.4 mmol OH–, and so the volume of HNO3 added is
\(\begin{align} V_{\text{HNO}_{3}}&=\frac{n_{\text{HNO}_{3}}}{c_{\text{HNO}_{3}}}\\ \text{ }&=\frac{\text{0.4 mmol}}{\text{0.030 mmol cm}^{-3}}=\text{13.33 cm}^{3} \end{align}\) The total volume of solution at this point is thus (13.33 + 40.00) cm3 = 53.33 cm3, and
\(\begin{align}\text{ } [\text{ OH}^{-}]& = \frac{\text{0.4 mmol}}{\text{53.33 cm}^{3}}\\ \text{ }&=\text{7.50 }\times \text{ 10}^{-3}\text{ mmol cm}^{-3}=\text{7.50 }\times \text{ 10}^{-3}\text{ mol dm}^{-3} \end{align}\)
\(\text{pOH} = -\text{log }(\text{7.50} \times \text{10}^{-3})= \text{2.12}\) and
\(\text{pH}=\text{14}-\text{2.12}=\text{11.88}\,\) c) If the total volume of of HNO3 required to react with all the OH- in solution is 26.66 cm3, when 26.61 cm3 of HNO3 solution have been added, the amount of H3O+ added is
\(\begin{align} n_{\text{H}_{3}\text{O}^{+}}=\text{26.61 cm}^{3}\times \frac{\text{0.030 mmol}}{\text{1 cm}^{3}}=\text{0.798 mmol} \end{align}\) This would consume an equal amount of OH–, and so the amount of OH– remaining is (0.8 – 0.798) mmol = 0.002 mmol. Thus
\(\begin{align} \text{ }[\text{ OH}^{-}]&=\frac{\text{0.002 mmol}}{\text{(40 + 26.61) cm}^{3}}\\ \text{ }&=\text{3.00 }\times \text{ 10}^{-5}\text{ mmol cm}^{-3}=\text{3.00 }\times \text{ 10}^{-5}\text{ mol dm}^{-3} \end{align}\)
\(\text{pOH} = \text{4.52}\,\) and \(\text {pH}= \text{9.48}\,\) d) An excess of 0.05 cm3 of acid will add
\(\begin{align} n_{\text{H}_{3}\text{O}^{+}}=\text{0.05 cm}^{3}\times \frac{\text{0.030 mmol}}{\text{1 cm}^{3}}=\text{1.5 }\times \text{ 10}^{-3}\text{ mmol} \end{align}\)
of H3O+ to a neutral solution whose volume is (40.00 + 26.71)cm3 = 66.71 cm3.Thus
\([\text{ H}_{3}\text{O}^{+}]=\frac{\text{1.5 }\times \text{ 10}^{-3}\text{ mmol}}{\text{66.71 cm}^{3}}=\text{2.25 }\times \text{ 10}^{-5}\text{ mol dm}^{-3}\)\(\text {pH}= \text{4.64}\,\)
Titration of a weak acid with a strong base
When 25.00 cm3 of 0.10M CH3COOH is titrated with 0.10M NaOH, for instance, there is a very much smaller change in pH at the equivalence point, as shown in Figure 1b, and the choice of indicators is correspondingly narrowed. The behavior of the pH in this case is very different from that of the titration of HCl with NaOH, because the acid-base reaction is different. When CH3COOH is titrated with NaOH, the OH– ions consume CH3COOH molecules according to the equation
\(\text{OH}^{-} + \text{ CH}_{3}\text{COOH } \rightarrow \text{ H}_{2}\text{O } + \text{ CH}_{3}\text{COO}^{-}\) (2)
As a result, the solution in the titration flask soon becomes a buffer mixture with appreciable concentrations of the CH3COO– ion as well as its conjugate acid. The [H3O+] and the pH are then controlled by the ratio of acid to conjugate base (equations 2 and 3 in the section on buffer solutions). When we are halfway to the endpoint, for example, [CH3COOH] will be essentially the same as [CH3COO–], and
\(\begin{align} \text{ }[\text{ H}_{3}\text{O}^{\text{+}}]&=K_{a}\times \frac{[\text{ CH}_{3}\text{COOH }]}{[\text{ CH}_{3}\text{COO}^{-}]}\\ \text{ }&\approx \text{ }K_{a}=\text{1.8 }\times \text{ 10}^{-5}\text{ mol dm}^{-3}\end{align}\)
while the pH will be given by the Henderson-Hasselbalch equation as
\(\begin{align}\text{pH}&=\text{p}K_{a}\text{ + log }\frac{[\text{ CH}_{3}\text{COOH }]}{[\text{ CH}_{3}\text{COO}^{-}]}\\ \text{ }&\approx \text{ p}K_{a}=\text{4.74}\end{align}\)
Comparing this to the pH of 1.78 calculated above for the halfway stage in the titration of HCl, we find a difference of roughly three pH units. The effect of the buffering action of the CH3COOH/ CH3COO– conjugate pair is thus to keep the pH some three units higher than before and hence to cut the jump in pH at the endpoint by approximately this amount.
Exactly at the equivalence point we no longer have a buffer mixture but a 0.05-M solution of sodium acetate. This solution is slightly basic, and its pH of 8.72 can be calculated from equation 4 on the section covering the pH of weak base solutions. Beyond this equivalence point, the story is much the same as in the strong-acid case. Addition of even a drop (0.05cm3) of excess base raises the OH– concentration to 10–4 mol dm–3 and the pH to 10. Of the three indicators which could be used in the titration of HCl, only one is useful for acetic acid. This is phenolphthalein, which changes color in the pH range 8.3 to 10.0. This endpoint lies within the pH jump from 7 to 10 which occurs ± 0.05 cm3 (one drop) from the endpoint. Both the other two indicators would give a color change before the true equivalence point. As shown in Figure 1b, the color of methyl red would start changing after only about 4 cm3 of base had been added!
The titration of a weak base with a strong acid also involves a buffer solution and consequently requires a more careful choice of indicator.
The pH variation during titrations of strong and weak bases with a strong acid are shown in Figure 2. In the case of the titration of 0.010 M NH3 with 0.010 M HCl, methyl red, but not phenolphthalein, would be a suitable indicator. In general the best indicator for a given titration is the one whose pKa most nearly matches the pH calculated at the theoretical endpoint.
Ten grams of olive oil are dispersed in 50 cm3 ethanol for a final volume of 60.86 cm3. The mixture is titrated with 50 cm3 KOH 0.1 M. a) What is the AV of this sample of olive oil? Assuming that the only free fatty acid present in the sample is oleic acid and that we are working with an aqueous solution at all times, what is the pH of the mixture b) before any KOH is added?, when c) 10 cm3, d) 25 cm3, e) 35 cm3 e) an excess of 1.5cm3 KOH 0.1 M have been added?
Note: Oleic acid (c-9-octadecenoic) pKa=9.85[5]
Solution
a) If 50 cm3 of 0.1 M KOH were used to neutralize the sample, the number of moles of KOH is
\(\begin{align} n_{\text{KOH}}&=V_{\text{KOH}}\times c_{\text{KOH}}\\ \text{ }&=\text{50.00 cm}^{3}\times \frac{\text{0.1 mmol}}{\text{1 cm}^{3}}=\text{5.0 mmol} \end{align}\) The molar mass of KOH is 56.10 g/mol and the mass of KOH employed in mg is \(\begin{align} m_{\text{KOH}}&=n_{\text{KOH}}\times M_{\text{KOH}}\\ \text{ }&=\text{5.0 mmol}\times \frac{\text{56.10 mg}}{\text{mmol}}=\text{280.5 mg} \end{align}\)this amount of KOH was used to neutralize 10 g of olive oil. The acid value is the then
\(\begin{align} \text{AV}&=\frac {\text{mg}_{\text{ KOH}}}{\text{g}_{\text{ sample}}}\\ \text{ }&=\frac {\text{280.5 mg}_{\text{ KOH}}}{\text{10 g}_{\text{ sample}}}=\text{28.05} \end{align}\) This AV is considerable higher than the one shown in the table above. What does this tell you about the oil?This oil has probably been heated (cooking/frying), it is old, or it has been stored under conditions favoring lipase activity. In the case of refined oils, a high AV indicates inappropriate or incomplete refining procedures.
b) From the number of moles of KOH employed to neutralize the oil we can conclude that there were 5.0 mmol of oleic acid in the sample and the ethanolic dispersion. Given that the volume of the dispersion was 60.83 cm3 the concentration of oleic acid is then
\(\begin{align} c_{\text{oleic}}&=\frac {n_{\text{oleic}}}Callstack:
at (Bookshelves/General_Chemistry/ChemPRIME_(Moore_et_al.)/14:_Ionic_Equilibria_in_Aqueous_Solutions/14.10:_Titration_Curves/14.10.01:_Foods-_Acid_Value_and_the_Quality_of_Fats_and_Oils), /content/body/div[3]/section/div/div/span[1], line 1, column 1
\(\begin{align}\text{ }[\text{ H}_{\text{3}}\text{O}^{\text{+}}\text{ }]\text{ }&=\sqrt{K_{a}c_{a}} \\ \text{ }&=\sqrt{(\text{1.41}\times \text{ 10}^{-10}\text{ mol dm}^{-3})(\text{ 0.082}\text{ mol dm}^{-3})} \\ \text{ }&=\sqrt{\text{1.16}\times \text{ 10}^{-11}\text{ mol}^{\text{2}}\text{ dm}^{-6}}\\ \text{ }[\text{ H}_{\text{3}}\text{O}^{\text{+}}\text{ }]\text{ }&=\text{3.4}\times \text{ 10}^{-\text{6}}\text{ mol dm}^{-\text{3}} \\ \text{pH}&=-\text{log (3.4 }\times \text{ 10}^{-6}\text{)}=\text{5.47} \\ \end{align}\)
c) When 10 cm3 of KOH solution had been added, the volume of the dispersion is 60.83 + 10 = 70.83 cm3 and the corresponding number of moles of OH- is \(\begin{align} n_{\text{OH}^{-}}&=V_{\text{OH}^{-}}\times c_{\text{OH}^{-}}\\ \text{ }&=\text{10.00 cm}^{3}\times \frac{\text{0.1 mmol}}{\text{1 cm}^{3}}=\text{1.0 mmol} \end{align}\) This means that 1.0 mmol of oleic acid have reacted and produced 1.0 mmol of oleate, its conjugate base. At this point, the number of moles of oleic acid and oleate are \(\begin{align}n_{\text{oleic}}&= \text{5.0 mmol} - \text{1.0 mmol} = \text{4.0 } \text{mmol oleic acid}\\ n_{\text{oleate}}&= \text{1.0 mmol oleate}\,\end{align}\) and their concentrations \(\begin{align} c_{\text{oleic}}&=\frac {n_{\text{oleic}}}Callstack:
at (Bookshelves/General_Chemistry/ChemPRIME_(Moore_et_al.)/14:_Ionic_Equilibria_in_Aqueous_Solutions/14.10:_Titration_Curves/14.10.01:_Foods-_Acid_Value_and_the_Quality_of_Fats_and_Oils), /content/body/div[3]/section/div/div/span[2], line 1, column 1
Callstack:
at (Bookshelves/General_Chemistry/ChemPRIME_(Moore_et_al.)/14:_Ionic_Equilibria_in_Aqueous_Solutions/14.10:_Titration_Curves/14.10.01:_Foods-_Acid_Value_and_the_Quality_of_Fats_and_Oils), /content/body/div[3]/section/div/div/span[3], line 1, column 1
f) If an excess of 1.5 cm3 are added to the dispersion, its final volume is 112.33 cm3. Since all the oleic acid has been converted into oleate, there are no more protons to react with the OH- ions and it will remain in solution.
The number of moles of OH- ions is
\(\begin{align} n_{\text{OH}^{-}}&=V_{\text{OH}^{-}}\times c_{\text{OH}^{-}}\\ \text{ }&=\text{1.5 cm}^{3}\times \frac{\text{0.1 mmol}}{\text{1 cm}^{3}}=\text{0.15 mmol} \end{align}\) for a concentration of Since the OH- is the strongest base in solution, it will govern the pH of the reaction mixture. The concentration of OH- generated by oleate is negligible, so we calculate the pH of the dispersion as\(\begin{align}\text{pOH}&= -\text{log }[\text{OH}^{-}]\\ \text{ }&=-\text{log }(\text{1.33} \times \text{10}^{-3})= \text{2.87}\end{align}\)
and
\(\text{pH}=\text{14}-\text{2.82}=\text{11.18}\,\) Notice the assumptions we made to calculate pH at different stages of this titration. Initially, the oil is dispersed in ethanol, the dissociation constants of acids change depending on the medium and strictly speaking it is probably incorrect to talk about pH in this conditions. The method is also based on the assumption that protons are in the interface ethanol-water and readily react with aqueous NaOH. These are some of the limitations of the method and the reason for the need of a titration instead of direct measurement of pH on the sample.References
- Kardash, E. and Tur’yan, Y. I. 2005. Acid Value Determination in Vegetable Oils by Indirect Titration in Aqueous-alcohol Media. Croat. Chem. Acta 78:1:99-103.
- www.unctad.org/infocomm/angla...c/Cxs_033e.pdf
- Cao, F., Chen, Y., Zhai, F., Li, J., Wang, J., Wang, X., Wang, S., and Zhu, W. 2008. Biodiesel Production From High Acid Value Waste Frying Oil Catalyzed by Superacid Heteropolyacid. Biotech. Bioeng. 101:1:93-100.
- Food Lipids. Akoh, C. C., and Min, D.B. 3rd ed.
- Kanicky, J.R. and Shah, D. O. 2002.Effect of degree, type, and position of unsaturation on the pKa of long-chain fatty acids. J. Colloid Interface Sci. 256:1:201-207
Contributors
Ed Vitz (Kutztown University), John W. Moore (UW-Madison), Justin Shorb (Hope College), Xavier Prat-Resina (University of Minnesota Rochester), Tim Wendorff, and Adam Hahn.