11.4: Hydration of Ions

We have already stated several times that solubility in water is a characteristic property of many ionic compounds, and Table 1 from Precipitation Reactions provides further confirmation of this fact. We have also presented experimental evidence that ions in solution are nearly independent of one another. This raises an important question, though, because we have also stated that attractive forces between oppositely charged ions in a crystal lattice are large. The high melting and boiling points of ionic compounds provide confirmation of the expected difficulty of separating oppositely charged ions. How, then, can ionic compounds dissolve at room temperature? Surely far more energy would be required for an ion to escape from the crystal lattice into solution than even the most energetic ions would possess.

Figure \(\PageIndex{1}\): The hydration of (a) a positive ion; (b) a negative ion. When ions are dissolved in water, they attract and hold several water dipoles around them shown in the circular area in the circular area in the center of each part of the diagram.

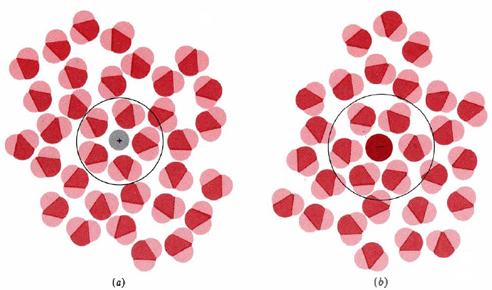
The resolution of this apparent paradox lies in the interactions between ions and the molecules of water or other polar solvents. The negative (oxygen) side of a dipolar water molecule attracts and is attracted by any positive ion in solution. Because of this ion-dipole force, water molecules cluster around positive ions, as shown in Figure \(\PageIndex{1}\) a. Similarly, the positive (hydrogen) ends of water molecules are attracted to negative ions. This process, in which either a positive or a negative ion attracts water molecules to its immediate vicinity, is called hydration.

When water molecules move closer to ions under the influence of their mutual attraction, there is a net lowering of the potential energy of the microscopic particles. This counteracts the increase in potential energy which occurs when ions are separated from a crystal lattice against their attractions for other ions.

Thus the process of dissolving an ionic solid may be divided into the two hypothetical steps shown in Figure \(\PageIndex{2}\). First, the crystalline salt is separated into gaseous ions. The heat energy absorbed when the ions are separated this way is called the lattice enthalpy (or sometimes the lattice energy). Next, the separate ions are placed in solution; that is, water molecules are permitted to surround the ions. The enthalpy change for this process is called the hydration enthalpy.

Figure \(\PageIndex{2}\): Enthalpy changes and solution. There is usually very little energy or enthalpy change when ionic solids like NaCl dissolve in H₂O since the energy needed to separate the ions from each other is not very different from the energy liberated when the ions become hydrated by attracting H₂O dipoles around them.

Since there is a lowering of the potential energy of the ions and water molecules, heat energy is given off and hydration enthalpies are invariably negative. The heat energy absorbed when a solute dissolves (at a pressure of 1.00 atm) is called the enthalpy of solution. It can be calculated using Hess' law, provided the lattice enthalpy and hydration enthalpy are known.

Example \(\PageIndex{1}\): Enthalpy

Using data given in Figure \(\PageIndex{2}\), calculate the enthalpy of solution for NaCl(s).

Solution

According to the figure, the lattice enthalpy is 773 kJ mol^–1. The hydration enthalpy is – 769 kJ mol^–1. Thus we can write the thermo-chemical equations

\(\text{NaCl}(s) \rightarrow \text{Na}^{+}(g) + \text{Cl}^{-}(g) \) \(\triangle H_f = 773 \frac{kJ}{mol}\)

\(\underline{\text{Na}^{+}(g) + \text{Cl}^{-}(g) \rightarrow \text{Na}^{+}(aq) + \text{Cl}^-(aq)}\) \(\triangle H_h = -769 \frac{kJ}{mol}\)

\(\text{NaCl}(s) \rightarrow \text{Na}^{+}(aq) + \text{Cl}^{-}(aq)\) \(\triangle H_s=\triangle H_f + \triangle H_h\)

\(\triangle H_s = (773-769)\frac{kJ}{mol} = +4\frac{kJ}{mol} \)

When NaCl(s) dissolves, 773 kJ is required to pull apart a mole of Na⁺ ions from a mole of Cl^– ions, but almost all of this requirement is provided by the 769 kJ released when the mole of Na⁺ and the mole of Cl^– becomes surrounded by water dipoles. Only 4 kJ of heat energy is absorbed from the surroundings when a mole of NaCl(s) dissolves. You can verify the small size of this enthalpy change by putting a few grains of salt on your moist tongue. The quantity of heat energy absorbed as the salt dissolves is so small that you will feel no cooling, even though your tongue is quite a sensitive indicator of temperature changes.

Few molecules are both small enough and polar to cluster around positive and negative ions in solution as water does. Consequently water is one of the few liquids which readily dissolves many ionic solids. Hydration of Na⁺, Cl^– and other ions in aqueous solution prevents them from attracting each other into a crystal lattice and precipitating.