11.2: Ions in Solution (Electrolytes)
- Page ID
- 49484
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In Binary Ionic Compounds and Their Properties we point out that when an ionic compound dissolves in water, the positive and negative ions originally present in the crystal lattice persist in solution. Their ability to move nearly independently through the solution permits them to carry positive or negative electrical charges from one place to another. Hence the solution conducts an electrical current.
Electrolytes
Substances whose solutions conduct electricity are called electrolytes. All soluble ionic compounds are strong electrolytes. They conduct very well because they provide a plentiful supply of ions in solution. Some polar covalent compounds are also strong electrolytes. Common examples are HCl, HBr, HI and H2SO4, all of which react with H2O to form large concentrations of ions. A solution of HCl, for example, conducts even better than one of NaCl having the same concentration.
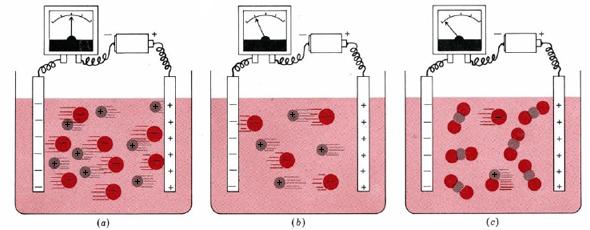
The effect of the concentration of ions on the electrical current flowing through a solution is illustrated in Figure \(\PageIndex{1}\). Part a of the figure shows what happens when a battery is connected through an electrical meter to two inert metal strips (electrodes) dipping in ethanol. Each cubic decimeter of such a solution contains 0.10 mol NaCl (that is, 0.10 mol Na+ and 0.10 mol Cl–). An electrical current is carried through the solution both by the Na+ ions moving toward the negative electrode and by the Cl- ions which are attracted toward the positive electrode. The dial on the meter indicates the quantity of current.
Figure 1b shows that if we replace the 0.10-M NaCl solution with a 0.05-M NaCl solution, the meter reading falls to about one-half its former value. Halving the concentration of NaCl halves the number of ions between the electrodes, and half as many ions can only carry half as much electrical charge. Therefore the current is half as great. Because it responds in such a direct way to the concentration of ions, conductivity of electrical current is a useful tool in the study of solutions.
Conductivity measurements reveal that most covalent compounds, if they dissolve in water at all, retain their original molecular structures. Neutral molecules cannot carry electrical charges through the solution, and so no current flows. A substance whose aqueous solution conducts no better than water itself is called a nonelectrolyte. Some examples are oxygen, O2, ethanol, C2H5OH, and sugar, C12H22O11.

Some covalent substances behave as weak electrolytes—their solutions allow only a small current flow, but it is greater than that of the pure solvent. An example is mercury(II) chloride (seen in the Figure above). For a 100-M HgCl2 solution the meter reading shows only about 0.2 percent as much current as for 0.10 M NaCl. A crystal of HgCl2 consists of discrete molecules, like those shown for HgBr2 in Figure \(\PageIndex{2}\). When the solid dissolves, most of these molecules remain intact, but a few dissociate into ions according to the equation
\[ \underbrace{HgCl_2}_{99.8\%} \rightleftharpoons \underbrace{HgCl^+}_{0.2\%} + Cl^- \nonumber \]
(The double arrows indicate that the ionization proceeds only to a limited extent and an equilibrium state is attained.) Since only 0.2 percent of the HgCl2 forms ions, the 0.10 M solution can conduct only about 0.2 percent as much current as 0.10 M NaCl.
Conductivity measurements can tell us more than whether a substance is a strong, a weak, or a nonelectrolyte. Consider, for instance, the data in Table \(\PageIndex{1}\) which shows the electrical current conducted through various aqueous solutions under identical conditions. At the rather low concentration of 0.001 M, the strong electrolyte solutions conduct between 2500 and 10 000 times as much current as pure H2O and about 10 times as much as the weak electrolytes HC2H3O2 (acetic acid) and NH3 (ammonia).
Closer examination of the data for strong electrolytes reveals that some compounds which contain H or OH groups [such as HCl or Ba(OH)2] conduct unusually well. If these compounds are excluded, we find that 1:1 electrolytes (compounds which consist of equal numbers of +1 ions and –1 ions) usually conduct about half as much current as 2:2 electrolytes (+2 and -2 ions), 1:2 electrolytes (+1 and -2 ions), or 2:1 electrolytes (+2 and -1 ions).
| Substance | Current /mA | Substance | Current /mA |
|---|---|---|---|
| Pure Water | 1:2 Electrolytes | ||
| H2O | 3.69 x 10-4 | Na2SO4 | 2.134 |
| Weak Electrolytes | Na2CO3 | 2.24 | |
| HC2H3O2 | 0.41 | K2CO3 | 2.660 |
| NH3 | 0.28 | 2:1 Electrolytes | |
| 1:1 Electrolytes | MgCl2 | 2.128 | |
| NaCl | 1.065 | CaCl2 | 2.239 |
| NaI | 1.069 | SrCl2 | 2.290 |
| KCl | 1.273 | BaCl2 | 2.312 |
| KI | 1,282 | Ba(OH)2 | 4.14 |
| AgNO3 | 1.131 | 2:2 Electrolytes | |
| HCl | 3.77 | MgSO4 | 2.00 |
| HNO3 | 3.75 | CaSO4 | 2.086 |
| NaOH | 2.08 | CuSO4 | 1.97 |
| KOH | 2.34 | ZnSO4 | 1.97 |
* All measurements refer to a cell in which the distance between the electrodes is 1.0 mm and the area of each electrode is 1.0 cm². A potential difference of 1.0 V is applied to produce the tabulated currents.
There is a simple reason for this behavior. Under similar conditions, most ions move through water at comparable speeds. This means that ions like Mg2+ or SO42–, which are doubly charged, will carry twice as much current through the solution as will singly charged ions like Na+ or Cl–. Consequently, a 0.001 M solution of a 2:2 electrolyte like MgSO4 will conduct about twice as well as a 0.001 M solution of a 1:1 electrolyte like NaCl.
A similar argument applies to solutions of 1:2 and 2:1 electrolytes. A solution like 0.001 M Na2SO4 conducts about twice as well as 0.001 M NaCl partly because there are twice as many Na– ions available to move when a battery is connected, but also because SO42– ions carry twice as much charge as Cl– ions when moving at the same speed. These differences in conductivity between different types of strong electrolytes can sometimes be very useful in deciding what ions are actually present in a given electrolyte solution as the following example makes clear.
A second, slightly more subtle, conclusion can be drawn from the data in Table \(\PageIndex{1}\). When an electrolyte dissolves, each type of ion makes an independent contribution to the current the solution conducts. This can be seen by comparing NaCl with KCl, and NaI with KI. In each case the compound containing K+ conducts about 0.2 mA more than the one containing Na+. If we apply this observation to Na2CO3 and K2CO3, each of which produces twice as many Na+ or K+ ions in solution, we find that the difference in current is also twice as great—about 0.4 mA.
Thus conductivity measurements confirm our statement that each ion exhibits its own characteristic properties in aqueous solutions, independent of the presence of other ions. One such characteristic property is the quantity of electrical current that a given concentration of a certain type of ion can carry.
At 18°C a 0.001-M aqueous solution of potassium hydrogen carbonate, KHCO3, conducts a current of 1.10 mA in a cell of the same design as that used to obtain the data in Table 11.1. What ions are present in solution?
Solution
Referring to Table 6.2 which lists possible polyatomic ions, we can arrive at three possibilities for the ions from which KHCO3 is made:
- K+ and H+ and C4+ and three O2–
- K+ and H+ and CO32–
- K+ and HCO3–
Since the current conducted by the solution falls in the range of 1.0 to 1.3 mA characteristic of 1:1 electrolytes, possibility c is the only reasonable choice.


