8.4: London Forces
- Page ID
- 49421
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Dipole forces explain how polar molecules can attract each other, but it is a bit harder to account for the forces of attraction which exist between completely nonpolar molecules. Even the noble gases, whose atoms do not form chemical bonds with each other, can be condensed to liquids at sufficiently low temperatures. This indicates that the atoms attract each other, though only feebly. An explanation of these attractive forces was first given in 1930 by the Austrian physicist Fritz London (1900 to 1954). According to his theory, when two molecules approach each other very closely, the motion of the electrons in one of the molecules interferes with the motion of the electrons in the other, and the net result is an attractive force. In order to understand London’s ideas better, let us start by considering the hypothetical situation shown in Figure \(\PageIndex{1}\). When a dipole approaches a helium atom, the electron cloud of the helium atom is attracted toward the positive end of the dipole.
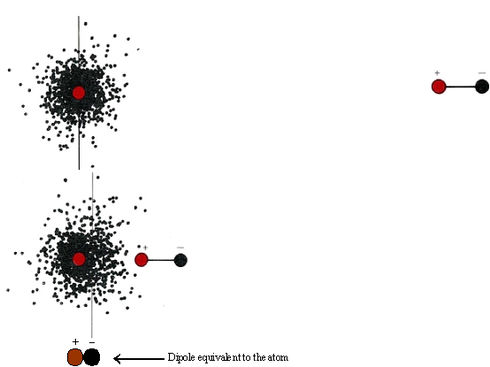
The helium atom becomes polarized and behaves electrically as though it were a second dipole, with its negative side pointed toward the positive side of the first dipole. As we have already seen, two dipoles oriented in this fashion attract each other.
If instead of a dipole, we now bring up another helium atom, a similar effect occurs. The electrons moving about the nucleus in this second atom will often both be found momentarily on one side of the nucleus or both on the other side. At any given instant, therefore, the approaching helium atom is likely to be slightly polar. It can then behave like the dipole used in the above figure, inducing a dipole in the first atom, and attraction will result. Thus, as the electrons in one atom move around it, they will tend to synchronize to some extent with the motion of the electrons in the other atom. Overall there will be a force of attraction between the two helium atoms.
An argument similar to that just presented can be applied to pairs of atoms of the other noble gases as well. Indeed, it explains why there must be forces of attraction, albeit quite small, between two molecules of any kind. Forces caused by the mutual instantaneous polarization of two molecules are called London forces, or sometimes dispersion forces. When referring to intermolecular forces in general, to either London or dipole forces or both, the term van der Waals forces is generally used. Johannes van der Waals (1837 to 1923) was a Dutch scientist who first realized that neutral molecules must attract each other, even though he was unable to explain these attractions himself.
In general, when we compare substances whose molecules have similar electronic structures, it is always the larger molecules which correspond to the stronger London forces. This rule is illustrated by the physical properties shown in the following table for the noble gases and the halogens. Both melting points and boiling points increase in the order He < Ne < Ar < Kr < Xe and F2 < Cl2 < Br2 < I2. This corresponds with the order of increasing van der Waals radius, showing that in each case the larger molecules are more strongly attracted to each other.
| Substance | van der Waals Radius* / pm | Melting Point (in °C) | Boiling Point (in °C) |
|---|---|---|---|
| He | 93 | † | -269 |
| Ne | 112 | -248 | -246 |
| Ar | 154 | -189 | -186 |
| Kr | 169 | -157 | -153 |
| Xe | 190 | -112 | -108 |
| F2 | 135 | -220 | -188 |
| Cl2 | 180 | -101 | -34 |
| Br2 | 195 | -47 | 58 |
| I2 | 215 | 114 | 183 |
* From figure of atomic radii. Note that the halogen molecules are not spherical. Nevertheless the van Waals radius of the halogen atoms is in proportion to molecular size.
† Only forms a solid at very high pressures.
This dependence on the size of the molecule is readily explained by London’s theory. In larger molecules, the valence electrons are on the whole farther from the nuclei. The electron cloud is more diffuse, less tightly held, and hence more easily polarizable than for smaller molecules. The ionization energy for Xe is 1170 kJ mol–1, for example, much less than for Ne (2080 kJ mol–1 as seen in the table of ionization energies). This indicates that the outermost octet in Xe is much less tightly held than in Ne. Thus when two Xe atoms approach each other closely, the motion of the electrons in the one atom can synchronize with the motion in the other more effectively than in the case of two Ne atoms.
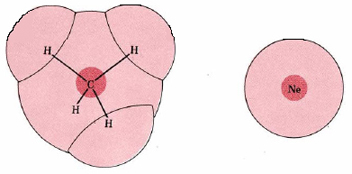
The magnitude of London forces is often said to depend on the molar mass of the molecules involved; if we compare molecules of similar electronic structure, the larger molecules are usually the heavier ones. But this is a coincidence rather than a cause-and-effect relationship, and is not always true. If we compare methane, CH4 (M = 16 g mol–1) with Ne (M = 20.2 g mol–1), for example, we find that the lighter molecule has the stronger London forces. Both molecules contain 10 electrons, of which 8 are in valence shell. In an Ne atom, the electrons are tightly held by a single nucleus of charge +10, while in CH4, this same total positive charge is spread out over one C nucleus of charge +6 and four H nuclei of charge +1. As can be seen from Figure 2, the electrons in CH4 occupy a much larger electron cloud and are not so tightly constrained as in Ne. They are thus easier to polarize, and the London forces between two CH4 molecules are expected to be larger than between two Ne molecules. In agreement with this we find a much higher boiling point for CH4 (–162°C) than for Ne (–246°C).
Decide which substance in each of the following pairs will have the higher boiling point:
- SiH4 vs. SnH4...
- CF4 vs. CCl4
- Kr vs. HBr
- C2H6 vs.F2
Solution
- Both SiH4 and SnH4 correspond to the same Lewis diagram. In SnH4 though, the valence octet is in the n = 5 shell, as opposed to the n = 3 shell for SiH4. SnH4 is the larger molecule and should have the higher boiling point.
- Again the two molecules have similar Lewis diagrams. Since Cl is larger than F, we conclude that electrons in CCl4 are more easily polarized, and the boiling point will be higher for this compound.
- Both Kr and HBr have the same number of electrons. HBr, however, is polar and thus has the higher boiling point.
- Both molecules have the same total number of electrons, namely, 18, but in C2H6 the electron cloud is distributed around eight nuclei rather than two. This larger cloud is more easily polarized so that we can expect stronger London forces. C2H6, F2 will thus have the higher boiling point.
Note that it is not always possible to decide which of two substances has the higher boiling point even though their electronic structures are very similar. A case in point is the pair of substances HCl and HI. We can expect HCl to be more polar than HI so that the dipole forces between HCl molecules should be greater than for HI molecules. The London forces, however, will be the other way around since HI is so much larger in size than HCl. It happens that the effect of the London forces is larger—HI is found to have a higher boiling point (–38°C) than HCl (–88°C).


