6.19: Atomic Sizes

 The sizes of atoms and ions are important in determining the properties of both covalent and ionic compounds. You should already have some appreciation of the factors which govern atomic sizes from the color-coded dot-density diagrams of Hydrogen, Helium, and Lithium and of Beryllium, Boron and Carbon. From the leftmost diagram below, one can see that Hydrogen seems to have a larger atomic radius than Helium, but not larger than Lithium (although it's "radius" is quite spread out). On the right side, one can see that the atomic radius steadily decreases as you go down the line. Note the relative locations of these elements on the periodic table and predict what the trend might be.

Figure \(\PageIndex{1}\) The figures above show the electron density of different elements. On the left from top to bottom are Hydrogen, Helium, and Lithium. On the right from top to bottom are Beryllium, Boron, and Carbon.

Hydrogen has a larger circular area concentrated with dots when compared to helium. Lithium has a 2 s orbital which translates to a significantly larger circular area in which the electrons are dispersed. The electron density diagram of Hydrogen and helium are superimposed on the diagram for lithium to better highlight the difference in sizes.

The circular area for beryllium is the largest since the electrons are more spread apart. The electron density for boron shows a circular area concentrated with dots but there are also two lobed area symmetrical about the vertical axis. This lobed region is also highly concentrated with dots. The electron density diagram for Carbon has four lobed shape region pointing to each side of the axis that are highly concentrated with dots. It also has the circular area in the center which is highly concentrated with dots. The area covered by electrons in boron is larger than carbon but still smaller than beryllium.

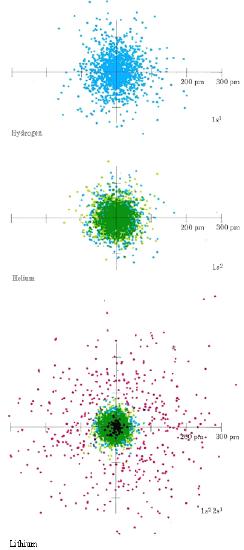
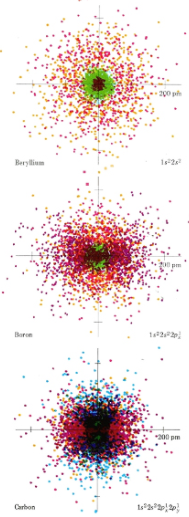
By far the largest atom illustrated in these color plates is Li. Because Li has an electron in the n = 2 shell, it is larger than H or He whose 1s electron clouds are much closer to the nucleus. Li is also larger than Be, B, or C. In the latter atoms, the 2s and 2p electron clouds are attracted by a greater nuclear charge and hence are held closer to the center of the atom than the 2s cloud in Li. Thus two important rules may be applied to the prediction of atomic sizes.

1 As one moves from top to bottom of the periodic table, the principal quantum number n increases and electrons occupy orbitals whose electron clouds are successively farther from the nucleus. The atomic radii increase.

2 As one moves from left to right across a horizontal period, then n value of the outermost electron clouds remains the same, but the nuclear charge increases steadily. The increased nuclear attraction contracts the electron cloud, and hence the atomic size decreases.

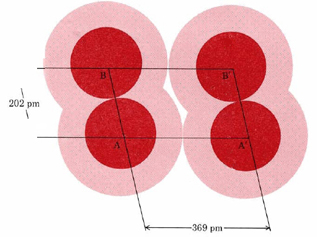
It is difficult to measure the size of an atom very exactly. As the dot-density diagrams show, an atom is not like a billiard ball which has a definite radius. Instead of stopping suddenly, an electron cloud gradually fades out so that one cannot point to a definite radius at which it ends. One way out of this difficulty is to find out how closely atoms are packed together in a crystal lattice. Figure \(\PageIndex{2}\) illustrates part of a crystal of solid Cl₂ at a very low temperature. The distance AA′ has the value of 369 pm. Since this represents the distance between adjacent atoms in different Cl₂ molecules, we can take it as the distance at which different Cl atoms just “touch.” Half this distance, 184 pm, is called the van der Waals radius of Cl. The van der Waals radius gives an approximate idea of how closely atoms in different molecules can approach each other.

Figure \(\PageIndex{2}\) The relationship between van der Waals radii and covalent radii for Cl₂(s). In solid chlorine the molecules pack together so that the shortest distance between chlorine nuclei in different molecules (AA′ or BB′) or is 369 pm. The van der Waals radius of chlorine is defined as half that distance or 184 pm. The covalent radius of chlorine is half the distance (one-half AB or A′B′) between two chlorine nuclei in the same molecule. This is smaller than the van der Waals radius because of the covalent bond in each Cl₂ molecule.

Commonly accepted values of the van der Waals radii for the representative elements are shown in the Figure \(\PageIndex{3}\). Note how these radii decrease across and increase down the periodic table.

Figure \(\PageIndex{3}\) Sizes of atoms of the representative elements as a function of their position in the periodic table. Outer (lightly shaded) circles indicate van der Waals radii, while inner (darkly shaded) circles represent covalent radii. Colored numbers are van der Waals radii, and black numbers are covalent radii, both expressed in picometers.

Also given are values for the covalent radius of each atom. Returning to the figure of Cl₂ (Figure \(\PageIndex{2}\), we see that the distance AB between two Cl atoms in the same molecule (i.e., the Cl—Cl bond length) has a value of 202 pm. The covalent radius is one-half of this bond length, or 101 pm. Covalent radii are approximately additive and enable us to predict rough values for the internuclear distances in a variety of molecules. For example, if we add the covalent radius of C (77 pm) to that of O (66 pm), we obtain an estimate for the length of the C―O bond, namely, 143 pm. This is in exact agreement with the measured value in ethyl alcohol and dimethyl ether seen previously.