6.11: Physical Properties
- Page ID
- 49355
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
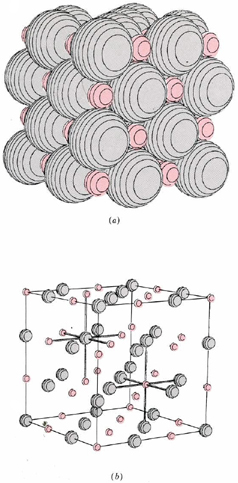
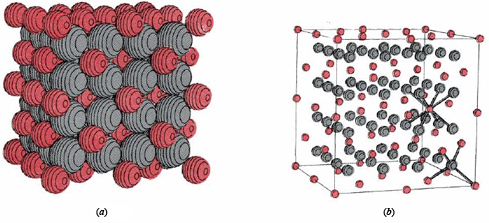
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Binary ionic compounds have many macroscopic properties in common, some of which are easy to explain in terms of the microscopic picture just presented. Because each ion in a crystal lattice, like those shown for lithium hydride and calcium fluoride, is surrounded by many oppositely charged nearest neighbors, each ion is held fairly tightly in its allotted position. At room temperature each ion can vibrate slightly about its mean position, but much more energy must be added before an ion can move fast enough and far enough to begin to escape the attraction of its neighbors. Therefore a fairly high temperature is needed to melt an ionic compound. The melting points of some substances we have considered are: LiH, 680°C; NaCl, 801°C; CaF2, 1360°C. Once an ionic solid melts, the individual ions can move around, though most of the nearest neighbors of each anion will still be cations and vice versa. A characteristic feature of such a molten ionic compound is that it conducts electricity. If two wires are placed in the melt and are connected to a battery, the positive ions in the melt will gradually move toward the negatively charged wire, while the negative ions will move toward the positively charged wire. Movement of charged ions through the melt constitutes passage of an electrical current just as movement of electrons through a metal wire does. Its occurrence can be detected by an appropriate electrical meter.
Both the melting point of the solid and the electrical conductivity of the liquid provide valuable clues for deciding whether a compound is ionic or not. An interesting example of this is a comparison between aluminum fluoride, AlF3, and aluminum bromide, AlBr3. We find that AlF3 has a melting point of 1040°C, and the melt conducts electricity. By contrast AlBr3 melts at 97.5°C, and the melt does not conduct electricity. The obvious inference is that the former compound is ionic, while the latter is not.
The crystals of ionic substances are transparent, hard, brittle, and have characteristic shapes. They also are easily cleaved. This means that if a wedge-shaped instrument (such as a knife blade) is properly placed on a crystal and tapped sharply, the crystal will break cleanly in two. This can be seen in the following video:
When the knife is placed parallel to the planes of the crystal, it breaks the first crystal into two new crystals, with faces that are nearly perfect planes. Further, when the knife is not placed in line with the plane, but at a 45° angle, the crystal shatters instead of breaking evenly. Still, the cleanest break occurs along the plane of the crystal. Hardness of ionic crystals is a consequence of the strong coulombic forces which hold each ion in its allotted position. The shape and cleavage of a crystal are the result of the specific geometric arrangement of the ions in a crystal lattice. For example, since 90° angles occur between layers of ions in the microscopic lattice of NaCl ( and LiH), 90° angles are also reasonable in the macroscopic crystals of NaCl.(If you examine a few small crystals from a salt shaker, you will see that this is true-some are almost perfect cubes!) Thus characteristic shapes and cleavages may often be used to distinguish one ionic compound from another.
The following animation shows what is occurring on the atomic scale when the crystal of NaCl is cleaved.
When a large force is applied parallel to a layer of ions in the crystal lattice, it can shift that layer with respect to the next. Only a small shift is needed before positive ions in one layer are adjacent to positive ions in the other, and negative ions similarly become nearest neighbors. The two portions of the lattice repel one another and fall apart. On a macroscopic level the crystal cleaves, leaving flat faces corresponding to each layer of ions.
Perhaps the most important property of ionic solids is that most of them dissolve in water. Mute testimony to this is provided by the rows and rows of bottles in the average chemistry laboratory which contain aqueous ionic solutions. A characteristic feature of these solutions is that they all conduct electricity, showing that the ions retain their charges in solution and are also free to move about in it. When barium chloride, BaCl2, dissolves in water, for example, the Ba2+ and Cl– ions which were held tightly together in the crystal lattice become separated from each other in solution and can move about independently. If two wires are now immersed in this solution and attached to a battery, much the same thing happens as in the case of a molten salt. The Ba2+ ions are attracted by the negative charge on the one wire and move toward it, while the Cl– ions move toward the positive charge on the other wire. This flow of charges in the body of the solution is matched by a flow of electrons in the wire and can be measured by an appropriate meter.


