6.3: Energy and the Formation of Ions
- Page ID
- 49343
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Formation of an ion pair by transfer of an electron from an Li atom to an H atom results in an overall lowering of the total energy of the two nuclei and four electrons involved. How and why this occurs is best seen if we break ion-pair formation into three simpler steps and consider the energy change involved in each. The three steps are
- Removal of the 2s electron from an Li atom to form an Li+ ion.
- Addition of that same electron to an H atom to form an H– ion.
- The coming together of the two ions to form an ion pair.
The energy required in step 1 to remove an electron completely from an isolated atom is called the ionization energy. The ionization energy of lithium is 520 kJ mol–1. In other words, 520 kJ of energy is needed to remove a mole of 2s electrons from a mole of isolated lithium atoms in order to form a mole of isolated lithium ions. Alternatively we can say that 520 kJ is needed to ionize a mole of lithium atoms. See Figure \(\PageIndex{1}\) for a visual representation of the energy "cost" of ionization.
While energy is needed to accomplish step 1, we find that energy is released in step 2 when a hydrogen atom accepts an electron and becomes a hydride ion. The reason for this can be seen in the formation of LiH ion pair dot density diagram. The second electron acquired by the hydrogen atom can pair up with the electron already in the 1s orbital without contradicting the Pauli exclusion principle. As a result, the new electron can move in close enough to the hydrogen nucleus to be held fairly firmly, lowering its energy significantly. Although the paired electrons repel each other somewhat, this is not enough to offset the attraction of the nucleus for both.
Since the energy of the electron is lowered, the law of conservation of energy requires that the same quantity of energy must be released when a hydrogen atom is transformed into a hydride ion. The energy released when an electron is acquired by an atom is called the electron affinity. The electron affinity of hydrogen is 73 kJ mol–1 indicating that 73 kJ of energy is released when 1 mol of isolated hydrogen atoms each accepts an electron and is converted into a hydride ion.
Since 520 kJ mol–1 is required to remove an electron from a lithium atom, while 73 kJ mol–1 is released when the electron is donated to a hydrogen atom, it follows that transfer of an electron from a lithium to a hydrogen atom requires (520 – 73) kJ mol–1 = 447 kJ mol–1. This net energy change can best be seen in Figure \(\PageIndex{1}\).
At room temperature processes which require such a large quantity of energy are extremely unlikely. Indeed the transfer of the electron would be impossible if it were not for step 3, the close approach of the two ions. When oppositely charged particles move closer to each other, their potential energy decreases and they release energy. The energy released when lithium ions and hydride ions come together to 160 pm under the influence of their mutual attraction is 690 kJ mol–1, more than enough to offset the 447 kJ mol–1 needed to transfer the electron. Thus there is a net release of (690 – 447) kJ mol–1 = 243 kJ mol–1 from the overall process. The transfer of the electron from lithium to hydrogen and the formation of an Li+H– ion pair results in an overall lowering of energy, as seen in Figure \(\PageIndex{1}\) below.
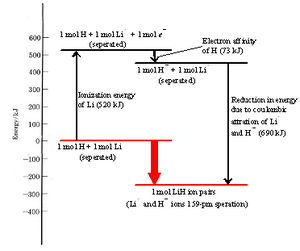
In the above figure, the energy change in each step and the overall change are illustrated diagrammatically. As in the case of atomic structure, where electrons occupy orbitals having the lowest allowable energy, a collection of atoms tends to rearrange its constituent electrons so as to minimize its total energy. Formation of a lithium hydride ion pair is energetically “downhill” and therefore favored.
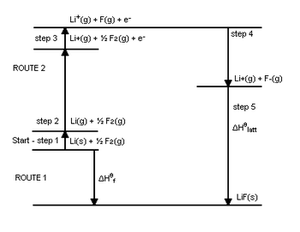
A more complete picture of the energies involved is provided by the "Born-Haber Cycle" diagram of LiF2 below. It emphasizes that the EA and IP apply to single atoms in the gas phase, and that other energies may be more important in determining the exothermicity of formation of ionic compounds. The greatest energy released is not the EA, but the lattice energy. Other energy costs involve formation of single atoms in the gas phase by vaporization of Li (s) (ΔHvap) to give Li (g), and the dissociation energy of F2 (ΔH dissociation) to give 2F. The sum of all the energies is the energy of formation of the ionic compound, according to Hess' Law. Basically, the Born Haber Cycle shows all the details of the formation of LiF2, while the diagram we looked at earlier takes a big picture view.
References
- Haber Cycle [en.Wikipedia.org]


