4.13: Transmutation and Radioactivity
- Page ID
- 49332
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Transmutation of one element into another requires a change in the structures of the nuclei of the atoms involved. For example, the first step in the spontaneous radioactive decay of uranium is emission of an α particle, \(\ce{ _{2}^{4}He^{2+}}\), from the nucleus \(\ce{_{92}^{238}U}\) Since the α particle consists of two protons and two neutrons, the atomic number must be reduced by 2 and the mass number by 4. The product of this nuclear reaction is therefore \(\ce{_{90}^{234}Th}\). In other words, loss of an α particle changes (transmutes) uranium into thorium. In the equation for the decay, the sum of the atomic numbers on the left and right are equal, as is the sum of the mass numbers on the left and right:
\[\ce {_{92}^{238}U \to _{90}^{234} Th} ^{*} + \ce{_{2}^{4} \alpha} \label{1} \]
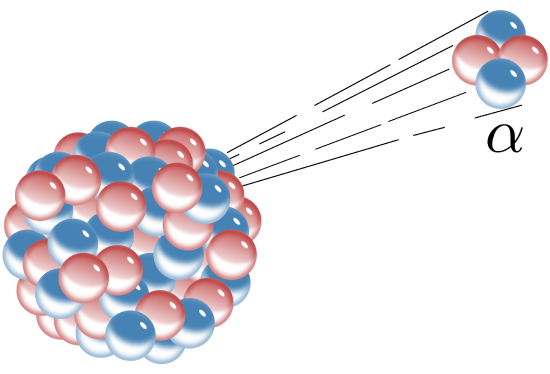
Alpha decay (Figure 4.12.1) is typical for large nuclei, because it reduces their size rapidly. Every element above Z = 83 (Bi) is radioactive, apparently because no number of neutrons can stabilize the nucleus against the repulsions between large numbers of protons.
Loss of a β particle (electron) from an atomic nucleus leaves the nucleus with an extra unit of positive charge, that is, an extra proton. This increases the atomic number by 1 and also changes one element to another. For example, the \({}_{\text{90}}^{\text{234}}\text{Th}\) mentioned above emits β particles. Its atomic number increases by 1, but its mass number remains the same. (The β particle is an electron and has a very small mass.) In effect one neutron is converted to a proton and an electron. Thus the thorium transmutes to protactinium \({}_{\text{91}}^{\text{234}}\text{Pa}\). (Note carefully that the β particle is an electron emitted from the nucleus of the thorium atom, not one of the electrons from outside the nucleus (Figure \(\PageIndex{2}\)) Using the standard symbol
\[{}_{\text{90}}^{\text{234}}\text{Th }\to \text{ }{}_{\text{91}}^{\text{234}}\text{Pa + }{}_{-\text{1}}^{\text{0}}\beta \nonumber \]
-
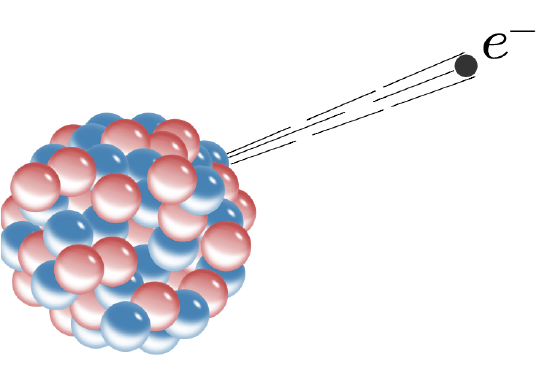
- Figure \(\PageIndex{2}\): The image above shows beta decay, which is the release of an electron from the nucleus after the conversion of a neutron into a proton and electron. The proton remains in the nucleus while the electron (or beta particle) is ejected.
Beta decay increases the number of protons, so it occurs when a nucleus has a high n/p ratio, compared to the stable nuclei of that element. If the nucleus has a low \(n/p\) ratio, it can reduce the number of protons by "positron" emission:
\[{}_{\text{6}}^{\text{11}}\text{C }\to \text{ }{}_{\text{5}}^{\text{11}}\text{B + }{}_{\text{+1}}^{\text{0}}\beta \nonumber \]
Positrons ( \({}_{\text{+1}}^{\text{0}}\beta\) ) are the basis of medical "PET (Positron Emission Tomography) Scans", in which they annihilate their antiparticle, the beta:
\[{}_{\text{+1}}^{\text{0}}\beta +{}_{\text{-1}}^{\text{0}}\beta \to 2 ~{}_{\text{0}}^{\text{0}}\gamma \nonumber \]
The two gammas leave in opposite directions from the point of the annihilation, so the PET machine can "trace" their origin to create an image.
A gamma ray is not a particle, and so its emission from a nucleus does not involve a change in atomic number or mass number. Rather it involves a change in the way the same protons and neutrons are packed together in the nucleus. In Equation \(\ref{1}\), the product Th is shown with an asterisk, indicating that the decay leaves it in an excited state. It releases its extra energy in the form of a gamma (Figure \(\PageIndex{3}\)):
\[{}_{\text{90}}^{\text{234}}\text{Th* }\to \text{ }{}_{\text{90}}^{\text{234}}\text{Th + }{}_{\text{0}}^{\text{0}}\gamma \nonumber \]
-
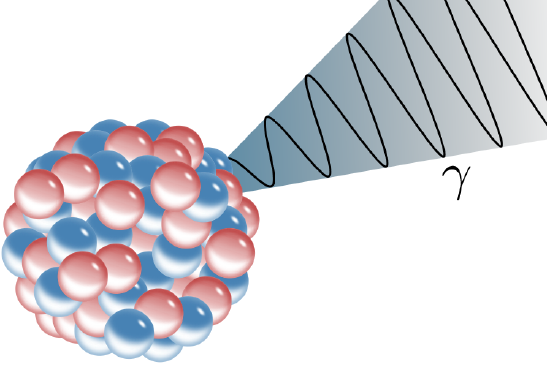
- Figure \(\PageIndex{3}\): The image above depicts gamma ray emission. The rearrangement of neutrons and protons in the nucleus causes the release of energy in the form of a gamma ray, seen above.
It is important to note, however, that radioactivity and transmutation both involve changes within the atomic nucleus. Such nuclear reactions will be discussed in more detail in the section devoted to Nuclear Chemistry. Because protons and neutrons are held tightly in the nucleus, nuclear reactions are much less common in everyday life than chemical reactions. The latter involve electrons surrounding the nucleus, and these are much less rigidly held.


