3.11.1: Biology- Solution Concentrations and Cells
- Page ID
- 50748
Solution concentration plays critical roles in biology:
-
- Differing concentrations of hydrogen ions on opposite sides of a membrane provide the driving force for synthesis of ATP, as shown by an animation.
- Nerve conduction depends on concentration gradients of Na+ and K+ ions inside and outside the nerve cell.
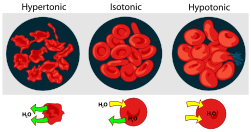
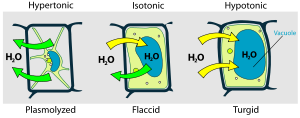
- Osmosis, caused by differing solution concentrations inside and outside of cells, can be fatal to both plants and animals. Putting a plant in salt water leads to wilting and plasmolysis in plants (see Figure), because water diffuses out of the cells. Freshwater fish die rapidly in salt water for the same reason. If intravenous fluids administered in surgery are not isotonic (having the same "Osmolar" concentration as plasma and red blood cells may be destroyed. If the I.V. solution is hypertonic (too high in concentration), red blood cells are deformed by crenation; if the I.V. is hypotonic (too low in concentration, red blood cells burst by "cytolysis, as shown below.
In the laboratory, in your body, and in the outside environment, the majority of chemical reactions take place in solutions. Macroscopically a solution is defined as a homogeneous mixture of two or more substances, that is, a mixture which appears to be uniform throughout. On the microscopic scale a solution involves the random arrangement of one kind of atom or molecule with respect to another.
There are a number of reasons why solutions are so often encountered both in nature and in the laboratory. The most common type of solution involves a liquid solvent which dissolves a solid solute. (The term solvent usually refers to the substance present in greatest amount. There may be more than one solute dissolved in it.) Because a liquid adopts the shape of its container but does not expand to fill all space available to it, liquid solutions are convenient to handle. You can easily pour them from one container to another, and their volumes are readily measured using graduated cylinders, pipets, burets, volumetric flasks, or other laboratory glass-ware. Moreover, atoms or molecules of solids dissolved in a liquid are close together but still able to move past one another. They contact each other more frequently than if two solids were placed next to each other. This “intimacy” in liquid solutions often facilitates chemical reactions.
Since solutions offer a convenient medium for carrying out chemical reactions, it is often necessary to know how much of one solution will react with a given quantity of another. Examples in other sections have shown that the amount of substance is the quantity which determines how much of one material will react with another. The ease with which solution volumes may be measured suggests that it would be very convenient to know the amount of substance dissolved per unit volume of solution. Then by measuring a certain volume of solution, we would also be measuring a certain amount of substance.
The concentration c of a substance in a solution (often called molarity) is the amount of the substance per unit volume of solution:
\[\text{Concentration of solute, M}=\frac{\text{amount of solute, mol}}{\text{volume of solution, L}} \nonumber \]
\[c_{\text{solute, M}}~=~\frac{n_{\text{solute, mol}}}{V_{\text{solution,L}}} \label{2} \]
Usually the units moles per cubic decimeter (mol dm–3) or moles per liter (mol liter–1) are used to express concentration.
If a pure substance is soluble in water, it is easy to prepare a solution of known concentration. A container with a sample of the substance is weighed accurately, and an appropriate mass of sample is poured through a funnel into a volumetric flask, as shown in Figure 3.3. The container is then reweighed. Any solid adhering to the funnel is rinsed into the flask, and water is added until the flask is about three-quarters full. After swirling the flask to dissolve the solid, water is added carefully until the bottom of the meniscus coincides with the calibration mark on the neck of the flash.
|
Isotonic saline solution for medical applications is made according to the method above. The container and sodium chloride weigh 43.2874 g and the final mass after pouring was 41.0374 g. The flask has a volume of 250 mL.
Solution
The concentration can be calculated by dividing the amount of solute by the volume of solution [Eq. (1)]:
-
- \(c_{\text{NaCl}}=\frac{n_{\text{NaCl}}}{V}\)
nNaCl = 2.2500 g × \(\frac{\text{1 mol}}{\text{58}\text{.44 g}}\) = 3.850 × 10-2 mol
The volume of solution is 250.00 ml, or Vsolution = 250.00 cm3 × \(\frac{\text{1 dm}^{\text{3}}}{\text{10}^{\text{3}}\text{ cm}^{\text{3}}}\) = 2.5000 × 10-1 dm3 or .250 L Thus \(c_{\text{NaCl}}=\frac{n_{\text{NaCl}}}{V_{\text{solution}}}=\frac{\text{3}\text{.850}\times \text{10}^{\text{-2}}\text{ mol }}{\text{250}\text{.00 }\times \text{10}^{\text{-1}}\text{ dm}^{\text{3}}}=\text{1}\text{.540 }\times 10^{^{\text{-1}}}\text{mol dm}^{\text{-3}}\) = 0.1540 mol L-1Isotonic saline solutions have the same "osmolarity" as blood plasma, so they are isotonic with it and red blood cells. Isotonic intravenous saline is 9 g NaCl in 1000 mL water, or roughly 0.15 M NaCl, as we see above. Its osmolarity is 0.30 Osm ("osmolar"), because each of the two ions, Na+ and Cl- affect osmosis, and 0.15 M NaCl gives 0.30 M total concentration of ions.
Note that the definition of concentration is entirely analogous to the definitions of density, molar mass, and stoichiometric ratio that we have previously encountered. Concentration will serve as a conversion factor relating the volume of solution to the amount of dissolved solute.
\(\text{Volume of solution}\overset{concentration}{\longleftrightarrow}\text{amount of solute}\) \(V\overset{c}{\longleftrightarrow}n\) Because the volume of a liquid can be measured quickly and easily, concentration is a much-used quantity. The next two examples show how this conversion factor may be applied to commonly encountered solutions in which water is the solvent (aqueous solutions).
There are various IV fluids used in hospitals. "D5W" only contains glucose; NS only contains Sodium Chloride; LR Solution contains Sodium, Chloride, Lactate, Potassium, and Calcium. If D5W[1] has a concentration of 0.2520 mol dm–3, what amount (in mol) of glucose is administered to a patient in 24.71 cm3 (24.71 ml) of this solution?
Solution
Using concentration as a conversion factor, we have
-
- \(V\text{ }\xrightarrow{c}\text{ }n\)
\(=\text{24}\text{.71 cm}^{\text{3}}\times \frac{\text{0}\text{.2520 mol}}{\text{1 dm}^{\text{3}}}\times \frac{\text{1 dm}^{\text{3}}}{\text{10}^{\text{3}}\text{ cm}^{\text{3}}}\)
= 0.006 227 mol
Alternatively, 24.71 mL x \(\frac{\text{1 liter}}{\text{1000 mL}} x \frac{\text{0.2520 mol}}{liter} = \text{0.006227 mol}\)
The concentration units of moles per cubic decimeter are often abbreviated M, pronounced molar. That is, a 0.1-M (one-tenth molar) solution contains 0.1 mol solute per cubic decimeter of solution. This abbreviation is very convenient for labeling laboratory bottles and for writing textbook problems; however, when doing calculations, it is difficult to see that \(\text{1 dm}^{\text{3}}\times \text{1 }\text{M}=\text{1mol}\) Therefore we recommend that you always write the units in full when doing any calculations involving solution concentrations. That is,
\(\text{1 dm}^{\text{3}}\times \text{1 }\dfrac{\text{mol}}{\text{dm}^{\text{3}}}=\text{1mol}\)
\(\text{1 L}\times \text{1 }\dfrac{\text{mol}}{\text{L}}=\text{1mol}\)
Problems such as Example 2 are easier for some persons to solve if the solution concentration is expressed in millimoles per cubic centimeter (mmol cm–3) instead of moles per cubic decimeter. Since the SI prefix m means 10–3, 1 mmol = 10–3 mol, and
\(\text{1 M} ~ = ~ \dfrac{\text{1 mol}}{\text{1 dm}^{\text{3}}} ~ \times ~ \dfrac{\text{1 dm}^{\text{3}}}{\text{1 L}} ~ = ~ \dfrac{\text{1 mol}}{\text{L}}\)
\(\text{1 M} ~ = ~ \dfrac{\text{1 mol}}{\text{L}} ~ \times ~ \dfrac{\text{10}^{\text{-3}}\text{ L}}{\text{1 ml}} ~ \times ~ \dfrac{\text{1 mmol}}{\text{10}^{\text{-3}}\text{ mol}} ~ = ~ \dfrac{\text{1 mmol}}{\text{1 ml}}\)
\(\text{1 M} ~ = ~ \dfrac{\text{1 mol}}{\text{1 dm}^{\text{3}}} \times \dfrac{\text{1 dm}^{\text{3}}}{\text{10}^{\text{3}}\text{ cm}^{\text{3}}} \times \dfrac{\text{1 mmol}}{\text{10}^{\text{-3}}\text{ mol}} ~ = ~ \dfrac{\text{1 mmol}}{\text{1 cm}^{\text{3}}} \)
Thus a concentration of 0.1396 mol dm–3 (0.1396 M) can also be expressed as 0.1396 mmol cm–3. Expressing the concentration this way is very convenient when dealing with laboratory glassware calibrated in milliliters or cubic centimeters.
Exactly 250 ml of NS (Normal Saline) I.V. solution whose concentration is 0.154 M in NaCl was delivered from a pipet. (a) What amount of NaCl was present? (b) What mass of NaCl would remain if all the water evaporated?
Solution
a) Since 0.154 M means 0.154 mol dm–3, or 0.154 mmol cm–3, we choose the latter, more convenient quantity as a conversion factor:
\(n_{\text{NaCl}}=\text{250}\text{.0 cm}^{\text{3}}\times \frac{\text{0}\text{.154 mol}}{\text{1 cm}^{\text{3}}}=\text{38}\text{.5 mmol}=\text{38}\text{.5}\times 10^{\text{-3}}\text{ mol}\) b) Using molar mass, we obtain \(\text{m}_{\text{NaCl}}=\text{38}\text{.5}\times 10^{\text{-3}}\text{ mol}\times \frac{\text{58}\text{.443 g}}{\text{1 mol}}=2.\text{25}\text{g}\) Note: The symbols nNaCl and mNaCl refer to the amount and mass of the solute NaCl, respectively. They do not refer to the solution. If we wanted to specify the mass of aqueous NaOH solution, the symbol mNaCl(aq) could be used.From ChemPRIME: 3.10: Solution Concentrations










