3.4.1: Environment- Synthesis of Biodiesel Fuel
- Page ID
- 50053
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Biological oils are different from petroleum oils ("regular" diesel fuel) in molecular structure and properties.

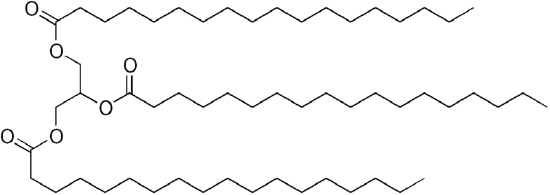
Common petroleum diesel fuel is a mixture of simple hydrocarbons, with the average chemical formula C12H23 (shown below), but components may range approximately from C10H20 (dodecane) to C15H28(pentadecane).[1] By contrast, biological oils are "triglycerides" (classified as "esters") like the glyceryl trilinoleate shown below:
C12H23, dodecane |
A triglyceride: glyceryl trilinoleate |
Because of their large size and consequent large intermolecular attractions, the viscosity of biological oils is generally too high for use in conventional diesel engines. Biological oils also burn a little less readily, and with a sootier flame than petroleum diesel. Biological oils can be used in conventional diesel engines if they are preheated to reduce their viscosity, but this requires an auxiliary electrical heater until the engine warms up. For these resons, bilogical oils require processing for use as biodiesel.
A biological oil is an ester, which is a type of organic compound having the atom linkage shown below.
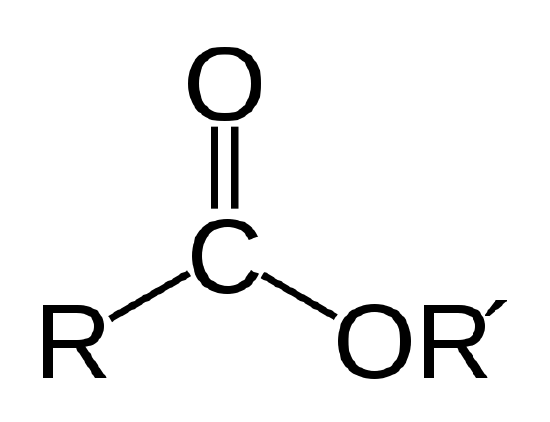 The ester linkage. R and R' represent chains of carbon and hydrogen atoms. R = -CH3 and R' = -C18H35O2 for the methyl stearate in Example 1 |
glycerol |
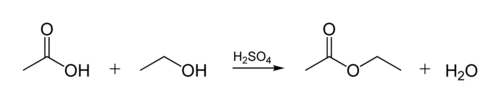
The ester linkage in biological oils is created when a glycerol molecule reacts with organic acids. The glycerol molecule has a chain of 3 carbon atoms, each with an -OH (alcohol) group on it. The figure below shows how an organic alcohol reacts with a organic acid. Organic chemists abbreviate molecular structures--the "zig-zag" lines in the figure represent carbon chains with a C atom at each "zig" or "zag". Each carbon has 4 bonds, and if fewer than 4 are shown, it's assumed that they go to H atoms. So the alcohol is C2H5OH (ethanol), and the acid is acetic acid (or ethanoic acid, CH3COOH) in the Figure:
Since glycerol has 3 -OH groups, 3 long chain organic "fatty acids" attach to make the bulky "triglyceride".
But just as easily as esters can be made from alcohols and acids, they can switch alcohols or acids. In the presence of a strong base catalyst, like NaOH, a triglyceride can react with 3 small alcohol molecules, like methanol (CH3OH), which replace the glycerol "backbone", making 3 separate esters of lower molecular weight
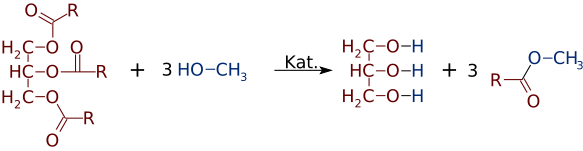
Quite often a mixture of two or more products is formed. For example, when a vegetable oil reacts with methanol, only one or two of the acids may be displaced from the glycerine, producing only 1 or 2 FAMEs.
- C3H5(C18H35O2)3 + NaOH + 2 CH3OH → C3H5(C18H35O2)2(OH) + 2 C17H35COOCH3
- C3H5(C18H35O2)3 + NaOH + 1 CH3OH → C3H5(C18H35O2)(OH)2 + 1 C17H35COOCH3
- C3H5(C18H35O2)3 + NaOH + 3 CH3OH → C3H5(OH)3 + 3 C17H35COOCH3
Usually, a large excess of methanol and sodium hydroxide are added, so that the reaction produces the maximum amount of FAME.
But in the case of a transesterification, even though none of the reactants is completely consumed, no further increase in the amounts of the products occurs. We say that such a reaction does not go to completion. When a mixture of products is produced or a reaction does not go to completion, the effectiveness of the reaction is usually evaluated in terms of percent yield of the desired product. A theoretical yield is calculated by assuming that all the limiting reagent is converted to product. The experimentally determined mass of product is then compared to the theoretical yield and expressed as a percentage:
\(\text{Percent yield}=\frac{\text{actual yield}}{\text{theoretical yield}}\times \text{100 percent}\)
EXAMPLE 1 When 100.0 g C3H5(C18H35O2)3 gas and 15.0 g CH3OH are mixed at 55°C with NaOH catalyst, they react to form 90.96 g C17H35COOCH3 methyl stearate biodiesel. Calculate the percent yield.
Solution
We must calculate the theoretical yield of NH3, and to do this, we must first discover whether N2 or H2 is the limiting reagent. For the balanced equation
- C3H5(C18H35O2)3 + NaOH + 3 CH3OH → C3H5(OH)3 + 3 C17H35COOCH3
- stearin + sodium hydroxide + 3 CH3OH → glycerol + 3 methyl stearate
The stoichiometric ratio of the reactants is
\(\text{S}\left( \frac{\text{stearin}}{\text{CH}_{\text{3}}\text{OH}} \right)=\frac{\text{1 mol stearin}}{\text{3 mol CH}_{\text{3}}\text{OH}}\) Now, the initial amounts of the two reagents are and \(\begin{align} & n_{\text{stearin}}\text{(initial)}=\text{100}\text{.0 g stearin}\times \frac{\text{1 mol stearin}}{\text{891}\text{.5 stearin}}=\text{0}\text{.1122 mol stearin} \\ & \\ & n_{\text{CH}_{\text{3}}\text{OH}}\text{(initial)}=\text{15}\text{.0 g CH}_{\text{3}}\text{OH}\times \frac{\text{1 mol CH}_{\text{3}}\text{OH}}{\text{32}\text{.04 g CH}_{\text{3}}\text{OH}}=\text{0}\text{.4682 mol CH}_{\text{3}}\text{OH} \\ \end{align}\) The ratio of initial amounts is thus \(\frac{n_{\text{stearin}}\text{(initial)}}{n_{\text{CH}_{\text{3}}\text{OH}}\text{(initial}}~=~ \frac{\text{0}\text{.1122 mol stearin}}{\text{0}\text{.4682 mol CH}_{\text{3}}\text{OH}}~=~\frac{\text{0}\text{.240 mol stearin}}{\text{1 mol CH}_{\text{3}}\text{OH}}\) Since this ratio is less than \(\text{S}\left( \frac{\text{stearin}}{\text{CH}_{\text{3}}\text{OH}} \right)~=~0.33\), there is an excess of CH3OH. Stearin is the limiting reagent. Accordingly we must use 0.1122 mol stearin and 0.3366 mol CH3OH (rather than 0.4682 mol CH3OH) to calculate the theoretical yield of C17H35COOCH3 (methyl stearate). We then have \(n_{\text{methyl stearate}}\text{(theoretical)}=\text{0}\text{.1122 mol stearin}\times \frac{\text{3 mol methyl stearate}}{\text{1 mol stearin}}=\text{0}\text{.3365 mol methyl stearate}\) so that \(\text{m}_{\text{methyl stearate}}\text{(theoretical)}=\text{0}\text{.3365 mol methyl stearate}\times \frac{\text{298}\text{.51 g methyl stearate}}{\text{1 mol methyl stearate}}=\text{100}\text{.5 g methyl stearate}\) We can organize these calculations in a table:
| C3H5(C18H35O2)3(s) | + 3 CH3OH (l) | → 1 C3H5(OH)3 (l) | + 3 C18H35O2)3CH3(s) | ||
|---|---|---|---|---|---|
| m, g | 100.0 g | 15.00 g | 90.96 g | ||
| M, g/mol | 891.5 | 32.04 | 298.5 | 92.1 | |
| n present, mol | 0.1122 mol | 0.4682 mol | |||
| n actual, mol | 0.1122 | 0.3366 | 0.1122 | 0.3366 | |
| m actual, mass | 100.0 | 10.78 | 10.33 | 100.47 |
The percent yield is then \(\text{Percent yield}=\frac{\text{actual yield}}{\text{theoretical yield}}\times \text{100 percent }=\frac{\text{90}\text{.96 g}}{\text{100}\text{.5 g}}\times \text{100 percent}=\text{90}\text{.55 percent}\)
Transesterification is a classic example of a reaction which does not go to completion.
References
- en.Wikipedia.org/wiki/Diesel_fuel


