1.6: Measurements, Quantities, and Unity Factors
- Page ID
- 49274
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Measurements
Let us assume that you are faced with a specific problem. Then we can see how scientific thinking might help solve it. Suppose that you live near a large plant which manufactures cement. Smoke from the plant settles on your car and house, causing small pits in the paint. You would like to stop this air-pollution problem—but how?
As an individual you will probably have little influence, and even as part of a group of concerned citizens you may be ineffective, unless you can prove that there is a problem. Scientists have had a hand in writing most air-pollution regulations, and so you will have to employ some scientific techniques (or a scientist) to help solve your problem.
It will probably be necessary to determine how much air pollution the plant is producing. This might be done by comparing the smoke with a scale which ranges from white to gray to black, the assumption being that the darker the smoke, the more there is. For white cement dust, however, this is much less satisfactory than for black coal smoke. A better way to determine how much pollution there is would be to measure the mass of smoke particles which could be collected near your house or car. This could be done by using a pump (such as a vacuum cleaner) to suck the polluted gas through a filter. Weighing the filter before and after such an experiment would determine what mass of smoke had been collected.
Mass and Weight
Because weight is the force of gravity on an object, which varies from place to place by about 0.5% as shown in the Table, we must use mass for accurate measurements of how much matter we have. We still call the process of obtaining an accurate mass "weighing".
| Latitude, o | Altitude = 0 | Altitude = 10 km |
|---|---|---|
| 0 | 9.78036 | 9.74950 |
| 30 | 9.79324 | 9.76238 |
| 60 | 9.81911 | 9.78825 |
| 90 | 9.83208 | 9.80122 |
The weight of an object is actually the force of gravity, and is calculated as
\[F=\text{“W”}=m \times g \label{1} \]
Weight is measured in newtons (kg m s-2) or pounds (lb), where 1 lb = 4.44822162 newtons. The base unit for mass is kilograms (kg), but the pound may also be used as a unit of mass (1 pound = 0.45359237 kilograms). The average value of g is usually taken to be 9.80665 m s-2, so the weight of a 1 kg mass would be
\[F = \text{ “W” } = m \times g = 1 \text{ kg} \times 9.80665 \text{ m s}^{-2} = 9.80665 \text{ N or } 2.2046 \text{ lb} \nonumber \]
If the weight of the 1 kg mass were measured on an arctic exploration camp with a load cell balance (see below) still calibrated for the average g, its weight would be:
\[ F = \text{ “W” } = m \times g = 10 \text{ kg} \times 9.83208 \text{ m s}^{-2} = 9.83208 \text{ N or } 2.2103 \text{ lb} \nonumber \]
Accurate weighing is usually done with a single pan balance. The empty pan is balanced by a counterweight. When an object is placed on the pan, gravitational attraction forces the pan downward. To restore balance, a series of weights (objects of known mass) are removed from holders above the pan. The force of gravitational attraction is proportional to mass, and when the pan is balanced, the force on it must always be the same. Therefore the mass of the object being weighed must equal that of the weights that were removed. A balance gives the same mass readout regardless of the force of gravity.

Modern laboratory "balances" are based on load cells that convert the force exerted by an object on the balance pan to an electrical signal. The load cell generally is coupled with a dedicated converter and digital display. Because the force exerted by the object depends on gravity, these are really scales that measure weight, and must be calibrated frequently (against standard masses) to read a mass.
Mass Measurements
If you kept a notebook or other record of your measurements, you would probably write down something like 0.0342 g to represent how much smoke had been collected. Such a result, which describes the magnitude of some parameter (in this case the magnitude of the parameter, mass), is called a quantity. Notice that it consists of two parts, a number and a unit. It would be ambiguous to write just 0.0342—you might not remember later whether that was measured in units of grams, ounces, pounds, or something else. A quantity always behaves as though the number and the units are multiplied together. For example, we could write the quantity already obtained as 0.0342 × g. Using this simple rule of number × units, we can apply arithmetic and algebra to any quantity:
\[\begin{align} & 5 \text{g} + 2 \text{g} = (5 + 2) \text{g} = 7 \text{g} \\ & 5 \text{g} \div 2 \text{g} = \dfrac{5 \text{g}}{2 \text{g}} = 2.5 \text{ (the units cancel, and so we get a pure number)} \\ & 5 \text{ in} \times 2 \text{ in} = 10 \text{ in}^{2} \text{ (10 square inches)}\end{align} \nonumber \]
This works perfectly well as long as we do not write equations with different parameters (i.e., those having units which measure different properties, like mass and length, temperature and energy, or volume and amount) on opposite sides of the equal sign. For example, applying algebra to the equation
\[ 5 \text{g} = 2 \text{ in}^{2} \nonumber \]
can lead to trouble in much the same way that dividing by zero does and should be avoided, because grams (g) is a unit of the parameter mass, and the inch (in) is a unit of the parameter length.
Conversions with Unity Factors
Mass Unity Factors
Notice also that whether a quantity is large or small depends on the size of the units as well as the size of the number. For example, the mass of smoke has been measured as 0.0342 g, but the balance might have been set to read in milligrams (or grains in the English system). Then the reading would be 34.2 mg (or 0.527 grains). The results (0.0342 g, 34.2 mg, or 0.527 gr) are the same quantity, the mass of smoke. One involves a smaller number and larger unit (0.0342 g), while the others have a larger number and smaller unit. So long as we are talking about the same quantity, it is a simple matter to adjust the number to go with any units we want.
We can convert among the different ways of expressing the mass with unity factors as follows:
Since 1 mg and 0.001 g are the same parameter (mass), we can write the equation
\[ 1 \text{ mg} = 0.001 \text{ g} \nonumber \]
Dividing both sides by 1 mg, we have
\[1 = \dfrac{1\text{ mg}}{1\text{ mg}} = \dfrac{0.001\text{ g}}{1\text{ mg}} \nonumber \]
Since the last term of this equation equals one, it is called a unity factor. It can be multiplied by any quantity, leaving the quantity unchanged.
We can generate another unity factor by dividing both sides by 0.001 g:
\[1 = \dfrac{1\text{ mg}}{0.001\text{ g}} = \dfrac{0.001\text{ g}}{0.001\text{ g}} \nonumber \]
What is the mass in grams of a 5.0 grain (5 gr) aspirin tablet, given that 1 gram = 15.4323584 grains?
Solution:
\[ 5.0 \text{ gr} = 5.0 \text{ gr} \times 1 = 5.0 \text{ gr}\times \dfrac{1.0\text{ g}}{\text{15.4323 gr}} \nonumber \]
The units gr cancel, yielding the result
\[ 5.0 \text{ gr} = 5.0 \div 15.4323 \text{ g} = 0.324 \text{ g} \nonumber \]
Length Unity Factors
The parameter length may be measured in inches (in) in the English system, but scientific measurements (all measurements in the world exclusive of the U.S.) are reported in the metric units of meters (m) or some more convenient derived unit like centimeters (cm).
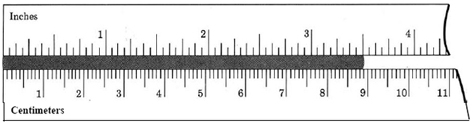
Express the length 8.89 cm in inches, given that 1 cm = 0.3937 in.
Solution
Since 1 cm and 0.3937 in are the same quantity, we can write the equation
\[1 \text{ cm} = 0.3937 \text{ in} \nonumber \]
Dividing both sides by 1 cm, we have
\[1 = \dfrac{0.3937\text{ in}}{1\text{ cm}} \nonumber \]
Since the right side of this equation equals one, it is called a unity factor. It can be multiplied by any quantity, leaving the quantity unchanged.
\[ 8.89 \text{ cm} = 8.89 \text{ cm} \times 1 = 8.89 \text{ cm} \times \dfrac{0.3937\text{ in}}{\text{1 cm}} \nonumber \]
The units centimeter cancel, yielding the result 8.89 cm = 8.89 × 0.3937 in = 3.50 in
This agrees with the direct observation made in the figure.
Let us look at our air-pollution problem. It has probably already occurred to you that simply measuring the mass of smoke collected is not enough. Some other variables may affect your experiment and should also be measured if the results are to be reproducible. For example, wind direction and speed would almost certainly be important. The time of day and date when a measurement was made should be noted too. In addition you should probably specify what kind of filter you are using. Some are not fine enough to catch all the smoke particles.
Temperature
Another variable which is almost always recorded is the temperature. A thermometer is easy to use, and temperature can vary a good deal outdoors, where your experiments would have to be done.
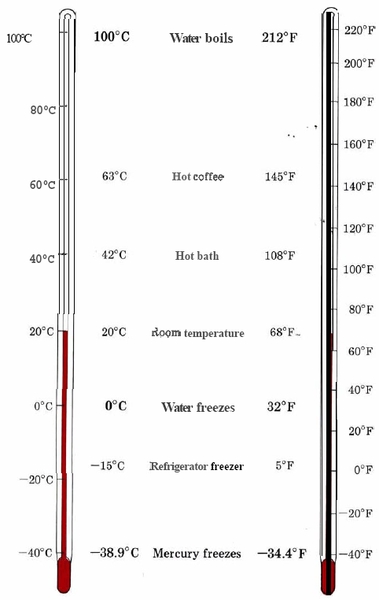

In scientific work, temperatures are usually reported in degrees Celsius (°C), a scale in which the freezing point of pure water is 0°C and the normal boiling point 100°C. In the United States, however, you would be more likely to have available a thermometer calibrated in degrees Fahrenheit (°F). The relationship between these two scales of temperature is
\[\dfrac{\text{T}_{(^{o}\text{F)}} - 32}{\text{T}_{(^{o}\text{C)}}}=\dfrac{9}{5} \nonumber \]
Note that the temperature scales cannot be interconverted with simple unity factors, because they do not have a common zero point (0°C = 32°F). Rather, the mathematical function above must be used. The equation above is written in terms of the parameter temperature (T) with the units or dimensions subscripted in parentheses.
Volume Measurements
More important than any of the above variables is the fact that the more air you pump through the filter, the more smoke you will collect. Since air is a gas, it is easier to measure how much you collect in terms of volume than in terms of mass, and so you might decide to do it that way. Running your pump until it had filled a plastic weather balloon would provide a crude, inexpensive volume measurement. Assuming the balloon to be approximately spherical, you could measure its diameter and calculate its volume from the formula
\[V=\dfrac{4}{3}\pi r^{3} \nonumber \]
Calculate the volume of gas in a sphere whose diameter is 106 in. Express your result in cubic centimeters (cm3).
Solution
Since the radius of a sphere is half its diameter,
\[ r = \dfrac{1}{2} \times 106 \text{ in} = 53 \text{ in} \nonumber \]
We can use the same equality of quantities as in Example 1 to convert the radius to centimeters. When we cube the number and units, our result will be in cubic centimeters.
\[ 1 \text{ cm} = 0.3937 \text{ in} \nonumber \]
\[\dfrac{\text{1 cm}}{\text{0}\text{.3937 in}} = 1 \nonumber \]
\[ R = 53 \text{ in} \times \dfrac{\text{1 cm}}{\text{0}\text{.3937 in}} = \dfrac{\text{53}}{\text{0}\text{.3937}} \text{ cm} \nonumber \]
Using the formula
\[\begin{align} & V =\dfrac{\text{4}}{\text{3}}\pi r^{\text{3}}=\dfrac{\text{4}}{\text{3}}\times \text{3}\text{.14159}\times ( \dfrac{\text{53}}{\text{0}\text{.3937}}\text{cm} )^{3} \\ & \text{ }=\text{10219264 cm}^{\text{3}} \\ & \end{align} \nonumber \]
You can see from Examples 1 and 2 that two unity factors may be obtained from the equality
\[ 1 \text{ cm} = 0.3937 \text{ in} \nonumber \]
We can use one of them to convert inches to centimeters and the other to convert centimeters to inches. The correct factor is always the one which results in cancellation of the units we do not want.
The result in Example 2 also shows that cubic centimeters are rather small units for expressing the volume of the balloon. If we used larger units, as shown in the following example, we would not need more than 10 million of them to report our answer.
Express the result of Example 3 in cubic meters, given that 1 m = 100 cm.
Solution
Again we wish to use a unity factor, and since we are trying to get rid of cubic centimeters, centimeters must be in the denominator:
\[\text{1 = }\dfrac{\text{1 m}}{\text{100 cm}} \nonumber \]
But this will not allow cancellation of cubic centimeters. However, note that 13 = 1 That is, we can raise a unity factor to any power, and it remains unity. Thus
\[\begin{align} & \text{1 =}\left( \text{ }\dfrac{\text{1 m}}{\text{100 cm}} \right)^{\text{3}}\text{ = }\dfrac{\text{1 m}^{\text{3}}}{\text{100}^{\text{3}}\text{ cm}^{\text{3}}}\text{ = }\dfrac{\text{1 m}^{\text{3}}}{\text{1 000 000 cm}^{\text{3}}} \\ \text{ and } \\ & \text{10 219 264 cm}^{\text{3}}\text{ = 10 219 264 cm}^{\text{3}}\text{ }\times \text{ }\left( \dfrac{\text{1 m}}{\text{100 cm}} \right)^{\text{3}} \\ & \text{ = 10 219 264 cm}^{\text{3}}\text{ }\times \text{ }\dfrac{\text{1 m}^{\text{3}}}{\text{100 000 cm}^{\text{3}}} \\ & \text{ = 10.219 264 m}^{\text{3}} \\ & \end{align} \nonumber \]


