8.8: Solutions to Selected Problems
- Page ID
- 203547
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 8.1.1:
- \(A = \varepsilon c l = 6 \frac{L}{mol \: cm} \times 0.01 \frac{mol}{L} \times 1 cm = 0.60 = 60 \%\)
- \(A = \varepsilon c l = 3000 \frac{L}{mol \: cm} \times 3.5 \times 10^{-5} \frac{mol}{L} \times 1 cm = 0.105 = 10.5 \%\)
- \(A = \varepsilon c l = 1.4 \frac{L}{mol \: cm} \times 0.25 \frac{mol}{L} \times 0.5 cm = 0.175 = 17.5 \%\)
- \(A = \varepsilon c l = 23000 \frac{L}{mol \: cm} \times 2.5 \times 10^{-6} \frac{mol}{L} \times 1 cm = 0.0575 = 5.75 \%\)
- \(A = \varepsilon c l = 14000 \frac{L}{mol \: cm} \times 0.015 \frac{mmol}{L} \times 1 cm = 14000 \frac{L}{mol \: cm} 0.015 \times 10^{3-} \frac{mol}{L} \times 1 cm = 0.21 = 21 \% \)
Exercise 8.1.2:
- \( \varepsilon= \frac{A}{cl} = \frac{0.30}{(0.01 mol \: L^{1-} \times 1 cm)} = 30 \frac{L}{mol \: cm}\)
- \( \varepsilon = \frac{A}{cl} = \frac{0.25}{(0.025 mol \: L^{-1} \times 1cm)} = 10 \frac{L}{mol \: cm}\)
- \( \varepsilon = \frac{A}{cl} = \frac{0.30}{(0.01 mol \: L^{-1} \times 1cm)} =543 \frac{L}{mol \: cm}\)
- \( \varepsilon = \frac{A}{cl} = \frac{0.66}{(0.025 mmol \: L^{-1} \times 1cm)} = 26400 \frac{L}{mol \:cm}\)
Exercise 8.1.3:
- blue
- red
- orange
- violet
- green
Exercise 8.1.4:
- \(E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{1 \times 10^{-5}m} = 1.98 \times 10^{-20} J\)
- \(E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{-8} m \: s^{-1})}{125 \times 10^{-9}m} = 1.59 \times 10^{-18} J\)
- \(E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{-8} m \: s^{-1})}{1025 \times 10^{-9}m} = 1.94 \times 10^{-19}J\)
- \(E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{450 \times 10^{-6}m} = 4.42 \times 10^{-22}J\)
- \(E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{-8} m \: s^{-1})}{850 \times 10^{-10}m} = 2.3 \times 10^{-18}J\)
Exercise 8.1.5:
- \(\lambda = \frac{hc}{E} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{-8} m \: s^{-1})}{1.46 \times 10^{-17} J} =1.36 \times 10^{-8} m\)
- \(\lambda = \frac{hc}{E} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{-8} m \: s^{-1})}{4.72 \times 10^{-24} J} =4.21 \times 10^{-2} m\)
- \(\lambda = \frac{hc}{E} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{-8} m \: s^{-1})}{9.26 \times 10^{-17} J} =2.15 \times 10^{-19} m\)
Exercise 8.1.6:
- \(E = h \nu = \frac{hc}{\lambda}\); so \(v = \frac {c}{\lambda}\); or \(\lambda = \frac{c}{v} = \frac{3.0 \times 10^{8} m \: s^{-1}}{6.7 \times 10^{10} s^{-1}}=4.48 \times 10^{-3} m \)
- \( \lambda = \frac{c}{v} = \frac{3.0 \times 10^{8} m \: s^{-1}}{1500 \times 10^{6} s^{-1}} = 0.2m\)
- \(v = \frac{c}{\lambda} = \frac{3.0 \times 10^{8} m \: s^{-1}}{9.8 \times 10^{-10}m} = 3.06 \times 10^{15} s^{-1}\)
- \(v \frac{c}{\lambda} = \frac{3.0 \times 10^{8} m \: s^{-1}}{4.3 \times 10^{-12}m}= 7.0 \times 10^{19} s^{-1}\)
Exercise 8.1.7:
a) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js \:mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{(1mm \times 10^{-3}m \: mm^{-1})} = 1.99 \times 10^{-22}J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 1.99 \times 10^{-22} J \times 6.02 \times 10^{23} mol^{-1} = 120 J mol^{-1} = 0.12 kJ \: mol^{-1}\)
b) \(E = \frac{hc}{lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 times 10^{8} m \: s^{-1})}{(1000nm \times 10^{-9} m \: nm^{-1})} = 1.99 \times 10^{-19}J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 1.99 \times 10^{-19} J \times 6.02 \times 10^{23} mol^{-1} = 120000 J \: mol^{-1} = 120 kJ \: mol^{-1}\)
c) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{(1m)} = 1.99 \times 10^{-25} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 1.99 \times 10^{-25} J \times 6.02 \times 10^{23} mol^{-1} = 0.120 J \: mol^{-1} = 1.2 \times 10^{-4} kJ \: mol^{-1} \)
d) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js mol^{-1} \times 3.0 \times 10^{8} m s^{-1})} = {(500 nm \times 10^{-9} m \: nm^{-1})} = 3.98 \times 10^{-19} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 3.98 \times 10^{-19} J \times 6.02 \times 10^{23} mol^{-1} = 239000 J mol^{-1} = 239 kJ\: mol^{-1}\)
Exercise 8.1.8:
Blue.
Exercise 8.1.9:
Ultraviolet light, with a shorter wavelength than visible light, is much higher in energy and potentially more damaging.
Exercise 8.2.3:
- \(d \rightarrow d\)
- \( \pi \rightarrow \pi * \)
- MLCT
Exercise 8.2.4:
- The one on the left can relax by channelling some energy into molecular vibration, especially its cis-trans isomerisation. The one on the right can't do that because its rotation is restricted by the presence of the ring.
- Of course! It's crawling with pi bonds. A strong pi-pi* transition in the visible region seems likely.
- Probably not. It does not have restricted rotation, so the cis-trans isomerisation route is available for relaxation.
- \(A = \varepsilon bc\) ; so \( \varepsilon = \frac{A}{bc} = \frac{0.77}{1cm \times 10^{-6}M} = 7.7 \times 10^{5} M^{-1} cm^{-1}\)
- That's a large molar absorptivity constant. It's allowed.
- Undoubtedly this is that pi-pi* transition we were thinking about earlier.
- If the compound binds to zinc, it probably does so via bidentate coordination. The resulting ring restricts the degrees of freedom in the compound so it can't undergo cis-trans isomerisation, closing off a route to rapid relaxation.
i) A compound like this could be used to detect metal ions such as Zn2+. Because the amount of fluorescence depends strongly on the Zn2+ concentration, it could be used to measure the amount of the ion present.
Exercise 8.2.5:
a)
b) An orange complex would absorb blue light, its complementary colour.
c) A blue laser would work. Maybe somewhere around 476 nm.
d) Notice a Re(II) site results, because it has transferred an electron to the ligand.
e)
f) The reduction potentials (1.4 V > 0.3 V) suggest transfer from copper (I) to rhenium (II).
g) i) The carbonyl stretches would be observed somewhere around 2000 cm-1.
iii) The electron transfer from the Cu(I) to the Re(II) site would result in a Re(I) site. The carbonyl stretch would shift to a lower wavenumber. That is because the lower oxidation state on the metal results in increased backbonding to the π-accepting carbonyls.
iii) At that distance, an outer sphere mechanism seems likely; it isn't clear how something could bridge that distance, other than the peptide chain itself, which probably lacks sufficient conjugation to conduct electrons.
h) Tryptophan acts as a stepping stone between copper and rhenium. Phenylalanine, with a higher reduction potential than rhenium, does not.
i)
Exercise 8.3.1:
a) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js mol^{-1} \times 3.0 \times 10^{8} m s^{-1})}{(180 nm \times 10^{-9} m \: nm^{-1})} = 1.10 \times 10^{-18}J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 1.10 \times 10^{-18} J \times 6.02 \times 10^{23} mol^{-1} = 665000 J mol^{-1} = 665 kJ \: mol^{-1}\)
For comparison, the relatively strong and unreactive C-H bond in methane has a bond dissociation energy of only 440 kJ mol-1. (That's a thermodynamic value; to actually break the bond would cost more input of energy, to get over the kinetic energy barrier for bond cleavage.)
b) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} J \: s \: mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{(476 nm \times 10^{-9} m \: nm^{-1})} = 4.17 \times 10^{-19} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 4.42 \times 10^{-19} J \times 6.02 \times 10^{23} mol^{-1} = 251000 J \: mol^{-1} = 251 kJ \: mol^{-1}\)
c) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} J s \: mol^{-1} \times 3.0 \times 10^{8} ms^{-1})}{(645 nm \times 10^{-9} m \: nm^{-1})} = 3.08 \times 10^{-19} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 3.08 \times 10^{-19} J \times 6.02 \times 10^{23} mol^{-1} = 138000 J mol^{-1} = 138 kJ mol^{-1}\)
Exercise 8.3.2:
a) \( \lambda = \frac{1}{wavenumber} = \frac{1}{3105 cm^{-1}} = 3.22 \times 10^{-4} cm \times 0.01 m \: cm^{-1} = 3.22 \times 10^{-6} m \)
\[E = \frac{hc}{\lambda} \nonumber\]
\[E = \frac{(6.625 \times 10^{-34} J s \: mol^{-1} \times 3.0 \times 10^{8} m s^{-1})}{(3.22 \times 10^{-6}m)} = 6.17 \times 10^{-20} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 6.17 \times 10^{-20} J \times 6.02 \times 10^{23} mol^{-1} =37000 J \: mol^{-1} = 37 kJ mol^{-1}\)
b) \(\lambda = \frac{1}{wavenumber} = \frac{1}{1695 cm^{-1}} = 5.90 \times 10^{-4} cm \times 0.01 m cm^{-1} = 5.90 \times 10^{-6} m\)
\[E = \frac{hc}{\lambda} \nonumber\]
\[E = \frac{(6.625 \times 10^{-34} J \: s \: mol^{-1} \times 3.0 \times 10^{8} ms^{-1})} {(3.22 \times 10^{6} m)} = 3.37 \times 10^{-20} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 3.37 \times 10^{-20} J \times 6.02 \times 10^{23} mol^{-1} = 20000 J mol^{-1} = 20 kJ mol^{-1}\)
c) \(\lambda = \frac{1}{wavenumber} = \frac{1}{963 cm^{-1}} = 1.04 \times 10^{-3} cm \times 0.01 m \: cm^{-1} = 1.04 \times 10^{-5}\)
\[E = \frac{hc}{\lambda} \nonumber\]
\[E = \frac{(6.625 \times 10^{-34} J s mol^{-1} \times 3.0 \times 10^{8} m s^{-1})}{(1.04 \times 10^{-5} m )} = 1.91 \times 10^{-20} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 1.91 \times 10^{-20} J \times 6.02 \times 10^{23} mol^{-1} = 11500 J mol^{-1} = 11.5 kJ mol^{-1}\)
Exercise 8.3.3:
a)
b) Ru(bpy)32+ would be a terrible reducing agent. The reduction potential of Ru(bpy)33+ is very high. That means Ru(bpy)32+ would not give up an electron very easily.
c) \(\Delta G = -n F E^{0}\)
\[\Delta G = -1 \times 97485 J V^{-1}mol^{-1} \times 1.26 V = -123 kJ mol^{-1} \nonumber\]
d) It absorbs in the blue part of the spectrum and appears orange.
e) It absorbs very strongly, so probably not d-d. It is probably MLCT, from the ruthenium to the π* in the bpy ligand
f) \(E = \frac {hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 3.0 \times 10^{8} m s^{-1})}{(450 nm \times 10^{-9} m \: nm^{-1})} = 4.42 \times 10^{-19} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 4.42 \times 10^{-19} J \times 6.02 \times 10^{23} mol^{-1} = 266000 J mol^{-1} = 266 kJ mol^{-1}\)
g) Ru2+ would be low spin d6, a singlet ground state. The excited state will also be a singlet state.
h) 615 nm is in the orange region of the spectrum. This is light given off by the complex as it relaxes, so it is the colour we see.
i) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.625 \times 10^{-34} Js mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{(615 nm \times 10^{-9} m \: nm^{-1})} = 3.23 \times 10^{-19} J \nonumber\]
That's for one molecule. On a per mole basis, \(E = 3.23 \times 10^{-19} J \times 6.02 \times 10^{23} mol^{-1} = 195000 J \: mol^{-1} = 195 kJ \: mol^{-1}\)
j) Stokes shift \( =615 nm - 450 nm = 165nm\)
k) \(\Delta E = E_{1} - E_{2} = 266 - 195 kJ \: mol^{-1} = 71 kJ \: mol^{-1}\)
However, it would not be lost all at once, but in small increments equivalent to the differences between vibrational states.
l) If we were to reduce Ru(bpy)33+ directly into an excited state, we would arrive at a state much higher in energy than the ground state. That reduction would be harder to accomplish. In this case, the ending state would be 195 kJ mol-1 higher than Ru(bpy)32+.
\[\Delta G = 195 - 123 kJ \: mol^{-1} = 72 kJ \: mol^{-1} \nonumber\]
\[E^{0} = \frac{- \Delta G}{nF} = -\frac{(72 kJ \: mol^{-1} \times 1000 kJ \: J^{-1})}{(1 \times 96485 J: V^{-1} mol^{-1})} = -0.75V \nonumber\]
m) The oxidation of Ru(bpy)32+* would be very favorable compared to the oxidation of Ru(bpy)32+. The former is a much better reducing agent.
Exercise 8.5.1:
The longer the wavelength, the lower the energy. Photons of wavelength longer than 240 nm would not have enough energy to overcome the barrier for the dioxygen-cleaving reaction.
Exercise 8.5.2:
According to the Planck-Einstein relation:
\[E = h \nu \nonumber\]
or, since \(V = \frac{c}{\lambda}\)
\[E = \frac{hc}{\lambda} \nonumber\]
in which h = Planck's constant = 6.625 x 10-34 Js,
c = speed of light = 3.0 x 108 m/s,
ν = frequency,
λ = wavelength.
a) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.525 \times 10^{-34} Js)(3.0 \times 10^{8} m/s)}{(200 nm)(10^{-9} m/nm)} \nonumber\]
\[E = 9.03 \times 10^{-19} J \nonumber\]
b) \(E = \frac{hc}{\lambda}\)
\[E = \frac{(6.525 \times 10^{-34} Js)(3.0 \times 10^{8} m/s)}{(325nm)(10^{-9} m/nm)} \nonumber\]
\[E = 6.12 \times 10^{-19}J \nonumber\]
Exercise 8.5.3:
Remember, the mole is the conversion unit from the molecular scale to the macroscopic scale.
a) \(E = (8.28 \times 10^{-19} J/photon)(6.02 \times 10^{23} photons/mol)\)
\[E = 543770 \frac{J}{mol} \nonumber\]
\[E = 544 \frac{kJ}{mol} \nonumber\]
b)
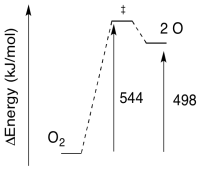
Exercise 8.5.4:
a) \(E = (6.12 \times 10^{-19} J/photon)(6.02 \times 10^{23} photons/mol)\)
\[E = 368146 \frac{J}{mol} \nonumber\]
\[E = 368 \frac{kJ}{mol} \nonumber\]
b)
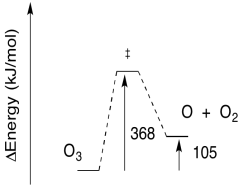
Exercise 8.5.5:
The reactions must take the same pathway, and go over the same barrier, forward and back.
a) The reverse barrier: \(E = 544-498 \frac{kJ}{mol}\)
\[E = 46 \frac{kJ}{mol} \nonumber\]
b) The reverse barrier: \(E = 368 - 105 \frac{kJ}{mol}\)
\[E = 263 \frac{kJ}{mol} \nonumber\]
Exercise 8.6.1:
- The original PDI has an absorption maximum at just under 500 nm. It absorbs blue-green, so it would be expected to appear red-orange.
- The longest wavelength absorbed is approximately 625 nm.
- \(E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{8} m s^{-1})}{625 \times 10^{-9} m} = 3.18 \times 10^{-19} J \)
That's the energy of a photon. A mole of photons would have energy multiplied by Avogadro's number, NA.
\[E = 3.18 \times 10^{-19} J \times NA = 3.18 \times 10^{-19} \times 6.02 \times 10^{23} mol^{-1} = 1.91 \times 10^{5} J \: mol^{-1} = 191 kJ mol^{-1} \nonumber\]
d) If we approximate \(E = \Delta G\), and given that \(\Delta G = -NFE^{0}\)
Then for this single-electron excitation, \(E^{0} = \frac{- \Delta G}{nF} = \frac{-1.91 \times 10^{5} J \: mol^{-1}}{(1 \times 96485 J \: V^{-1} mol^{-1})} = -1.97 V\)
e)
f) Given the structure of PDI, the transition is probably π --> π*.
g) The longest wavelength absorbed shifts toward the red, to about 700 nm, after dipping in acid. The energy of the transition is lowered to
\[E = \frac{hc}{\lambda} = \frac{(6.625 \times 10^{-34} Js \: mol^{-1} \times 3.0 \times 10^{8} m \: s^{-1})}{300 \times 10^{-9} m} = 2.84 \times 10^{-19} J \nonumber\]
\[E = 2.84 \times 10^{-19} J \times NA = 3.18 \times 10^{-19} \times 6.02 \times 10^{23} mol^{-1} = 1.71 \times 10^{5} J \: mol^{-1} = 171 kJ \: mol^{-1} \nonumber\]
h) These very flat molecules can probably stack very tightly together. The distance between the π electrons on one molecule and the π* orbital on a neighbouring molecule is very small. An intermolecular transition is possible.
i) What happens when the film is dipped in acid? It gets protonated. The anionic phosphate groups would become neutralized. The molecules would be able to stack even more closely together, lowering the energy required to excite an electron from one molecule to the other.
j) The onset of the reduction wave appears to be about -0.40 V, as shown by the peak in the cyclic voltamogram.
k)
l)
m) \(E^{0}_{(_{vs}Ag+/AgCl)} = E^{0}_{(_{vs}NHE)} + 0.20 V\) (i.e. the positive reduction potential of Ag+ vs. NHE indicates an electron is
i) \(E^{0}_{(_{vs} Ag+/AgCl)} = -0.10V + 0.20V = + 0.10 V\)
ii) \(E^{0}_{(_{vs}Ag+/AgCl)} = + 1.23 V + 0.20 V = + 1.43V\)
iii) \(E^{0}_{(_{vs}Ag+/AgCl)} = +0.83V + 0.20V = + 1.03V\)
n) The excited state can be reduced by placing an electron in the hole vacated by the excited electron. This level is 1.97 V below the conductance band in energy, which has a reduction potential of -0.40 V (its potential is 1.97 V more positive than the conductance band).
Thus, \(-0.40V + 1.97V = + 1.57V\).
o)
p)
q) The phosphates probably coordinate to the cobalt oxide, forming a bridge for electron transfer.
Exercise 8.6.2:
- \(\ce{Ag^{+}_{(aq)} + NO_{3}^{-}_{(aq)} + Bu_{4}N^{+}_{(aq)} + Br^{-}_{(aq)} -> AgBr_{(s)} + Bu_{4}N^{+}_{(aq)} + NO_{3}^{-}_{(aq)}}\)
- They absorb in the violet-blue range and would appear yellow-orange.
- A nanometer is 10-9 m, whereas a picometer is 10-12 m. A picoparticle is 1,000 times smaller than a nanoparticle.
- They absorb across the visible spectrum and appear black.


