8.6: Applications of Photochemistry- Photoredox Catalysis
- Page ID
- 190057
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)There are lots of ways that photochemistry can be harnessed to do useful things. Solar power is an obvious example: sunlight is used to excite an electron in a solar panel, leading to generation of electricity. That kind of power can potentially have a broad impact on other aspects of the energy industry. For example, a number of researchers have been trying to use sunlight as an energy source to make hydrogen from water.
Photoredox catalysis is the application of photochemistry to carry out redox reactions catalytically. For example, if sunlight were absorbed by a material such as a semiconductor, resulting in excitation of an electron, the resulting species may have the energy to reduce the protons in water to dihydrogen. If the semiconductor could be regenerated with a reducing agent, the process would be catalytic.
Perhaps the most powerful aspect of photoexcitation is that it results in both a powerful oxidant and a powerful reductant. Excitation of an electron results in electron/hole pair separation. After excitation, the electron is in a higher energy level, and it leaves behind a "hole", where the electron used to be.
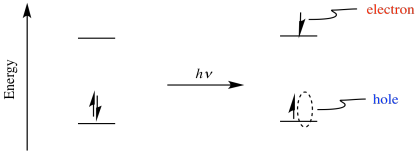
Because the electron is at a higher energy level than it used to be, donation to an acceptor is more favorable than it was before. The compound has become a better reducing agent through photoexcitation. Also, because the hole is lower in energy than the LUMO of the ground state, it will more easily accept and electron from a donor. That means the compound has also become a better oxidising agent through photoexcitation.

We can estimate how much the reducing or oxidizing power of a compound changes upon excitation by a photon. For example, the reduction potential depends upon the relative energy level of the orbital into which an electron would be donated. Upon photoexcitation, that energy level changes. It goes from the ground state LUMO to the level of the hole introduced where an electron used to be. The difference in energy between those two levels is the same as the energy of the photon that was absorbed.
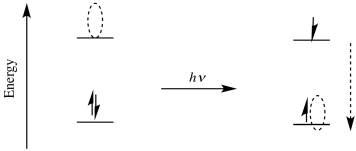
We can calculate the energy of the absorbed photon. That quantity is given by the Planck-Einstein relation:
\[E = h \nu \: or \: E= \frac{hc}{\lambda} \nonumber\]
in which E is energy, h is Planck's constant, ν is the frequency of the photon, c is the speed of light, and λ is the wavelngth of the photon.
That energy is the same as the distance between the ground state LUMO and the excited state hole. Now, that is a quantum-scale energy difference, found within a single molecule. When we talk about reduction potentials, we are discussing a macroscopic phenomenon. Reduction potentials are measured on the scale of human experience, the scale of the very large, the scale that we can easily observe. Macroscopic measurements involve vast numbers of atoms, and the convenient unit of a vast number of atoms is a mole. Remember, that's just the conversion factor between an easily measurable quantity of mass (a gram) and a quantum-scale quantity of mass (an atomic mass unit, also called an amu or a Dalton).
So we might think about how much energy it would take to get an entire mole of molecules into the excited state, which would simply require the use of Avogadro's number. Clearly this will be a much bigger amount of energy than it takes to excite a single molecule, and we would get there by multiplying by Avogadro's number.
\[E = (h \nu ) N_{A} \: or \: E = (\frac{hc}{\lambda})N_{A} \nonumber\]
in which NA = Avogadro's number.
(We could equally well be dealing with an individual atom or some other kind of compound rather than a molecule, but the argument would be the same.)
Because the excited state hole is that much lower in energy than the original LUMO, an electron falling into that hole would release that much more energy than an electron falling into the ground state LUMO. On the macroscopic scale, a mole of electrons falling into the excited state hole would release so much more energy than a mole of electrons falling into the ground state LUMO; that energy difference is the quentity that we have just calculated using Avogadro's number.

Of course, a similar argument holds for the excited state electron. It is much more likely to be donated to an acceptor after first having been excited.

We know that the free energy released when an electron falls to a lower level is related to the reduction potential. That difference is given by the relation
\[\Delta G = -nF \Delta E^{o} \nonumber\]
in which ΔG is the free energy change, n is the number of electrons transferred, F is the Faraday constant, and ΔEo is the cell reduction potential, or the difference in reduction potential between the donor and the acceptor.
Here we will make a slight approximation. The energy of the photon is roughly the difference in free energy upon electron transfer from a donor to the excited state hole compared to the ground state LUMO (although the energy calculated in the Planck-Einstein relation doesn't say anything about entropy, which is an implicit part of the free energy change).
\[E_{excitation} \sim \Delta G_{reduction} \nonumber\]
From there, it is a short step to figure out the change in reduction potential when the electron is excited.
\[\Delta E^{o}_{new} = \Delta E^{o}_{original} + \Delta E^{o}_{photo} \nonumber\]
The possibility for tremendous utility of an excited state species in catalysis arises from the fact that the excited state can be both a better reductant and a better oxidant than the ground state species. As a better oxidant, it can easily oxidize another compound; as a better reductant, it can then be reduced again, forming the original, ground state species and completing a catalytic cycle. Alternatively, it could act as a reductant first and complete the cycle by becoming reduced again; the order of the two steps does not really matter.
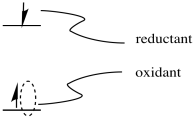
Let's think about the example of hydrogen production. Hydrogen is very appealling as a fuel because, when it burns, it provides a large amount of energy through the formation of strong O-H bonds. In addition, the product of its combustion is water, which does not pose any obvious problems as a pollutant. An economy based on hydrogen consumption is potentially more sustainable in environmental terms.
Where could we get hydrogen to drive this economy? Currently, we obtain hydrogen from coal and natural gas. In a process called steam reforming, hydrocarbon gases such as methane can be passed over a catalyst in the presence of steam, producing H2 and carbon oxygenates, mostly CO but also some CO2. A similar process can be carried out using coal instead of natural gas. The carbon monoxide is usually captured for other industrial processes, but it can also be used to make even more hydrogen via the water gas shift reaction. In the water gas shift reaction, the carbon monoxide is again treated with steam over a different catalyst, producing H2 and carbon dioxide.
Although the water gas shift reaction is exothermic, steam reforming is overall endothermic, so energy must be expended in order to produce hydrogen. That situation isn't optimal, because we end up having to spend a lot of energy in order to produce an energy source. In addition, we produce carbon dioxide, which is a greenhouse gas, the human production of which has been convincingly linked to global warming and climate change. Furthermore, coal and natural gas reserves may be plentiful right now, but the same was also once true of petroleum reserves, and although petroleum companies continue to locate and extract new deposits of petroleum, the extraction process becomes more difficult and expensive as these deposits become more and more remote or inaccessible.
Water is the most abundant source of hydrogen on earth. It would be much easier to produce hydrogen from water. People have been doing that for about 200 years, just by placing electrodes in water and applying a voltage. This is called electrolysis of water. The trouble is, the electrolysis of water requires massive amounts of electricity. Electricity production requires energy consumption. In the United States, electricity production still depends heavily on consumption of coal and natural gas, so instead of replacing our need for these commodities, we have simply removed them from sight.
Photoredox catalysis may offer a solution. By producing hydrogen from water catalytically, we take a roundabout approach that requires less energy than direct electrolysis of water. By driving the reaction photochemically, we can harness sunlight to provide that energy.
There are different possible routes that can convert protons to dihydrogen catalytically. One example occurs with coordination compounds. Some coordination compounds in low oxidation states can be protonated at the metal centre by water. Protonation of a metal centre is formally an oxidative addition. Once the proton is bound to the metal centre, it is considered a hydride ligand, so it has formally changed from H+ to H-. The two electrons to convert it to a hydride came from the metal.
Catalytic turnover results after the metal centre has been protonated twice, resulting in a pair of hydride ligands on the metal. Reductive elimination of dihydrogen returns two of the electrons to the metal centre; the other two leave with the dihydrogen. The metal still needs two more electrons from another source, because in undergoing two oxidative additions it has donated a total of four electrons to the protons.
One of the problems with this approach is that in order to make the process catalytic, the two electrons that were sent to the protons in water to make hydrogen must be replaced. Many researchers in this area have used sacrificial electron donors, compounds that can donate electrons to the catalyst to replace the ones given to the protons. Sacrificial donors could be biological cofactors such as ascorbate or succinate, or they could be simple amines.
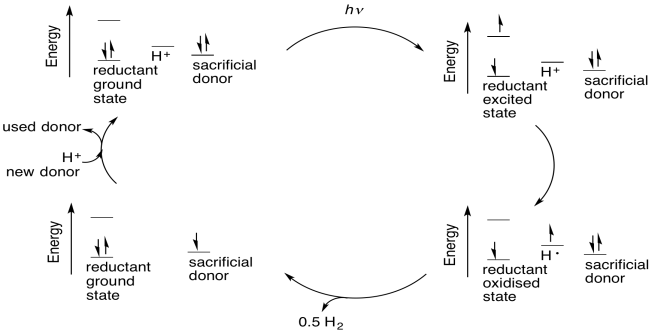
Because these donors are consumed in this process, they represent a potential inefficiency in the form of a waste side product. Some researchers hope to circumvent this problem by tying in an additional catalytic cycle that regenerates the electron donors. Others hope to bypass this problem by using the oxygen atom in water as the sacrificial donor, producing dioxygen, but doing so with a low energy cost is a challenge.
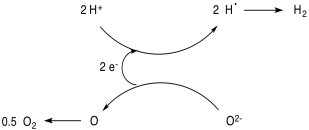
Another problem is how to drive the system photochemically. A common approach in current research efforts involves the use of semiconducting materials that can absorb sunlight (that's what solar panels are, after all). The excited state electron is passed to the catalytic component of the system, and the hole is filled by the sacrificial electron donor.
Exercise \(\PageIndex{1}\)
Researchers at Colorado State have developed a new system for photolysis of water (Finke, ACS Appl. Mater. Interfaces, 2014, ASAP).
PDI (below), a type of dye used in automobile paint, was coated onto an indium tin oxide plate. The UV-Vis spectrum was obtained and the reduction potential was measured.
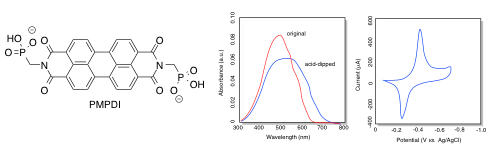
- What colour is the original PDI-coated plate?
- What is the longest wavelength absorbed?
- Translate this wavelength into energy, in kJ/mol.
- Translate this energy into a potential, in Volts.
- Show a diagram of photon absorbance to explain why this energy is a more accurate reflection of the band gap in PDI than that of other wavelengths that are absorbed.
- What type of transition is probably involved, given the structure of PDI?
\[MLCT \: d-d \: n \rightarrow \pi * \pi \rightarrow \pi * \nonumber\]
g) What happens to the energy of the transition after dipping the plate in acid?
It is thought that this transition can be intermolecular in this case:
\[2 PDI + h \nu \rightarrow PDI + \: PDI- \nonumber\]
h) Most molecules don't undergo intermolecular photonic excitation. What makes it easier in this case?
i) How is the idea of intermolecular photonic excitation consistent with the acid-dipped experiment?
j) Use the cyclic voltamogram to estimate the reduction potential of PDI vs Ag/AgCl.
Cobalt oxide was photodeposited on the PDI surface by dipping the plate in phosphate buffered (KH2PO4/ K2HPO4) cobalt nitrate solution (Co(NO3)2) and irradiating with a xenon arc lamp.
k) Show a d orbital splitting diagram for the octahedral aqueous cobalt ion before and after photon absorption.
l) Provide a mechanism for the formation of Co(IV)2O in that solution.
The following reduction potentials have been reported in the literature:
indium tin oxide: -0.10 V vs NHE
cobalt oxide: 1.23 V vs NHE
water: 0.83 V vs NHE
Now we have a problem, because some of our reduction potentials are compared to NHE; they tell us how easy it is to reduce something compared to reducing H+. Some are compared to Ag/AgCl; they tell us how easy it is to reduce something compared to reducing Ag+.
m) If the reduction potential of Ag+ is +0.20 V vs NHE, then what are the following potentials vs. Ag/AgCl?
i) indium tin oxide ii) cobalt oxide iii) water
n) Calculate the reduction potential of the excited state PDI*.
o) Fill in the appropriate energy levels for the species indicated.
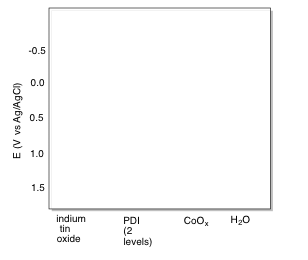
p) Add curved arrows to indicate electron flow through the system during photolytic oxygen generation.
q) Studies indicate that the system does not work if the PDI does not have phosphates attached to it. Explain why.
- Answer a
-
a) The original PDI has an absorption maximum at just under 500 nm. It absorbs blue-green, so it would be expected to appear red-orange.
- Answer b
-
b) The longest wavelength absorbed is approximately 625 nm.
- Answer c
-
c) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/625 x 10-9 m = 3.18 x 10-19 J
That's the energy of a photon. A mole of photons would have energy multiplied by Avogadro's number, NA.
E = 3.18 x 10-19 J x NA = 3.18 x 10-19 x 6.02 x 1023 mol-1 = 1.91 x 105 J mol-1 = 191 kJ mol-1
- Answer d
-
d) If we approximate E = ΔG, and given that ΔG = - nFE0
Then for this single-electron excitation, E0 = - ΔG / n F = - 1.91 x 105 J mol-1 / (1 x 96,485 J V-1 mol-1) = -1.97 V
- Answer f
-
f) Given the structure of PDI, the transition is probably π --> π*.
- Answer g
-
g) The longest wavelength absorbed shifts toward the red, to about 700 nm, after dipping in acid. The energy of the transition is lowered to
E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/700 x 10-9 m = 2.84 x 10-19 J
E = 2.84 x 10-19 J x NA = 3.18 x 10-19 x 6.02 x 1023 mol-1 = 1.71 x 105 J mol-1 = 171 kJ mol-1
- Answer h
-
h) These very flat molecules can probably stack very tightly together. The distance between the π electrons on one molecule and the π* orbital on a neighbouring molecule is very small. An intermolecular transition is possible.
- Answer i
-
i) What happens when the film is dipped in acid? It gets protonated. The anionic phosphate groups would become neutralized. The molecules would be able to stack even more closely together, lowering the energy required to excite an electron from one molecule to the other.
- Answer j
-
j) The onset of the reduction wave appears to be about -0.40 V, as shown by the peak in the cyclic voltamogram.
- Answer m
-
m) E0(vs Ag+/AgCl) = E0(vs NHE) + 0.20 V (i.e. the positive reduction potential of Ag+ vs. NHE indicates an electron is
i) E0(vs Ag+/AgCl) = - 0.10 V + 0.20 V = + 0.10 V
ii) E0(vs Ag+/AgCl) = + 1.23 V + 0.20 V = + 1.43 V
iii) E0(vs Ag+/AgCl) = + 0.83 V + 0.20 V = + 1.03 V
- Answer n
-
n) The excited state can be reduced by placing an electron in the hole vacated by the excited electron. This level is 1.97 V below the conductance band in energy, which has a reduction potential of -0.40 V (its potential is 1.97 V more positive than the conductance band).
Thus, -0.40 V + 1.97 V = + 1.57 V.
- Answer q
-
q) The phosphates probably coordinate to the cobalt oxide, forming a bridge for electron transfer.
Exercise \(\PageIndex{2}\)
Researchers in China have developed Ag-AgBr nanoparticles capable of catalysing the photochemical degradation of pollutants in sunlight. (Langmuir 2010, 26, 18723-18727)
- The AgBr nanoparticles are first formed by autoclaving AgNO3 and tetraalkylammonium bromide. Show an equation for this reaction.
- The AgBr nanoparticles absorb strongly between 250-450 nm. What colour are they?
- The structure of AgBr can be described as face centered cubic bromide with silver in the octahedral holes. Draw a unit cell.
The AgBr nanoparticles are suspended in water and exposed to sunlight for several hours until Ag picoparticles form on the surfaces of the nanoparticles.
d) Compare the size of nanoparticles to picoparticles.
e) Photoreduction of silver is believed to involve electron transfer from solvent. Show a mechanism for Ag(0) formation.
f) The Ag-AgBr nanoparticles absorb strongly from 250-850 nm. What colour are they?
In remediation assays, methyl orange is used as a stand-in for water-borne pollutants. The authors speculate that photon absorption causes electron / hole pairs that lead to reduction of O2 and oxidation of water, respectively, generating reactive oxygen species.
h) Draw an MO or band gap picture to help illustrate these two processes (water oxidation and O2 reduction).
i) Show a mechanism for radical propagation using a reactive oxygen species and methyl orange.
- Answer a
-
a) Ag+(aq) + NO3-(aq) + Bu4N+(aq) + Br -(aq) → AgBr(s) + Bu4N+ (aq) + NO3- (aq)
- Answer b
-
b) They absorb in the violet-blue range and would appear yellow-orange.
- Answer d
-
d) A nanometer is 10-9 m, whereas a picometer is 10-12 m. A picoparticle is 1,000 times smaller than a nanoparticle.
- Answer f
-
f) They absorb across the visible spectrum and appear black.


