8.1: Absorbance
- Page ID
- 190052
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Let's think first about the interaction of light with matter.
We have all seen light shine on different objects. Some objects are shiny and some are matte or dull. Some objects are different colours. Light interacts with these objects in different ways. Sometimes, light goes straight through an object, such as a window or a piece of glass.
Because chemical reactions are frequently conducted in solution, we will think about light entering a solution.
Imagine sunlight shining through a glass of soda. Maybe it is orange or grape soda; it is definitely coloured. We can see that as sunlight shines through the glass, coloured light comes out the other side. Also, less light comes out than goes in.
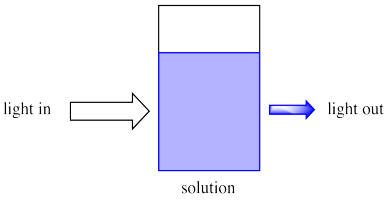
Maybe some of the light just bounces off the glass, but some of it is definitely absorbed by the soda.
So, what is the soda made of? Molecules. Some of these molecules are principally responsible for the colour of the soda. There are others, such as the ones responsible for the flavour or the fizziness of the drink, as well as plain old water molecules. The soda is a solution; it has lots of molecules (the solute) dissolved in a solvent (the water).
Light is composed of photons. As photons shine through the solution, some of the molecules catch the photons. They absorb the light. Generally, something in the molecule changes as a result. The molecule absorbs energy from the photon and is left in an excited state.
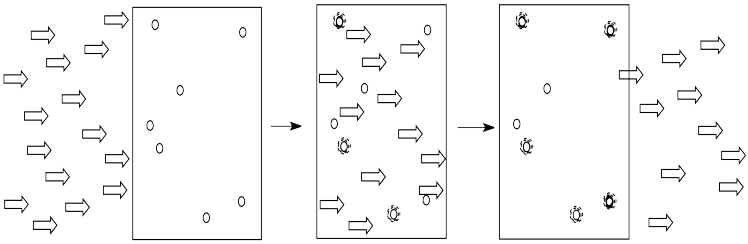
The more of these molecules there are in the solution, the more photons will be absorbed. If there are twice as many molecules in the path of the light, twice as many photons will be absorbed. If we double the concentration, we double the absorbance.
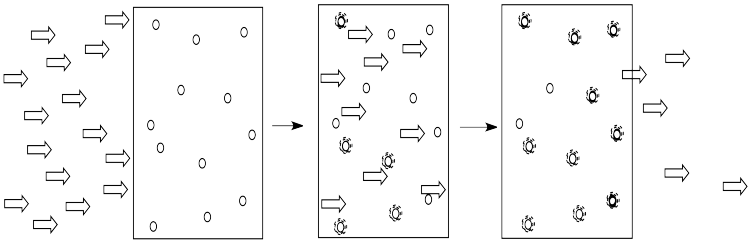
- The amount of light absorbed depends on the concentration of the solution.
Alternatively, if we kept the concentration of molecules the same, but doubled the length of the vessel through which the light traveled, it would have the same effect as doubling the concentration. Twice as much light would be absorbed.
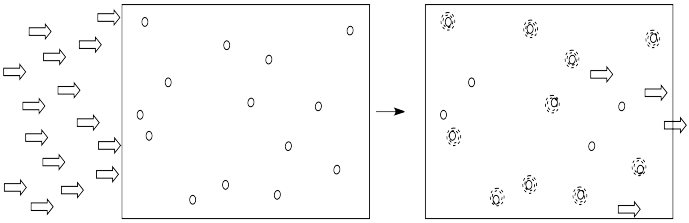
- The absorbance depends on the length of cell holding the solution.
These two factors together make up part of a mathematical relationship, called Beer's Law, describing the absorption of light by a material:
\[A = \varepsilon c l \nonumber\]
in which A = Absorbance, the percent of light absorbed; c = the concentration; l = the length of the light's path through the solution; ε = the "absorptivity" or "extinction coeficient" of the material, which is a measure of how easily it absorbs a photon that it encounters.
That last factor, ε, suggests that not all photons are absorbed easily, or that not all materials are able to absorb photons equally well. There are a couple of reasons for these differences.
Exercise \(\PageIndex{1}\)
Calculate the absorbance in the following cases.
- A sample with a molar absorptivity ε = 60 L mol-1cm-1 is diluted to a 0.01 mol L-1 solution in water and placed in a 1 cm cell.
- A sample with a molar absorptivity ε = 3,000 L mol-1cm-1 is diluted to a 3.5 x 10-5 mol L-1 solution in water and placed in a 1 cm cell.
- A sample with a molar absorptivity ε = 1.4 L mol-1cm-1 is diluted to a 0.25 mol L-1 solution in water and placed in a 0.5 cm cell.
- A sample with a molar absorptivity ε = 23,000 L mol-1cm-1 is diluted to a 2.5 x 10-6 mol L-1 solution in water and placed in a 1 cm cell.
- A sample with a molar absorptivity ε = 14,000 L mol-1cm-1 is diluted to a 0.015 mmol L-1 solution in water and placed in a 1 cm cell.
- Answer a
-
a) A = ε c l = 60 L mol-1 cm-1 x 0.01 mol L-1 x 1 cm = 0.60 = 60 %
- Answer b
-
b) A = ε c l = 3,000 L mol-1 cm-1 x 3.5 x 10-5 mol L-1 x 1 cm = 0.105 = 10.5 %
- Answer c
-
c) A = ε c l = 1.4 L mol-1 cm-1 x 0.25 mol L-1 x 0.5 cm = 0.175 = 17.5 %
- Answer d
-
d) A = ε c l = 23,000 L mol-1 cm-1 x 2.5 x 10-6 mol L-1 x 1 cm = 0.0575 = 5.75 %
- Answer e
-
e) A = ε c l = 14,000 L mol-1 cm-1 x 0.015 mmol L-1 x 1 cm = 14,000 L mol-1 cm-1 x 0.015 x 10-3 mol L-1 x 1 cm = 0.21 = 21 %
Exercise \(\PageIndex{2}\)
Calculate the extinction coefficient in the following cases.
- 30% absorbance is observed with a 0.01 mol L-1 solution in a 1 cm cell.
- 25% absorbance is observed with a 0.025 mol L-1 solution in a 1 cm cell.
- 95% absorbance is observed with a 0.00175 mol L-1 solution in a 0.5 cm cell.
- 66% absorbance is observed with a 0.025 mmol L-1 solution in a 1 cm cell.
- Answer a
-
a) ε = A /c l = 0.30 / (0.01 mol L-1 x 1 cm) = 30 L mol-1 cm-1
- Answer b
-
b) ε = A /c l = 0.25 / (0.025 mol L-1 x 1 cm) = 10 L mol-1 cm-1
- Answer c
-
c) ε = A /c l = 0.30 / (0.01 mol L-1 x 1 cm) = 543 L mol-1 cm-1
- Answer d
-
d) ε = A /c l = 0.66 / (0.025 m mol L-1 x 1 cm) = 0.66 / (0.025 x 10-3 mol L-1 x 1 cm) = 26,400 L mol-1 cm-1
Often a particular soda will absorb light of a particular colour. That means, only certain photons corresponding to a particular colour of light are absorbed by that particular soda.
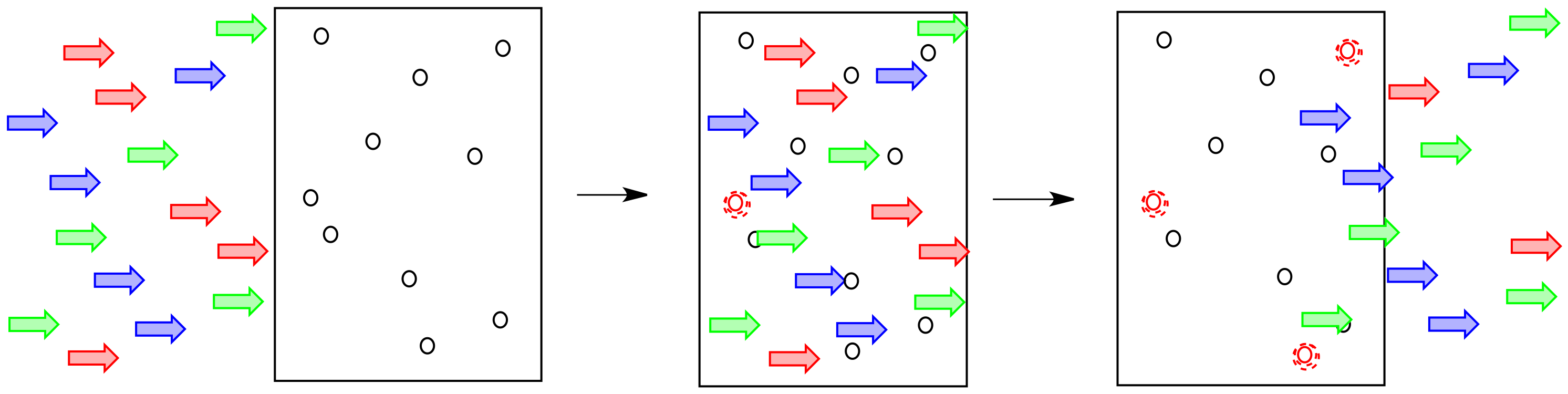
How does that affect what we see? If the red light is being absorbed by the material, it isn't coming back out again. The blue and yellow light still are, though. That means the light coming out is less red, and more yellowy-blue. We see green light emerging from the glass.
A "colour wheel" or "colour star" can help us keep track of the idea of complementary colours. When a colour is absorbed on one side of the star, we see mostly the colour on the opposite side of the star.
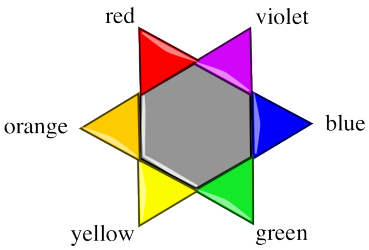
Exercise \(\PageIndex{3}\)
- What colour of photon is probably most strongly absorbed by a glass of orange soda?
- What colour of photon is most strongly absorbed by a glass of lime soda?
- What colour of photon is most strongly absorbed by a glass of blue raspberry kool-aid?
- What colour of photon is most strongly absorbed by a glass of pineapple soda?
- What colour of photon is most strongly absorbed by a glass of cherry soda?
- Answer a
-
a) blue
- Answer b
-
b) red
- Answer c
-
c) orange
- Answer d
-
d) violet
- Answer e
-
e) green
Why do certain materials absorb only certain colours of light? That has to do with the properties of photons. Photons have particle-wave duality, just like electrons. They have wave properties, including a wavelength.
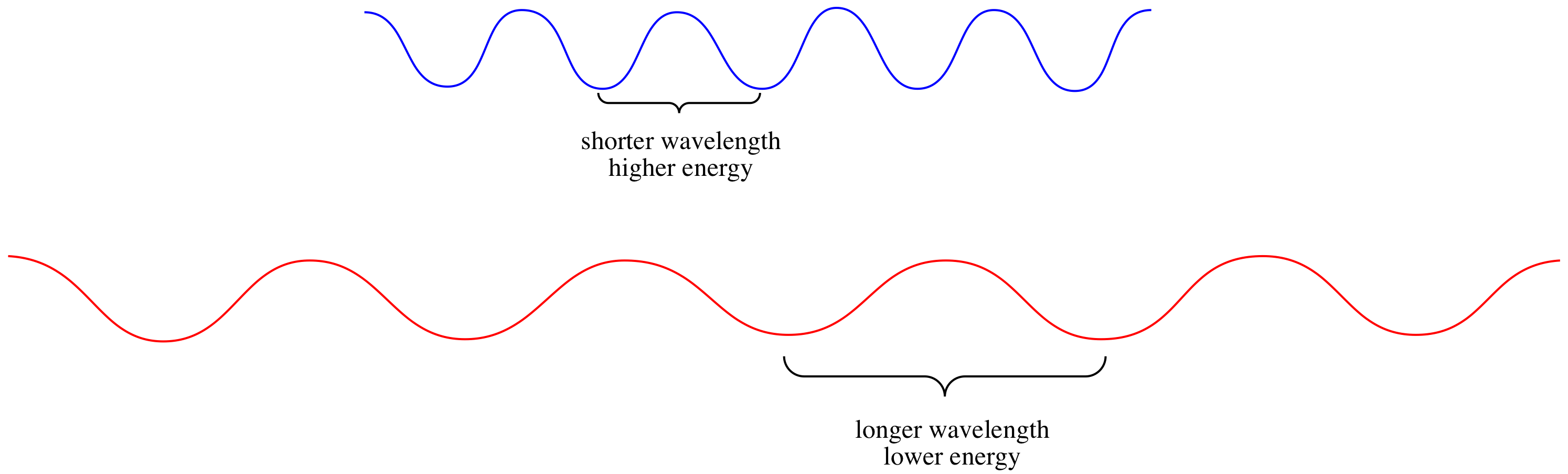
That wavelength corresponds to the energy of a photon, according to the Planck-Einstein equation:
\[E = \frac{hc}{\lambda} \nonumber\]
in which E = energy of the photon, h = Planck's constant (6.625 x 10-34 J s-1), c = speed of light (3.0 x 108 m s-1), λ = wavelength of light in m.
Alternatively, the Planck-Einstien equation can be thought of in terms of frequency of thr photon: as a photon passes through an object, how frequently does one of its "crests" or "troughs" encounter the object? How frequently does one full wavelength of the photon pass an object? That parameter is inversely proportional to the wavelength. The equation becomes:
\[E = H \nu \nonumber\]
in which ν = the frequency of the photon, in s-1.
Exercise \(\PageIndex{4}\)
- Calculate the energy of a photon with a wavelength of 1 x 10-5 m.
- Calculate the energy of a photon with a wavelength of 125 nm.
- Calculate the energy of a photon with a wavelength of 1025 nm.
- Calculate the energy of a photon with a wavelength of 450 µm.
- Calculate the energy of a photon with a wavelength of 850 Å.
- Answer a
-
a) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/1 x 10-5 m = 1.98 x 10-20 J
- Answer b
-
b) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/125 x 10-9 m = 1.59 x 10-18 J
- Answer c
-
c) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/1025 x 10-9 m = 1.94 x 10-19 J
- Answer d
-
d) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/450 x 10-6 m = 4.42 x 10-22 J
- Answer e
-
e) E = hc/λ = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/850 x 10--10 m = 2.3 x 10-18 J
Exercise \(\PageIndex{5}\)
- Calculate the wavelength of a 1.36 x 10-17 J photon.
- Calculate the wavelength of a 4.72 x 10-24 J photon.
- Calculate the wavelength of a 9.26 x 10-7 J photon.
- Answer a
-
a) λ = hc/E = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/1.46 x 10--17 J = 1.36 x 10-8 m
- Answer b
-
b) λ = hc/E = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/4.72 x 10--24 J = 4.21 x 10-2 m
- Answer c
-
c) λ = hc/E = (6.625 x 10-34 Js mol-1 x 3.0 x 108 m s-1)/9.26 x 10--17 J = 2.15 x 10-19 m
Exercise \(\PageIndex{6}\)
- Calculate the wavelength of a photon with a frequency of 6.7 x 1010 s-1.
- Calculate the wavelength of a photon with a frequency of 1500 MHz.
- Calculate the frequency of a photon with a wavelength of 9.8 x 10-10 m.
- Calculate the frequency of a photon with a wavelength of 4.3 x 10-12 m.
- Answer a
-
a) E = hν = hc/λ ; so ν = c/λ; or λ = c/ν = 3.0 x 108 m s-1/6.7 x 1010 s-1 = 4.48 x 10-3 m
- Answer b
-
b) λ = c/ν = 3.0 x 108 m s-1/1500 x 106 s-1 = 0.2 m
- Answer c
-
c) ν = c/λ = 3.0 x 108 m s-1/9.8 x 10-10 m = 3.06 x 1015 s-1
- Answer d
-
d) ν = c/λ = 3.0 x 108 m s-1/4.3 x 10-12 m = 7.0 x 1019 s-1
The visible spectrum, shown below, contains a very limited range of photon wavelengths, between about 400 and 700 nm.

The higher the frequency, the higher the energy of the photon. The longer the wavelength, the lower the energy of the photon.
As a result of this relationship, different photons have different amounts of energy, because different photons have different wavelengths.
Exercise \(\PageIndex{7}\)
Different portions of the electromagnetic spectrum interact with matter in different ways. Because of that, we can use different wavelengths of light to gain different kinds of information about a material. Calculate the amount of energy involved in the following kinds of interactions, in units of kJ/mol.
- Molecular bond rotations, measured by microwave spectroscopy. Suppose the microwave has a wavelength 1 mm long.
- Bond stretching and bending, measured by infrared spectroscopy. Suppose the IR wavelength is 1,000 nm long.
- Nuclear magnetic moments, measured by radio waves in NMR. Assume the radio wave is 1 m long.
- The excitation of an electron from one energy level to another, measured by ultraviolet and visible spectroscopy. Assume the visible light's wavelength is 500 nm long.
- Answer a
-
a) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1 mm x 10-3 m mm-1) = 1.99 x 10-22 J
That's for one molecule. On a per mole basis, E = 1.99 x 10-22 J x 6.02 x 1023 mol-1 = 120 J mol-1 = 0.12 kJ mol-1.
- Answer b
-
b) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1000 nm x 10-9 m nm-1) = 1.99 x 10-19 J
That's for one molecule. On a per mole basis, E = 1.99 x 10-19 J x 6.02 x 1023 mol-1 = 120,000 J mol-1 = 120 kJ mol-1.
- Answer c
-
c) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (1 m) = 1.99 x 10-25 J
That's for one molecule. On a per mole basis, E = 1.99 x 10-25 J x 6.02 x 1023 mol-1 = 0.120 J mol-1 = 1.2 x 10-4 kJ mol-1.
- Answer d
-
d) E = h c / λ
E = (6.625 x 10-34 J s mol-1 x 3.0 x 108 m s-1 )/ (500 nm x 10-9 m nm-1) = 3.98 x 10-19 J
That's for one molecule. On a per mole basis, E = 3.98 x 10-19 J x 6.02 x 1023 mol-1 = 239,000 J mol-1 = 239 kJ mol-1.
Exercise \(\PageIndex{8}\)
The visible spectrum ranges from photons having wavelengths from about 400 nm to 700 nm. The former is the wavelength of violet light and the latter is the wavlength of red light. Which one has higher energy: a photon of blue light or a photon of red light?
- Answer
-
Blue.
Exercise \(\PageIndex{9}\)
Ultraviolet light -- invisible to humans and with wavelengths beyond that of violet light -- is associated with damage to skin; these are the cancer-causing rays from the sun. Explain their danger in terms of their relative energy.
- Answer
-
Ultraviolet light, with a shorter wavelength than visible light, is much higher in energy and potentially more damaging.
Different materials absorb photons of different wavelengths because absorption of a photon is an absorption of energy. Something must be done with that energy. In the case of ultraviolet and visible light, the energy is of the right general magnitude to excite an electron to a higher energy level.
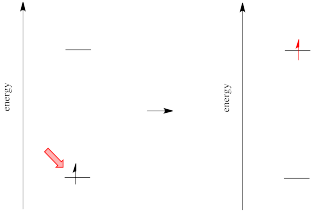
However, we know that energy is quantized. That means photons will be absorbed only if they have exactly the right amount of energy to promote an electron from its starting energy level to a higher one (producing an "excited state"). Just like Goldilocks, a photon with too much energy won't do the trick. Neither will a photon with too little. It has to be just right.
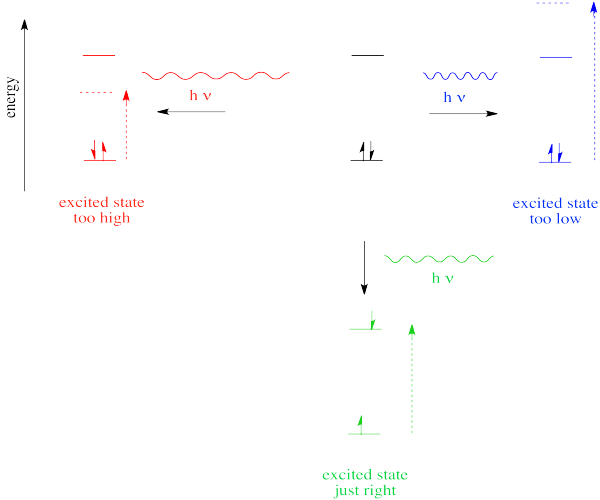
If the absorption of a UV-visible photon is coupled to the excitation of an electron, what happens when the electron falls back down to the ground state? You might expect a photon to be released.
This phenomenon was observed during the late nineteenth century, when scientists studied the "emission spectra" of metal ions. In these studies, the metal ions would be heated in a flame, producing characteristic colours. In that event, the electron would be thermally promoted to a higher energy level, and when it relaxed, a photon would be emitted corresponding to the energy of relaxation.

By passing this light through a prism or grating, scientists could separate the observed colour into separate lines of different wavelengths. This evidence led directly to the idea of Niels Bohr and others that atoms had electrons in different energy levels, which is part of our view of electronic structure today.


