1.14: Solutions to Selected Problems

Exercise 1.1.1:

a) Ag⁺ b) Ni²⁺ c) Mn⁷⁺ d) Cr⁶⁺ e) Cu³⁺ f) Fe³⁺ g)Os⁸⁺ h) Re⁵⁺

Exercise 1.1.3:

a) Pb²⁺ & S^2- b) Sn⁴⁺ & 2 O^2- c) Hg²⁺ & S^2- d) Fe⁴⁺ & 2 S^2- e) 2 Fe³⁺ & 3 O^2- f) 2 Fe³⁺ & 1 Fe²⁺ & 4 O^2-

Exercise 1.1.4:

Probably Fe²⁺, to replace Zn²⁺ ions.

Exercise 1.1.5:

a) C ²⁺ b) C⁴⁺ c) ^4- d) C⁰ e) C³⁺

Exercise 1.1.7:

a) Mg²⁺ b) Cu²⁺ c) Mn³⁺ d) Ca²⁺ e) Mn²⁺ f) Mn²⁺

Exercise 1.1.8:

a) Cu(II), Fe(II) b) Zn(II), Fe(III) c) Be(II), Al(III) d) Cu(I), Fe(III) e) Cu(II), Al(III)

Exercise 1.2.1:

1. \(\ce{Cu -> Cu^{+} + e^{-}}\)
2. \(\ce{Fe^{3+} + 3e^{-} -> Fe}\)
3. \(\ce{Mn -> Mn^{3+} + 3e^{-}}\)
4. \(\ce{Zn^{2+} + 2e^{-} -> Zn}\)
5. \(\ce{2F^{-} -> F2 + 2e^{-}}\)
6. \(\ce{H2 + 2H^{+} + 2e^{-}}\)

Exercise 1.2.2:

1. \(\ce{ Cu(I) + Fe(III) -> Cu(II) + Fe(II)}\)
2. \(\ce{Cu(I) + Ag(0) -> Cu(0) + Ag(I)}\)
3. \(\ce{3F2 + 2Fe -> 6F^{-} + 2Fe(III)}\)
4. \(\ce{2Mo^{3+} + 3Mn -> 2Mo + 3Mn^{2+}}\)

Exercise 1.2.3:

1. \(\ce{MnO2 + 2H^{+} + 2e^{-} -> Mn(OH)2}\)
2. \(\ce{2NO + 2e^{-} + 2H^{+} -> N2O + H2O}\)
3. \(\ce{HPO3^{2-} + 2e^{-} + 3H^{+} -> H2PO2^{-} + H2O}\)
4. \(\ce{Sn(OH)6^{2-} + 2e^{-} + 3H^{+} -> HSnO2^{-} + 4H2O}\)

Exercise 1.2.4:

a) yes b) no c) yes d) no e) yes f) yes g) yes h) no

Exercise 1.2.5:

1. \(E_{rxn} = -0.153V-0.33V=-0.483V\)
2. No.

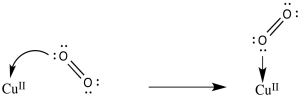
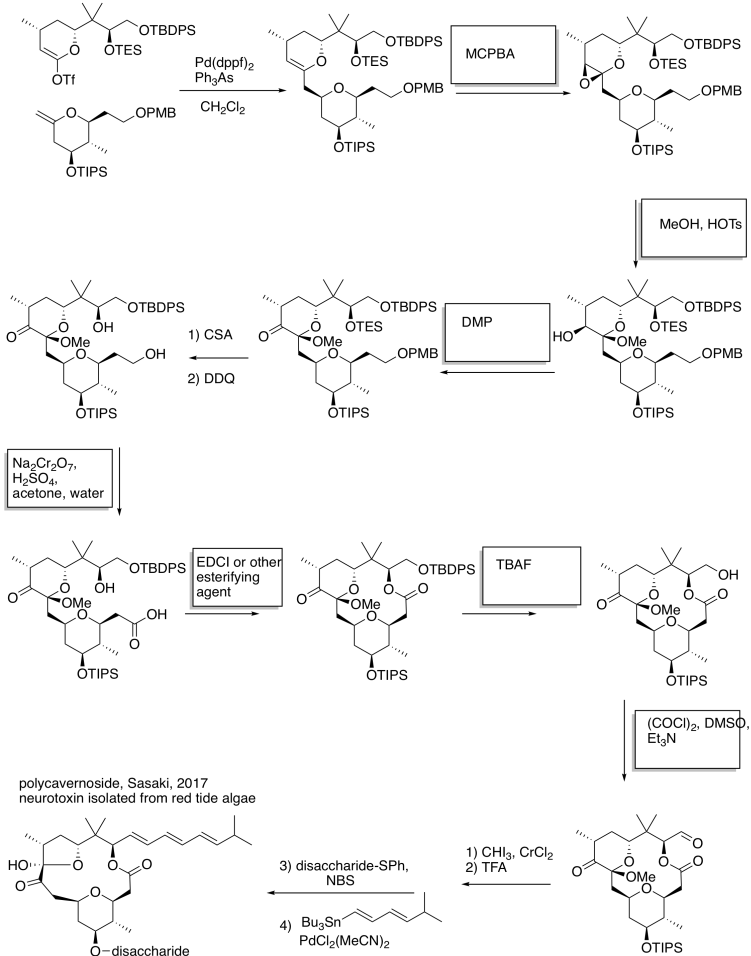
d) The O₂ is activated as an electrophile. Addition of an electron may become easier.

e) The reduction potential is 0.2 V more positive when the resulting superoxide ion is stabilised by binding a proton. A similar shift could occur when coordinated to copper.

f)

g) The two aspartate ions would make the copper complex less cationic. That may make it easier to remove an electron from the copper complex.

Exercise 1.2.6:

1. \(\ce{Fe^{2+} + ClO2 -> Fe^{3+} + ClO2^{-}}\)
2. \(E_{rxn} = 0.95V - 0.77V = 0.18V\)
3. yes.

e) ClO₂ has an unpaired electron. ClO₂^- has electrons paired

f) It could be inner sphere: the oxygen in the ClO₂ could coordinate to the iron.

g) The mixture quickly forms (H₂O)₅Fe(ClO₂)²⁺ via inner sphere electron transfer.

Exercise 1.3.1:

MnO₄^- : \(4 \times O^{2-} \: (=8^{-}) + Mn^{7+} = 1^{-}\) overall

MnO₂ : \(2 \times O^{2-} \: (=4^{-}) + Mn^{4+} =\) neutral overall

difference = 3 e^-

Exercise 1.3.2:

a) SO₄^2- : \(4 \times O^{2-} \: (=8^{-}) + S^{6+} = 2^{-}\) overall

S₂O₈^2- : \(8 \times O^{2-} \: (=16^{-}) + 2 \times S^{7+} \: (=14^{+}) = 2^{-}\) overall

difference = 1 e^- per S, or 2 e^- overall

\[\ce{S2O8^{2-} + 2e^{-} -> 2SO4^{2-}} \nonumber\]

b) HPO₃^2- : \(3 \times O^{2-} \: (=6^{-}) + H^{+} + P^{3+} = 2^{-}\) overall

P : P(0)

difference = 3 e^-

\[\ce{HPO3^{2-} + 3e^{-} + 5H^{+} -> P + 3H2O} \nonumber\]

c) Ti₂O₃ : \(3 \times O^{2-} \: (=6^{-}) + 2 \times Ti^{3+} \: (= 6^{+})\) = neutral overall

TiO : O^2- + Ti²⁺ = neutral overall

difference = 1 e^- per Ti, or 2 e^- overall

\[\ce{Ti2O3 + 2e^{-} + 2H^{+} -> 2TiO + H2O} \nonumber\]

d) N₂ : N(0)

NH₂OH : \(O^{2-} + 3 \times H^{+} \: (=3^{+}) + N^{-}\) = neutral overall

difference = 1 e^- per N, or 2 e^- overall

\[\ce{N2 + 2e^{-} + 2H^{+} + 2H2O -> 2NH2OH} \nonumber\]

Exercise 1.3.3:

Lithium is an alkali metal, in the first column of the periodic table. It has a relatively low ionization energy because it has a noble gas configuration as a cation. That noble gas configuration is stable because of the relatively large number of nuclear protons and a relatively short distance between the nucleus and the outermost shell of electrons. In lithium metal, the outermost electron is relatively far from the nucleus and so it is at a relatively high energy, and easily lost.

Exercise 1.3.4

Fluorine is a halogen, with a relatively high electron affinity. It easily gains an electron to get to a noble gas configuration as a fluoride anion. That noble gas configuration is stable because of the relatively large number of nuclear protons and a relatively short distance between the nucleus and the outermost shell of electrons.

Exercise 1.3.5:

From most easily oxidized to least easily oxidized: Li > Al > Fe > Cu > Au

Exercise 1.3.6:

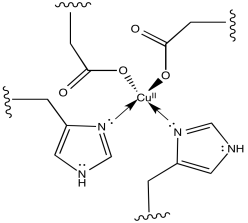
1. \(E^{0} = + 0.796 (\frac{Ag^{+}}{Ag}) - 1.83 (\frac{Au}{Au^{+}}) = -1.034V\) (no forward reaction)
2. \(E^{0} = -0.44 (\frac{Fe^{2+}}{Fe}) + 0.762 (\frac{Zn}{Zn^{2+}}) = +0.0322V\) (forward reaction)
3. \(E^{0} = +0.52 (\frac{Cu^{+}}{Cu}) + 3.04(\frac{Li}{Li^{+}}) = +3.56V\) (forward reaction)
4. \(E^{0} = +0.77 (\frac{Fe^{3+}}{Fe^{3+}}) - 0.796(\frac{Ag}{Ag^{+}}) = -0.026V\) (no forward reaction)

Exercise 1.3.7:

When the table of standard reduction potentials is displayed with the most negative value at the top and the most positive value at the bottom, any given half-reaction will go forward if it is coupled with the reverse of a half-reaction that lies above it in the table. The opposite is not the case; no half reaction will go forward if it is coupled with the reverse of a half-reaction below it in the table.

Exercise 1.4.1:

a)

b)

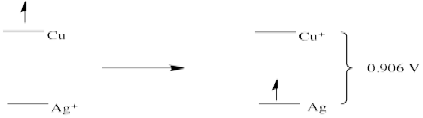
c)

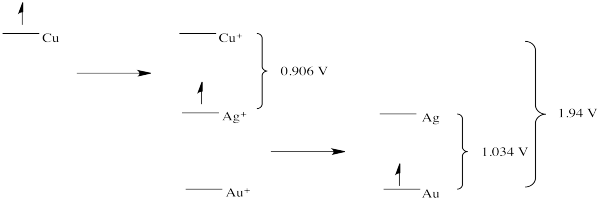
Exercise 1.4.2:

1. \(\ce{2Li + F2 -> 2Li^{+} + 2F^{-}}\)
2. E^o = +5.91 V
3. Things look pretty grim.

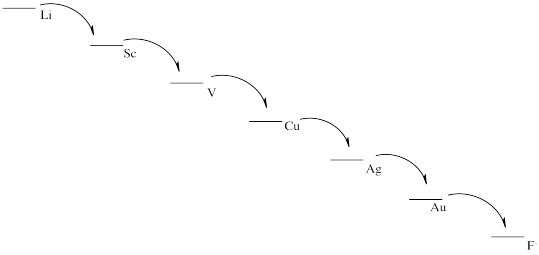
e) This scheme would result in the release of a small amount of energy at each stage. Each step could be harnessed to perform a task more efficiently, with less heat loss.

Exercise 1.4.3:

Exercise 1.4.4:

Exercise 1.4.5:

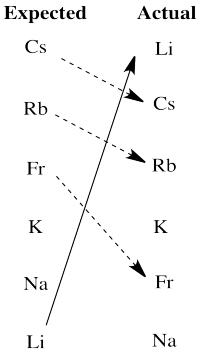
There are really two significant departures from expectation here. Lithium is much more active than expected based on electronegativity. The larger alkali metals, cesium, rubidium and francium, are all less active than expected on that basis.

We will see that another factor the influences activity in redox is the stability of ions in aqueous solution. Lithium cation is a small ion; water molecules bind very strongly to the ion because the electrons get relatively close to lithium's nucleus. That strong binding stabilizes this ion especially, tipping the malance of the reaction more strongly towards oxidation of lithium. The larger alkali metal ions are not nearly as stabilized by water ligands in aqueous solution, so the balance of their reactions does not tilt as strongly towards aqueous ions.

Exercise 1.5.1:

Li⁺/Li: \(E^{0} = -3.04V\); \(\Delta H_{vap} = 147 \frac{kJ}{mol}\); \(IE = 520 \frac{kJ}{mol}\); \(\Delta H_{h} = -520 \frac{kJ}{mol}\)

Na⁺/Na: \(E^{0} = -2.71V\); \(\Delta H_{vap} = 97 \frac{kJ}{mol}\); \(IE = 495 \frac{kJ}{mol}\); \(\Delta H_{h} = -406 \frac{kJ}{mol}\)

K⁺/K: \(E^{0} = -2.931V\); \(\Delta H_{vap} = 77 \frac{kJ}{mol}\); \(IE= 419 \frac{kJ}{mol}\); \(\Delta H_{h} = -320 \frac{kJ}{mol}\)

Potassium should be the easiest of the three to oxidize. It is easier to oxidize than sodium. However, lithium's high heat of hydration reverses the trend and tips the balance of reaction in favor of ion formation.

Exercise 1.5.2:

Cu²⁺/Cu: \(E^{0} = + 0.340V\); \(\Delta H_{vap} = 300 \frac{kJ}{mol}\); \(IE = 745 \frac{kJ}{mol} \& 1958 \frac{kJ}{mol}\); \(\Delta H_{h} = -2099 \frac{kJ}{mol}\)

Ni²⁺/Ni: \(E^{0} = -0.25V\); \(\Delta H_{vap} = 377 \frac{kJ}{mol}\); \(IE = 737 \frac{kJ}{mol} \& 1753 \frac{kJ}{mol}\); \(\Delta H_{h} = -2096 \frac{kJ}{mol}\)

Zn²⁺/Zn: \(E^{0} = -0.7618V\); \(\Delta H_{vap} = 123 \frac{kJ}{mol}\); \(IE = 906 \frac{kJ}{mol} \& 1733 \frac{kJ}{mol}\); \(\Delta H_{h} = -2047 \frac{kJ}{mol}\)

In this case, zinc may be considered the outlier. Copper should be easier to reduce than nickel based solely on electronegativity. However, zinc's very low heat of vaporization suggests that formation of the solid metal is less favored in that case, helping to tilt the balance toward zinc ion instead.

Exercise 1.5.3:

a)

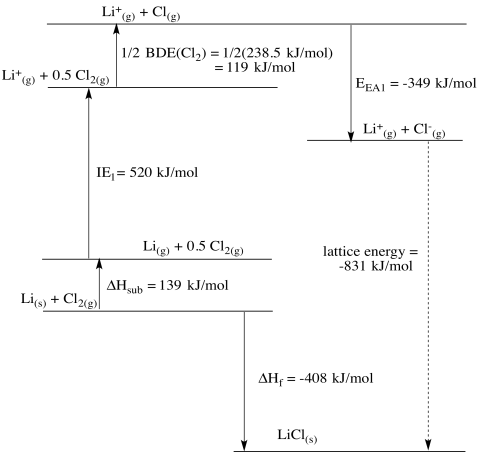
b)

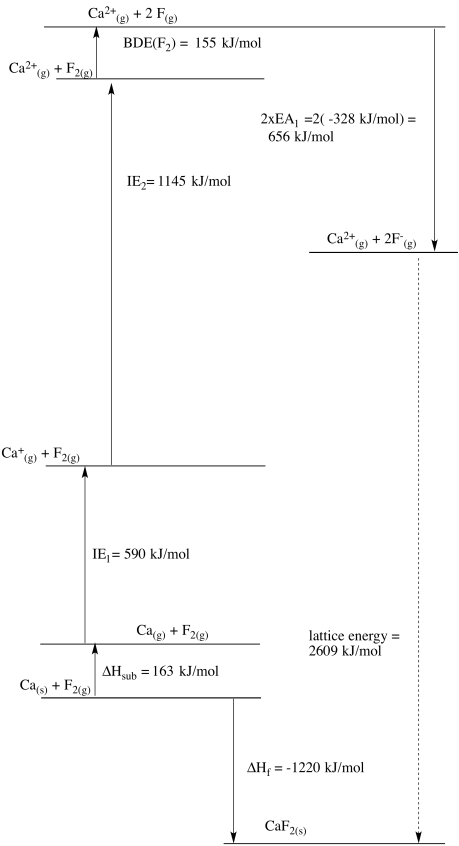
c)

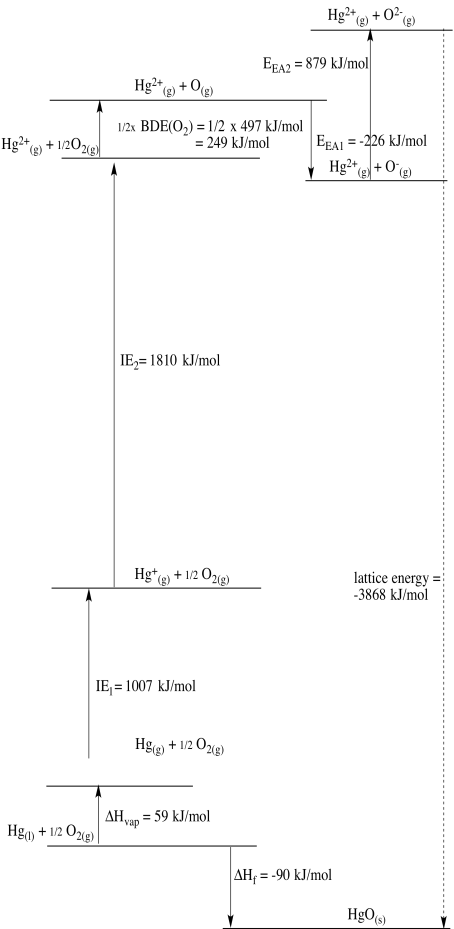
d)

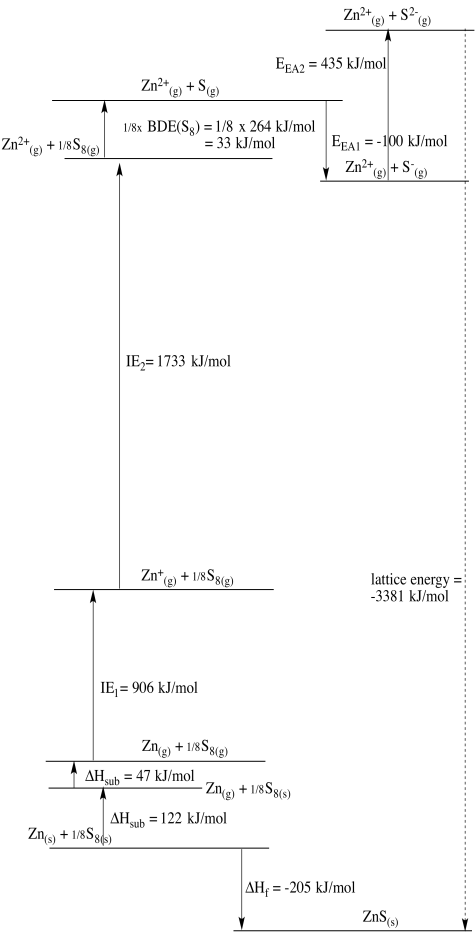
Exercise 1.6.1:

Both reduction potentials are very positive.

\[\ce{Ag^{+} + e^{-} -> Ag (s)} \: E^{0} = + 0.796V \nonumber\]

\[\ce{Au^{+} + e^{-} -> Au (s)} \: E^{0} = +1.83V \nonumber\]

That means both metals are likely to be found in the reduced state.

Exercise 1.6.2:

\[\ce{SnO (s) + 2H^{+} + 2e^{-} -> Sn (s) + H2O} \: E^{0} = -0.10V \nonumber\]

\[\ce{CO (g) + H2O -> CO2 (g) + 2H^{+} + 2e^{-}} \: E^{0} = -(-0.11V) \nonumber\]

\[\ce{SnO (s) + CO (g) -> Sn (s) + CO2 (g)} \: \Delta E^{0} = + 0.01V \nonumber\]

Exercise 1.6.3:

\[\ce{Fe3O4 (s) + 8H^{+} + 8e^{-} -> 3Fe(s) + 4H2O} \: E^{0} = + 0.085V \nonumber\]

\[\ce{CO(g) + H2O -> CO2(g) + 2H^{+} + 2e^{-}} \: E^{0} = -(-0.11V) \nonumber\]

\[\ce{Fe3O4(s) + 4CO (g) -> 3Fe (s) + 4CO2 (g)} \: \Delta E^{0} = 0.195V \nonumber\]

Exercise 1.6.4:

\[\ce{Al^{3+}_{(aq)} + 3e^{-} -> Al(s)} \: E^{0}= -1.662V \nonumber\]

\[\ce{CO(g) + H2O -> CO2(g) + 2H^{+} + 2e^{-}} \: E^{0} = -(-0.11V) \nonumber\]

\[\ce{2Al^{3+} (aq) + 3CO (g) + 3H2O -> 2Al(s) + 3CO2 (g)} \: \Delta E^{0} = -1.772V \nonumber\]

Exercise 1.6.5:

\[\ce{Al^{3+} + 3e^{-} -> Al(s)} \: E^{0} = -1.662V \nonumber\]

\[\ce{2O^{2-} -> O2(g) + 4e^{-}} \: E^{0} = -(.40V, \: estimated) \nonumber\]

\[\ce{4Al^{3+}(aq) + 6O^{2-} (aq) -> 4Al (s) + 3O2 (g)} \: \Delta E^{0} = -2.062V \nonumber\]

Even if the aluminum ions from the cryolite are reduced to Al⁰, they will be replenished by new aluminum ions from the bauxite ore.

Exercise 1.7.1:

\[\Delta G = -nFE^{0}_{cell} \nonumber\]

\[\Delta G = -2 \times 96485 \frac{J}{V \: mol} \times 1.43V \nonumber\]

\[\Delta G = -275947 \frac{J}{mol} = -276 \frac{kJ}{mol} \nonumber\]

Exercise 1.7.2:

\[\Delta G = -nFE^{0}_{cell} \nonumber\]

\[\Delta G = -2 \times 96485 \frac {J}{V \: mol} \times 1.3V \nonumber\]

\[\Delta G = -250861 \frac {J}{mol} = -251 \frac {kJ}{mol} \nonumber\]

Exercise 1.7.3:

\[\ce{Ag2O (s) + H2O + 2e^{-} -> 2 Ag (s) + 2OH^{-} (aq)} E^{0} = +0.342V \nonumber\]

\[\ce{Zn (s) -> Zn^{2+}(aq) + 2e^{-}} \: E^{0}= -(-0.762V) \nonumber\]

\[\ce{Ag2O (s) + H2O + Zn(s) -> 2Ag (s) + 2OH^{-} (aq) + Zn^{2+} (aq)} \: \Delta E^{0} = +1.104V \nonumber\]

Exercise 1.7.4:

a) Charge on complex calculated as follows:

charge on metal: 3+

charge on ligand donors (4 neutral N, 2 anionic N donors): 2-

other charges on ligand (carboxylate arm): 1-

overall: 0

b) \(\Delta GG = RT log K = RT (-pK_{a}) = -8.314 \frac{J} {K \: mol} \times 300K \times (-20.2) = 50382 \frac{J}{mol} = 50.4 \frac{kJ}{mol}\)

c) It is more difficult to add the electron to the more negatively charged anion, so the reduction potential is more negative in that case.

d) \(\Delta G = -nFE^{o} = -1 \times 96485 \frac{J}{V \: mol} \times (-0.545V) = 52583 \frac{J}{mol} = 52.6 \frac{kJ}{mol}\)

e) \(\Delta G = -nFE^{o} = -1 \times 96485 \frac{J}{V \: mol} \times (-0.575V) = 55479 \frac{J}{mol} = 55.5 \frac{kJ}{mol}\)

f)

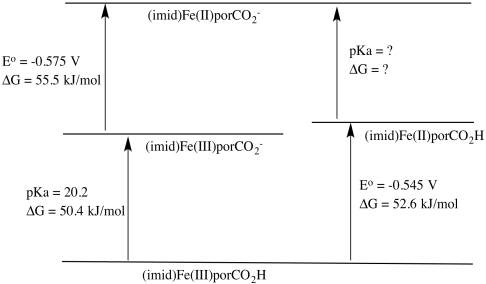
\[\Delta G_{Fe(II)CO_{2}H/CO_{2}^{-}} = 50.4 + 55.5 -52.6 \frac{kJ}{mol} = 53.3 \frac{kJ}{mol} \nonumber\]

\[\Delta G = -RT log K_{a} \nonumber\]

\[K_{a} = e^{(\frac{-\Delta G}{RT})} = e^{(\frac{-53300}{8.314 J/K mol \times 300K})} = e^{-21.4} \nonumber\]

pKa = 21.4

g) The Fe(III) complex is easier to deprotonate because it yields an anionic species, whereas the Fe(II) complex yields a dianionic species. The greater charge buildup in the latter would cost more energy.

Exercise 1.8.1:

a) \(\ce{Cu -> Cu2O}\) \(\ce{MoO2 -> Mo}\)

\[\ce{2Cu -> Cu2O}\) \(\ce{MoO2 -> Mo} \nonumber\]

\[\ce{2Cu + H2O -> Cu2O}\) \(\ce{MoO2 -> Mo + 2H2O} \nonumber\]

\[\ce{2Cu + H2O -> Cu2O + 2H^{+}}\) \(\ce{4H^{+} + MoO2 -> Mo + 2H2O} \nonumber\]

\[\ce{2Cu + H2O -> Cu2O + 2H^{+} + 2e^{-}}\) \(\ce{4e^{-} + 4H^{+} + MoO2 -> Mo + 2H2O} \nonumber\]

\[2 \times (\ce{2 Cu + H2O -> Cu2O + 2H^{+} + 2e^{-}})\) \(\ce{4e^{-} + 4H^{+} + MoO2 -> Mo + 2H2O} \nonumber\]

adding:

\[\ce{4Cu + 2H2O -> 2Cu2O + 4H^{+} + 4e^{-}} \nonumber\]

\[\ce{4e^{-} + 4H^{+} + MoO2 -> Mo + 2H2O} \nonumber\]

equals

\[\ce{4Cu + MoO2 -> 2Cu2O + Mo} \nonumber\]

b) \(\ce{NH2OH -> N2}\) \(\ce{Ag2O -> Ag}\)

\[\ce{2NH2OH -> N2}\) \(\ce{Ag2O -> 2Ag} \nonumber\]

\[\ce{2NH2OH -> N2 + 2H2O}\) \(\ce{Ag2O -> 2Ag + H2O} \nonumber\]

\[\ce{2NH2OH -> N2 + 2H2O + 2H^{+}}\) \(\ce{2H^{+} + Ag2O -> 2Ag + H2O} \nonumber\]

\[\ce{2NH2OH -> N2 + 2H2O + 2H^{+} + 2e^{-}}\) \(\ce{2H^{+} + Ag2O + 2e^{-} -> 2Ag + H2O} \nonumber\]

adding:

\[\ce{2NH2OH -> N2 + 2H2O + 2H^{+} + 2e^{-}} \nonumber\]

\[\ce{2H^{+} + Ag2O + 2e^{-} -> 2Ag + H2O} \nonumber\]

equals

\[\ce{2NH2OH + Ag2O -> N2 + 2Ag + 3H2O} \nonumber\]

c) \(\ce{Fe3O4 -> Fe}\) \(\ce{CO -> CO2}\)

\[\ce{Fe3O4 -> 3Fe}\) \(\ce{CO -> CO2} \nonumber\]

\[\ce{Fe3O4 -> 3Fe + 4H2O}\) \(\ce{H2O + CO -> CO2} \nonumber\]

\[\ce{8H^{+} + Fe3O4 -> 3Fe + 4H2O}\) \(\ce{H2O + CO -> CO2 + 2H^{+}} \nonumber\]

\[\ce{8e^{-} + 8H^{+} + Fe3O4 -> 3Fe + 4H2O}\) \(\ce{H2O + CO -> CO2 + 2H^{+} + 2e^{-}} \nonumber\]

\[\ce{8e^{-} + 8H^{+} + Fe3O4 -> 3Fe + 4H2O}\) \(4 \times \ce{(H2O + CO -> CO2 + 2H^{+} + 2e^{-})} \nonumber\]

adding:

\[\ce{8e^{-} + 8H^{+} + Fe3O4 -> 3Fe + 4H2O} \nonumber\]

\[\ce{4H2O + 4CO -> 4CO2 + 8H^{+} + 8e^{-}} \nonumber\]

equals

\[\ce{Fe3O4 + 4CO -> 3Fe + 4CO2} \nonumber\]

d) \(\ce{I2 -> IO3^{-}}\) \(\ce{MnO4^{-} -> MnO2}\)

\[\ce{I2 -> 2IO3^{-}}\) \(\ce{MnO4^{-} -> MnO2} \nonumber\]

\[\ce{6H2O + I2 -> 2IO3^{-}}\) \(\ce{MnO4^{-} -> MnO2 + 2H2O} \nonumber\]

\[\ce{6H2O + I2 -> 2IO3^{-} + 12H^{+}}\) \(\ce{4H^{+} + MnO4^{-} -> MnO2 + 2H2O} \nonumber\]

\[\ce{6H2O + I2 -> 2IO3^{-} + 12H^{+} + 10e^{-}}\) \(\ce{3e^{-} + 4H^{+} + MnO4^{-} -> MnO2 + 2H2O} \nonumber\]

\[3 \times (\ce{6H2O + I2 -> 2IO3^{-} + 12H^{+} + 10e^{-}})\) \(10 \times (\ce{3e^{-} + 4H^{+} + MnO4^{-} -> MnO2 + 2H2O}) \nonumber\]

adding

\[\ce{18H2O + 3I2 -> 6IO3^{-} + 36H^{+} + 30e^{-}} \nonumber\]

\[\ce{30e^{-} + 40H^{+} + 10 MnO4^{-} -> 10MnO2 + 20H2O} \nonumber\]

equals

\[\ce{3I2 + 4H^{+} + 10MnO4^{-} -> 6IO3^{-} + 10 MnO2 + 2H2O} \nonumber\]

e) \(\ce{H3Mo7O24 -> Mo}\) \(\ce{S2O3^{2-} -> SO3^{2-}}\)

\[\ce{H3Mo7O24 -> 7Mo}\) \(\ce{S2Oe^{2-} -> 2SO3^{2-}} \nonumber\]

\[\ce{H3Mo7O24 -> 7Mo + 24H2O}\) \(\ce{3H2O + S2O3^{2-} -> 2So3^{2-}} \nonumber\]

\[\ce{45H^{+} + H3Mo7O24 -> 7MO + 24 H2O}\) \(\ce{3H2O + S2O3^{2-} -> 2SO3^{2-} + 6H^{+}} \nonumber\]

\[\ce{45e^{-} + 45 H^{+} + H3Mo7O24 -> 7Mo + 24 H2O}\) \(\ce{3H2O + S2O3^{2-} -> 2SO3^{2-} + 6H^{+} + 4e^{-}} \nonumber\]

\[4 \times (\ce{45 e^{-} + 21H^{+} + H3Mo7O24 -> 7Mo + 24 H2O})\) \( 45 \times (\ce{3H2O + S2O3^{2-} -> 2SO3^{2-} + 6H^{+} + 4e^{-}}) \nonumber\]

adding:

\[\ce{180e^{-} + 180H^{+} + 4H3Mo7O24 -> 28 Mo + 96 H2O} \nonumber\]

\[\ce{135 H2O + 45 S2O3^{2-} -> 90 SO3^{2-} + 270 H^{+} + 180 e^{-}} \nonumber\]

equals

\[\ce{4H3Mo7O24 + 45 S2O3^{2-} + 39 H2O-> 28 Mo + 90 SO3^{2-} + 90H^{+}} \nonumber\]

checking:

\[\ce{28Mo -> 28Mo}; \: \ce{90S -> 90S}; \: \ce{90H -> 90H}; \: \ce{270O -> 270O} \nonumber\]

Exercise 1.8.2:

a) \(\ce{Fe(OH)2 -> Fe2O3}\) \(\ce{N2H4 -> NH4^{+}}\)

\[\ce{2Fe(OH)2 -> Fe2O3}\) \(\ce{N2H4 -> 2NH4^{+}} \nonumber\]

\[\ce{2Fe(OH)2 -> Fe2O3 + H2O}\) \(\ce{N2H4 -> 2NH4^{+}} \nonumber\]

\[\ce{2Fe(OH)2 -> Fe2O3 + H2O + 2H^{+}}\) \(\ce{4H^{+} + N2H4 -> 2NH4^{+}} \nonumber\]

\[\ce{2Fe(OH)2 -> Fe2O3 + H2O + 2H^{+} + 2e^{-}}\) \(\ce{2e^{-} + 4H^{+} + N2H4 -> 2NH4^{+}} \nonumber\]

adding:

\[\ce{2Fe(OH)2 -> Fe2O3 + H2O + 2H^{+} + 2e^{-}} \nonumber\]

\[\ce{2e^{-} + 4H^{+} + N2H4 -> 2NH4^{+}} \nonumber\]

equals:

\[\ce{2Fe(OH)2 + 2H^{+} + N2H4 -> Fe2O3 + H2O + 2NH4^{+}} \nonumber\]

in basic conditions:

\[\ce{2Fe(OH)2 + 2H^{+} + 2 OH^{-} + N2H4 -> Fe2O3 + H2O + 2NH4^{+} + 2OH^{-}} \nonumber\]

\[\ce{2Fe(OH)2 + 2H2O + N2H4 -> Fe2O3 + H2O + 2NH4^{+} + 2OH^{-}} \nonumber\]

\[\ce{2Fe(OH)2 + H2O + N2H4 -> Fe2O3 + 2NH4^{+} + 2OH^{-}} \nonumber\]

b) \(\ce{MnO4^{-} -> HMnO4^{-}}\) \(\ce{V^{3+} -> VO^{2+}}\)

\[\ce{MnO4^{-} -> HMnO4^{-}}\) \(\ce{V^{3+} + H2O -> VO^{2+}} \nonumber\]

\[\ce{H^{+} + MnO4^{-} -> HMnO4^{-}}\) \(\ce{V^{3+} + H2O -> VO^{2+} + 2H^{+}} \nonumber\]

\[\ce{e^{-} + H^{+} + MnO4^{-} -> HMnO4^{-}}\) \(\ce{V^{3+} + H2O -> VO^{2+} + 2H^{+} + e^{-}} \nonumber\]

adding:

\[\ce{e^{-} + H^{+} + MnO4^{-} -> HMnO4^{-}} \nonumber\]

\[\ce{V^{3+} + H2O -> VO^{2+} + 2H^{+} + e^{-}} \nonumber\]

equals:

\[\ce{MnO4^{-} + V^{3+} + H2O -> HmnO4^{-} + VO^{2+} + H^{+}} \nonumber\]

under basic conditions:

\[\ce{MnO4^{-} + V^{3+} + H2O + OH^{-} -> HMnO4^{-} + VO^{2+} + H^{+} + OH^{-}} \nonumber\]

\[\ce{MnO4^{-} + V^{3+} + H2O _ OH^{-} -> HMNO4^{-} + VO^{2+} + H2O} \nonumber\]

\[\ce{MnO4^{-} + V^{3+} + OH^{-} -> HMnO4^{-} + VO^{2+}} \nonumber\]

Exercise 1.9.1:

The bonds to iron would contract because the increased charge on the iron would attract the ligand donor electrons more strongly. The bonds to copper would lengthen because of the lower charge on the copper.

Exercise 1.9.2:

1. Most likely there are repulsive forces between ligands if the bonds get too short.
2. Insufficient overlap between metal and ligand orbitals would weaken the bond and raise the energy.
3. The range of possible bond lengths gets broader as energy is increased. The bond has more latitude, with both longer and shorter bonds allowed at higher energy.

Exercise 1.9.6:

The reactants and products are very similar in this case. However, the Fe(III) complex has shorter bonds than the Fe(II) complex because of greater electrostatic interaction between the metal ion and the ligands. These changes in bond length needed in order to get ready to change from Fe(III) to Fe(II) (or the reverse) pose a major barrier to the reaction.

Exercise 1.9.7:

1. The drawing is an oversimplification, but in general the water molecules are shown reorienting after the electron transfer because of ion-dipole interactions. In this case, the waters are shown orienting to present their negative ends to the more positive iron atom after the electron transfer. In reality, in a protein there are lots of other charges (including charges on the ligand) that may take part in additional ion-dipole interactions.
2. Because electron transfer is so fast, atomic and molecular reorganisations are actually thought to happen before the electron transfer. The water molecules would happen to shift into a position that would provide the greatest possible stabilisation for the ions and then the electron would be transferred. A less polar solvent than water would be less able to stabilize ions and the electron would be slower to transfer as a result.

Exercise 1.10.1:

1. octahedral
2. In the first row, 2⁺ complexes are almost always high spin. However, 3⁺ complexes are sometimes low spin.

c)

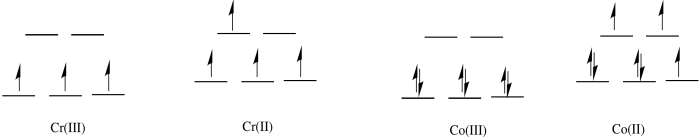
d) The Co(II) complex is high spin and labile. The ligands are easily replaced by water.

e) The Cr(III) complex is only d³; it is inert.

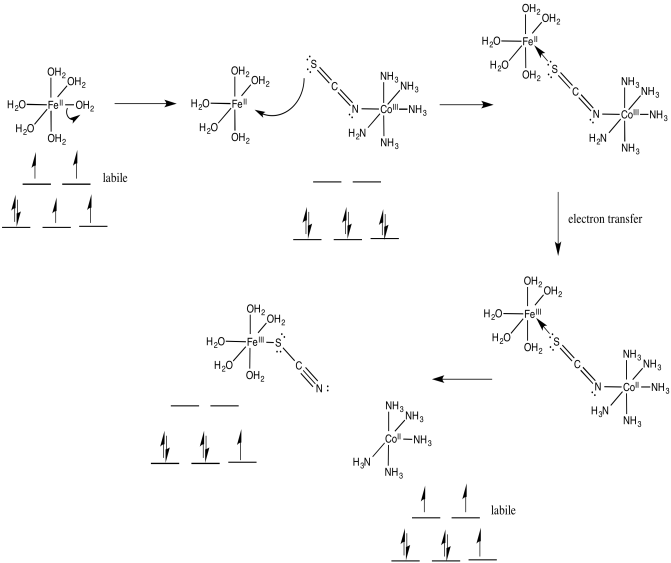
Exercise 1.10.3

Exercise 1.10.4:

a)

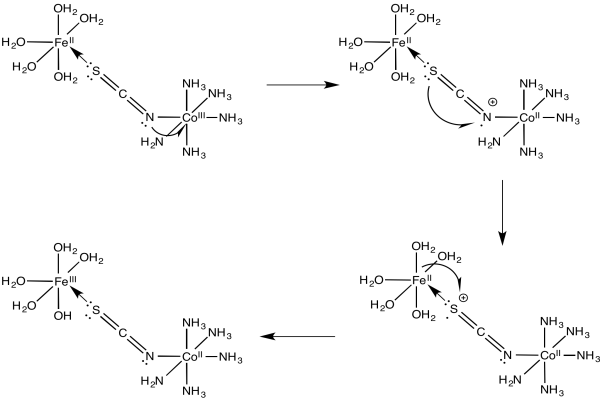
b)

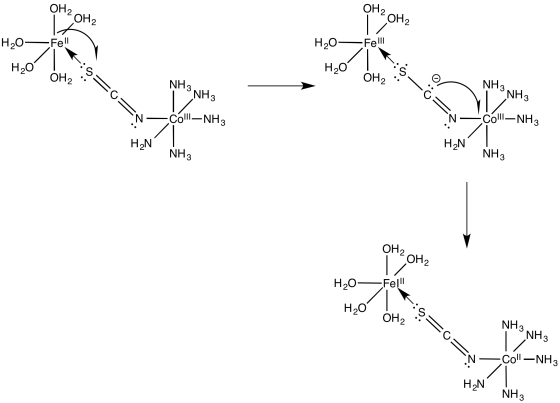
Exercise 1.11.1:

The compound undergoes a two-electron oxidation. The oxidized species then undergoes a two-electron reduction.

Exercise 1.12.2:

a) CH₂CHCH₃

C-H bonds	6-
C-X bonds	0
Oxidation Level	6-

CH₃CH₂CH₃

C-H bonds	8-
C-X bonds	0
Oxidation Level	8-

Propane results from a two-electron reduction of propene.

b) CH₃CH₂CHO

C-H bonds	6-
C-X bonds	2+
Oxidation Level	4-

CH₃CH₂CH₂OH

C-H bonds	7-
C-X bonds	1_
Oxidation Level	6-

Propanol results from a two-electron reduction of propanal.

c) CH₃CH(OH)CH₂CH₂OH

C-H bonds	8-
C-X bonds	2+
Oxidation Level	6-

CH₃COCH₂CHO

C-H bonds	6-
C-X bonds	4+
Oxidation Level	2-

3-oxobutanal results from a four-electron oxidation of 1,3-butanediol.

Exercise 1.12.3:

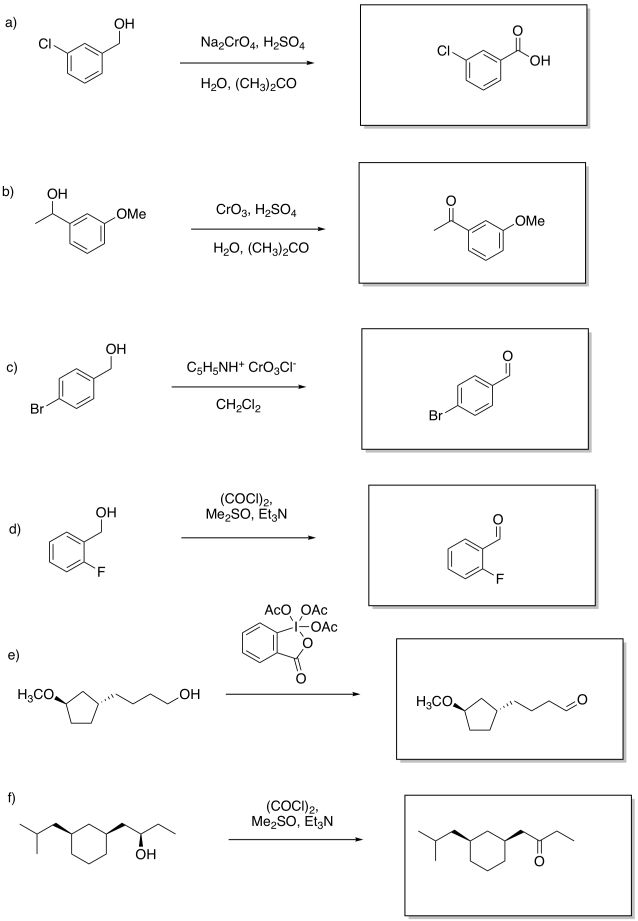
Exercise 1.12.4: