Skip to main content
Chemistry LibreTexts

5.7: Solutions to Selected Problems

  1. Last updated
  2. Save as PDF
  • Page ID
    200825

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Exercise 5.1.1:

    1. under an atmosphere of hydrogen gas.
    2. under an atmosphere of an inert gas such as nitrogen or argon, especially if there is a way for hydrogen gas to escape.

    Exercise 5.1.2:

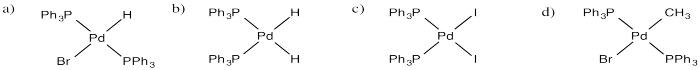
    OAvaskaAddn.png

    Exercise 5.2.1:

    1. Pd(0) to Pd(II) (I and Ph are negative)
    2. Rh(I) to Rh(III) (Cl and acyl are negative)
    3. Ni(II) to Ni(0) (Methyl and phenyl are negative)
    4. Zr(IV) to Zr(II) (Cp, H and Ph are negative)

    Exercise 5.2.2:

    Increased steric crowding in the coordination sphere may force two gorups to redcutively eliminate together.

    Exercise 5.3.1:

    1. Probably the first step is the hardest (slowest) step, involving bond breaking in the alkyl halide. The donation of the resulting anion to the cation should be pretty fast.
    2. \(Rate = k_{1}[ML_{n}][CH_{3}Br]\)

    Exercise 5.3.2:

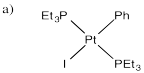
    OA3pt2soln.png

    b) Methanol is more polar than benzene. The acceleration of the reaction in methanol suggests that there is increasing polarity in the transition state, or polar intermediates.

    c) Inhibition by iodide ion suggests that iodide is a product of a reversible step during this reaction. Adding iodide pushes that step backward, decreasing the rate of product formation. The mechanism below is consistent with these observations:

    OA3pt2csoln.png

    Thus reductive elimination occurs as we go from the second to the third intermediate.

    Presumably, the increased positive charge (and general decrease in electron density, owing to loss of a ligand) results in reductive elimination because of destabilization of the Pt(IV).

    Alternatively, we might suppose that after loss of iodide, the iodide ion donates directly to a phenyl ligand, displacing the platinum as a leaving group in an SN2 reaction. That would lead directly to the product from the first intermediate, which is a simpler route. However, the precedent for aliphatic nucleophilic substitution involves nucleophilic donation to tetrahedral carbons, not to trigonal planar ones. That mechanism is unlikely.

    Exercise 5.3.3:

    1. Pt(0) to Pt(II)
    2. Changes from (R) to (S)
    3. This is an SN2 reaction, so the platinum displaces the bromide from the opposite side.

    Exercise 5.3.4:

    In case (a), the reaction appears to be SN2, presumably with complete inversion of configuration from (S) to (R). In case (b), there is probably a competing SN1 pathway because the resulting cation is both benzylic and secondary, so it is pretty stable. On the other hand, if the reaction proceeded entirely through an SN1 pathway, the reaction would result in nearly complete racemization, with 0% ee.

    Exercise 5.3.5:

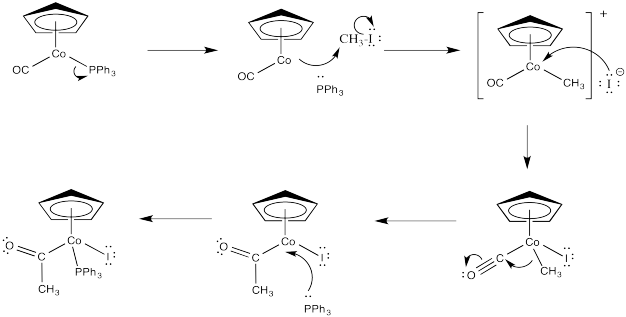
    OA3pt5soln.png

    Exercise 5.3.6:

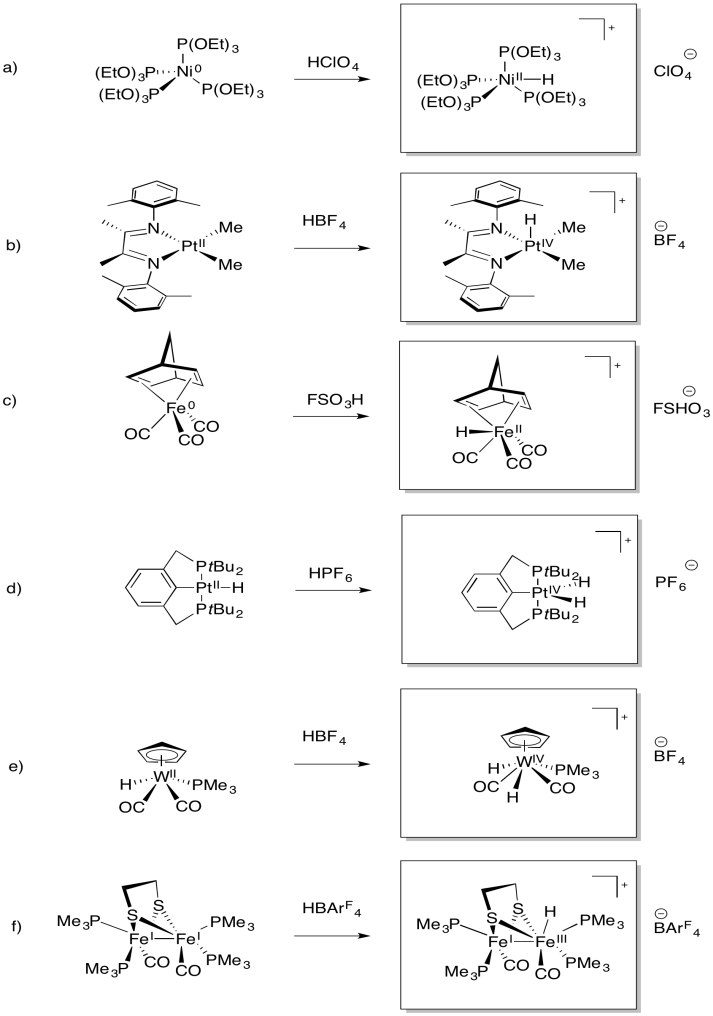
    OAprotonsoln.png

    Exercise 5.4.1:

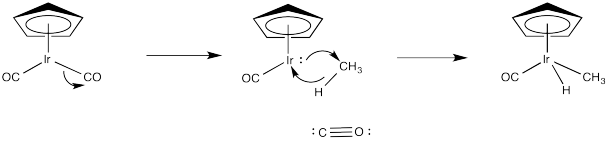
    OA4pt1soln.png

    Exercise 5.4.2:

    Concerted oxidative addition is the mechanism that occurs when a polar mechanism (SN2) is not possible. It is sometimes called "cis" oxidative addition. Because the two fragments added to the metal form bonds to the metal at the same time, they must be cis to each other.

    By the principle of microscopic reversibility, reductive elimination works the same way. The ligands have to be cis to each other in order to reductively eliminate, unless they are eliminating via a polar mechanism. Since both alkyl groups would have the same charge, a polar mechanism is unlikely.

    Both of these platinum(II) complexes are d8 and they would adopt square planar geometry. In the second case, the alkyls would be trans to each other and would be unable to undergo reductive elimination.

    Exercise 5.5.1:

    a) homogeneous b) heterogeneous c) heterogeneous d) homogeneous

    Exercise 5.5.2:

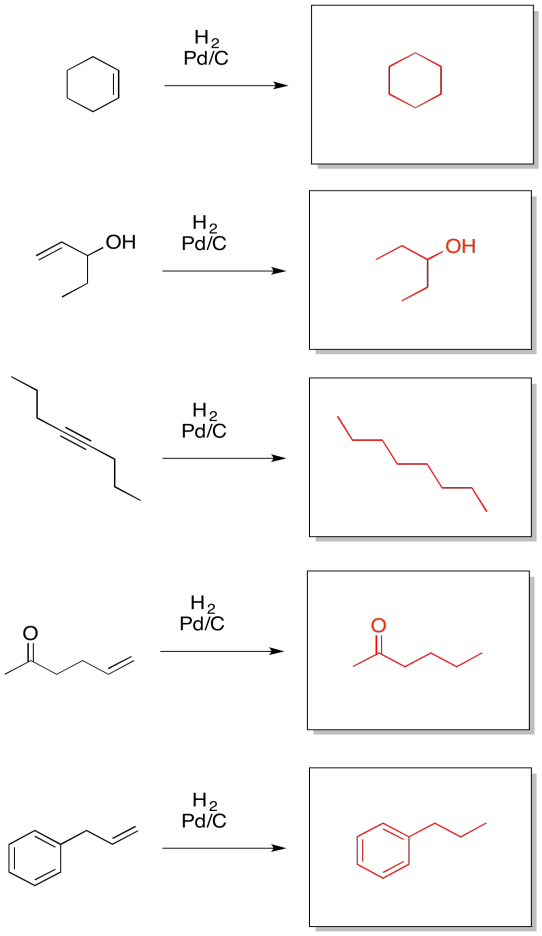
    OA5pt2soln.png

    Exercise 5.5.3:

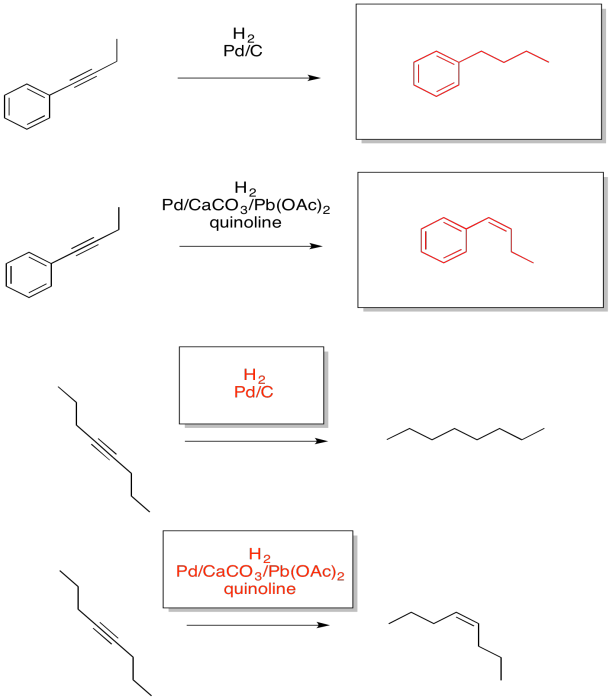
    OA5pt3soln.png

    Exercise 5.5.4:

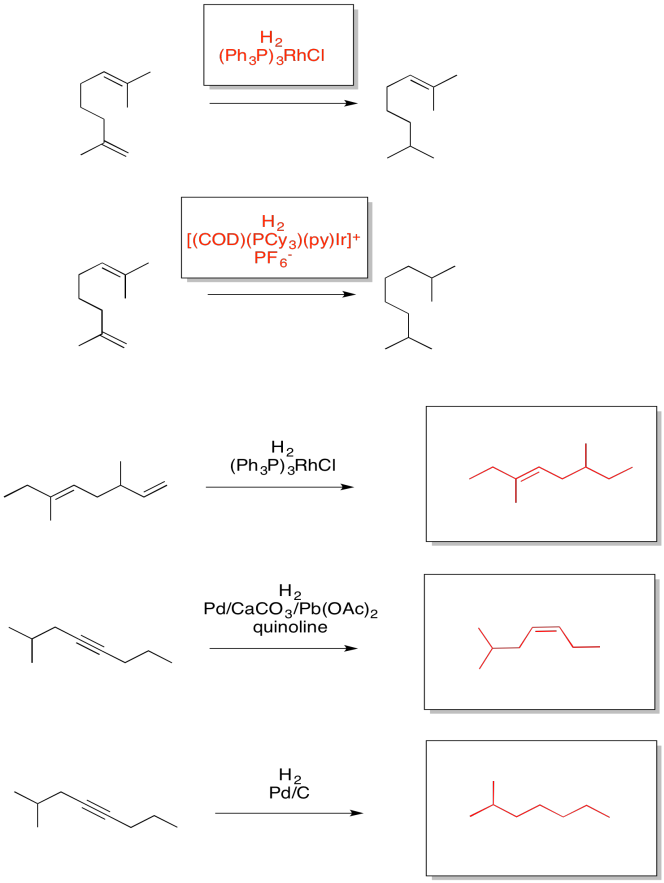
    OA5pt4soln.png

    Exercise 5.5.6:

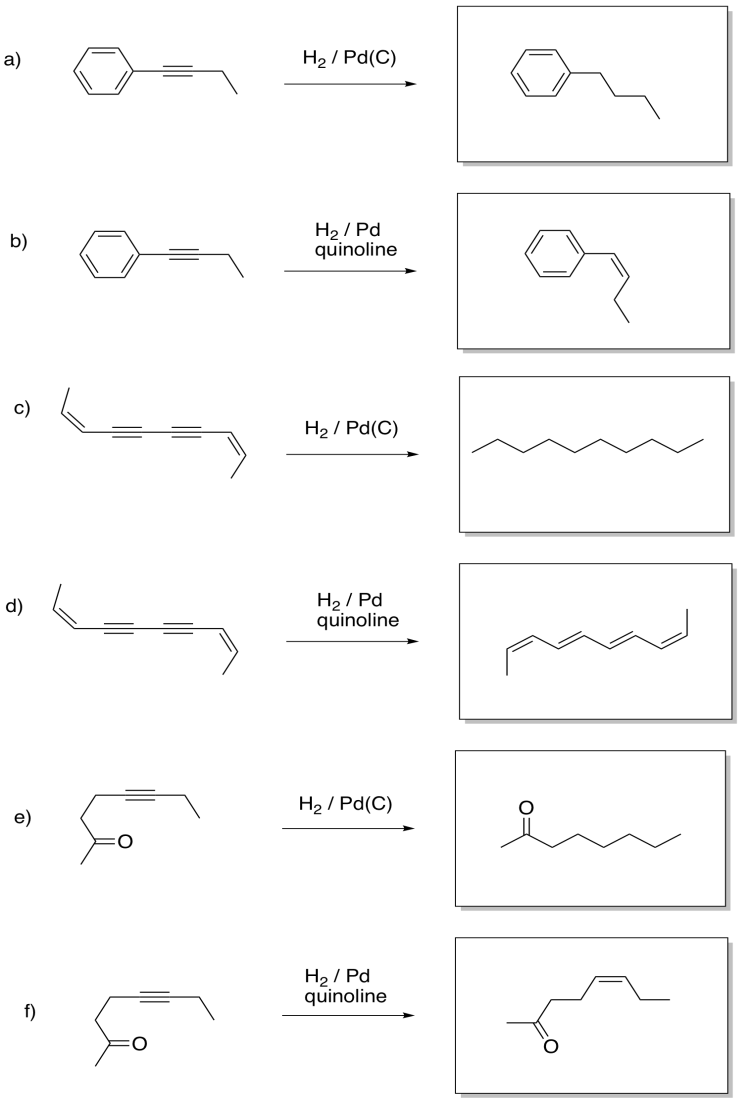
    OAH2Lindlarsoln.png

    Exercise 5.5.7:

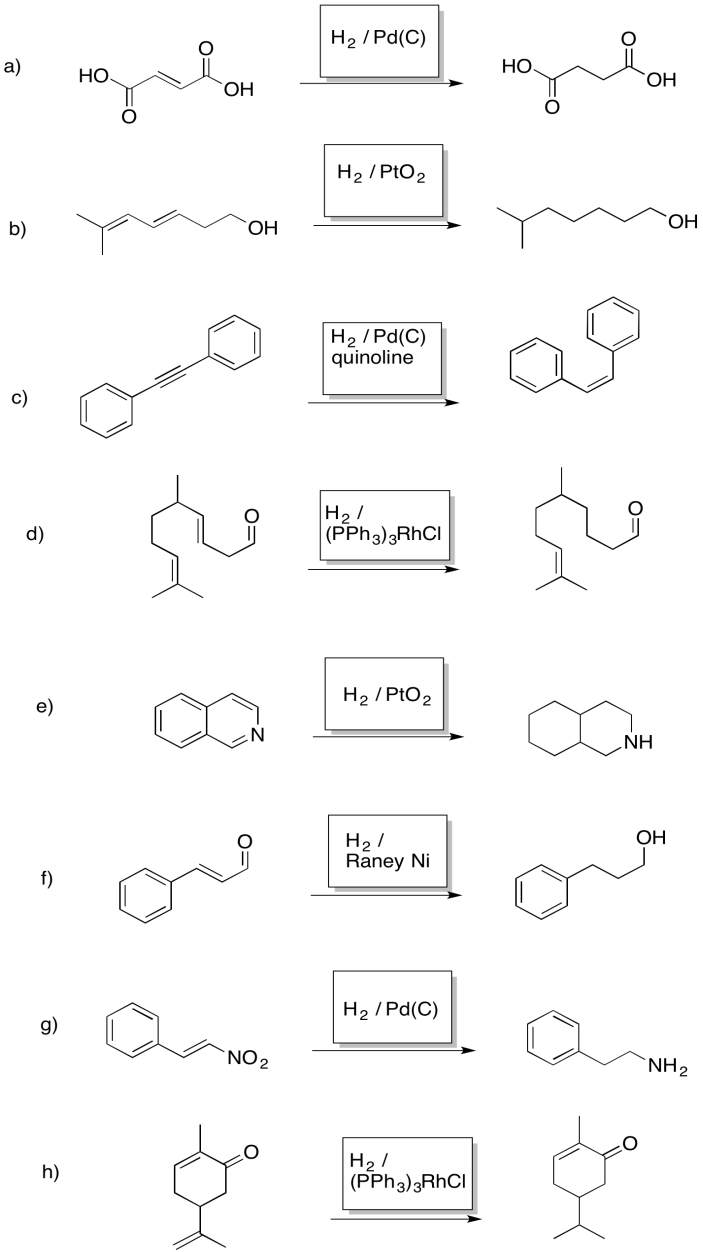
    OAH2mixedsoln.png

    Exercise 5.6.6:

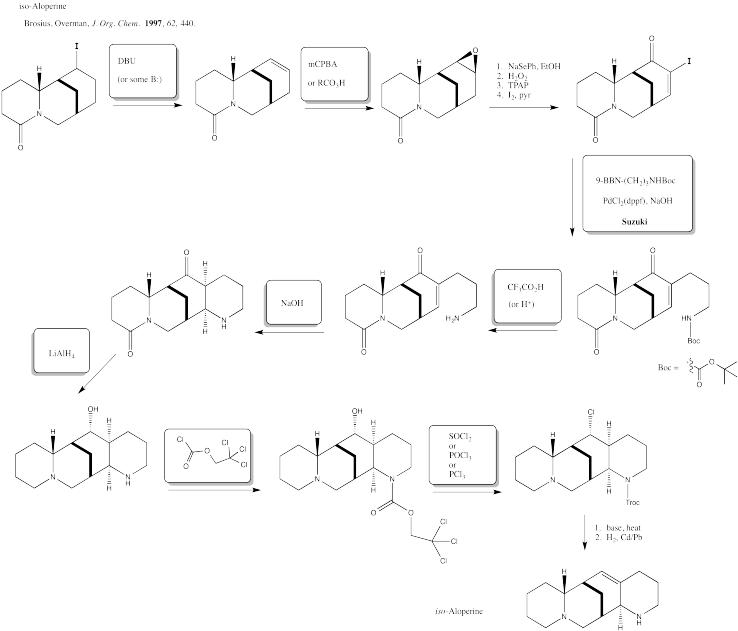
    AloperineAnswer.png

    Exercise 5.6.7:

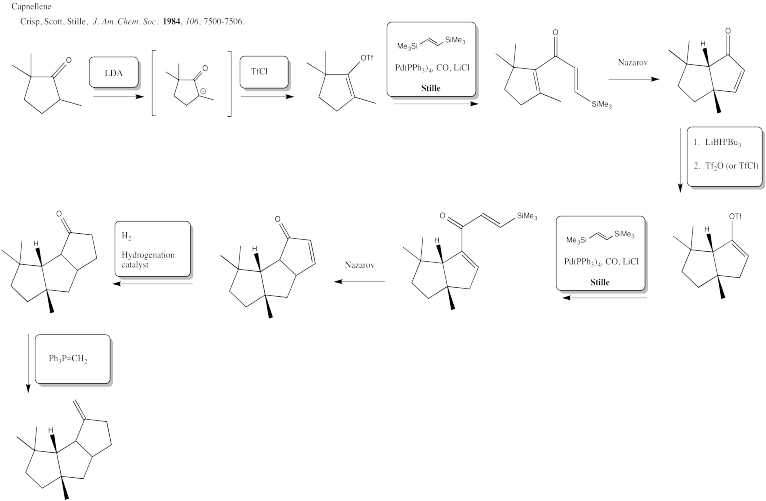
    CapnelleneAnswer.png

    Exercise 5.6.8:

    HistrionicotoxinAnswer.png

    This page titled 5.7: Solutions to Selected Problems is shared under a CC BY-NC 3.0 license and was authored, remixed, and/or curated by Chris Schaller via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.