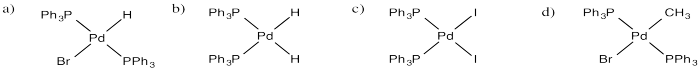5.1: Introduction
- Page ID
- 189860
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Oxidative addition and reductive elimination are key steps in industrial catalysis. Oxidative addition is used to activate substrates. Substrates that normally might not react get ready to react with something. Then they sit on the metal atom and wait for something else to come along and react with them.

Figure \(\PageIndex{1}\): A generalized oxidative addition.
Bonds can be broken via oxidative addition that cannot easily be broken via other reactions. For example, although the H-H bond is very strong, it can be cleaved in the presence of a variety of metal atoms and ions. Transition metals possess the right tools to coax the two hydrogen atoms apart from each other.

Figure \(\PageIndex{2}\): A generalized oxidative addition of dihydrogen.
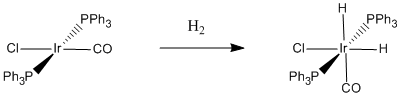
Figure \(\PageIndex{3}\): A specific case of oxidative addition of dihydrogen. When hydrogen adds to Vaska's complex, the oxidation state of iridium changes from +1 to +3.
Reductive elimination, in turn, is used to couple different groups together to form useful products. Once two groups are sitting beside each other on a transition metal atom or ion, they can bond to each other rather than the metal and go off together as a new molecule.

Figure \(\PageIndex{4}\): A general scheme for reductive elimination.
Clearly, a reductive elimination is just an oxidative addition in reverse. The reaction can go in either direction. That means it can, conceivably, occur in equilibrium. At this level, you would not be expected to know which direction would be favored for a particular reaction. However, you might be able to predict which direction a reaction would proceed based on factors such as le Chatelier's principle.
- le Chatelier's principle says that a change in the reaction conditions will lead to a shift in product:reactant ratio that offsets the change
For example, adding more reactant to the reaction shifts equilibrium to the right. More product is made, and some of the extra reactant is used up, so that the system can come back to its natural equilibrium. If products are somehow removed from the system, the reaction will also shift to the right, using up reactants and replacing the missing product. If the reaction is exothermic (produces heat) and more heat is added to the system, the reaction would shift to the left, using up some products and making more reactants in order to remove excess heat.
The reversibility of oxidative addition / reductive elimination actually serves very well in catalytic processes. For example, one of the most important catalytic processes in the world is catalytic hydrogenation, in which two hydrogen atoms are added across a double bond (usually a C=C bond, but sometimes a C=O or C=N bond). The process requires oxidative addition of hydrogen to a metal, but it also requires reductive elimination of an alkyl and a hydride to form the final product, forming a hydrocarbon.
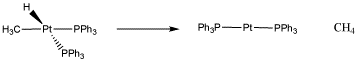
Figure \(\PageIndex{5}\): A reductive elimination of a methyl and a hydride to form methane.
The addition of dihydrogen to Vaska's complex and other transition metals is a reversible reaction. The hydrogen can be released again if the reaction moves to the left in a reductive elimination. That reversibility makes transition metal compounds useful for hydrogen storage. Hydrogen gas is voluminous, flammable and generally dangerous. By cleaving H2 and binding hydrogen to metal atoms, hydrogen can be more safely stored and released again under the right conditions.
In reductive elimination, bonds can be made that cannot be formed via other reactions. That makes it a useful part of strategies to make commodity chemicals and complex organic molecules such as pharmaceuticals.
Based on le Chatelier's principle, propose conditions under which:
a) Vaska's complex could bind hydrogen
b) the resulting dihydride adduct of Vaska's complex could release dihydrogen again.
- Answer a
-
under an atmosphere of hydrogen gas.
- Answer b
-
under an atmosphere of an inert gas such as nitrogen or argon, especially if there is a way for hydrogen gas to escape.
Draw products of oxidative addition of the following compounds to (PPh3)2Pd.
a) HBr b) H2 c) I2 d) CH3-Br
- Answer
-