3.7: The Trans Effect
- Page ID
- 200515
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
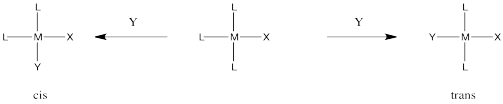
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Occasionally in ligand substitution there is a situation in which there are two identical ligands that could be replaced, but two different products would result depending on which ligand left. This situation often happens in square planar complexes, for example. Replacement of one ligand would lead to a cis product. Replacement of the other one would lead to a trans product.
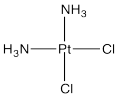
An important example of this issue is in the synthesis of cis-platin, an antitumour medication frequently used to treat ovarian and testicular cancer.
Cis-platin could be made from treatment of tetraammineplatinum(II) with chloride salts. The chloride ion could replace two of the ammonia ligands.
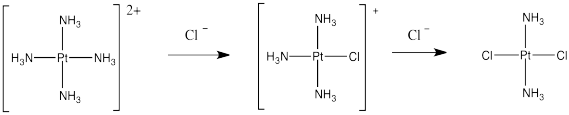
But that doesn't work. That synthesis results in the formation of trans-platin, a compound that has all of the nasty side effects of the cis isomer but with none of the therapeautic benefit.
If instead you were to start with tetrachloroplatinate salts and treat them with ammonia, you could replace two of the chloride ligands. That works really well, and it provides cis-platin, not trans-platin.

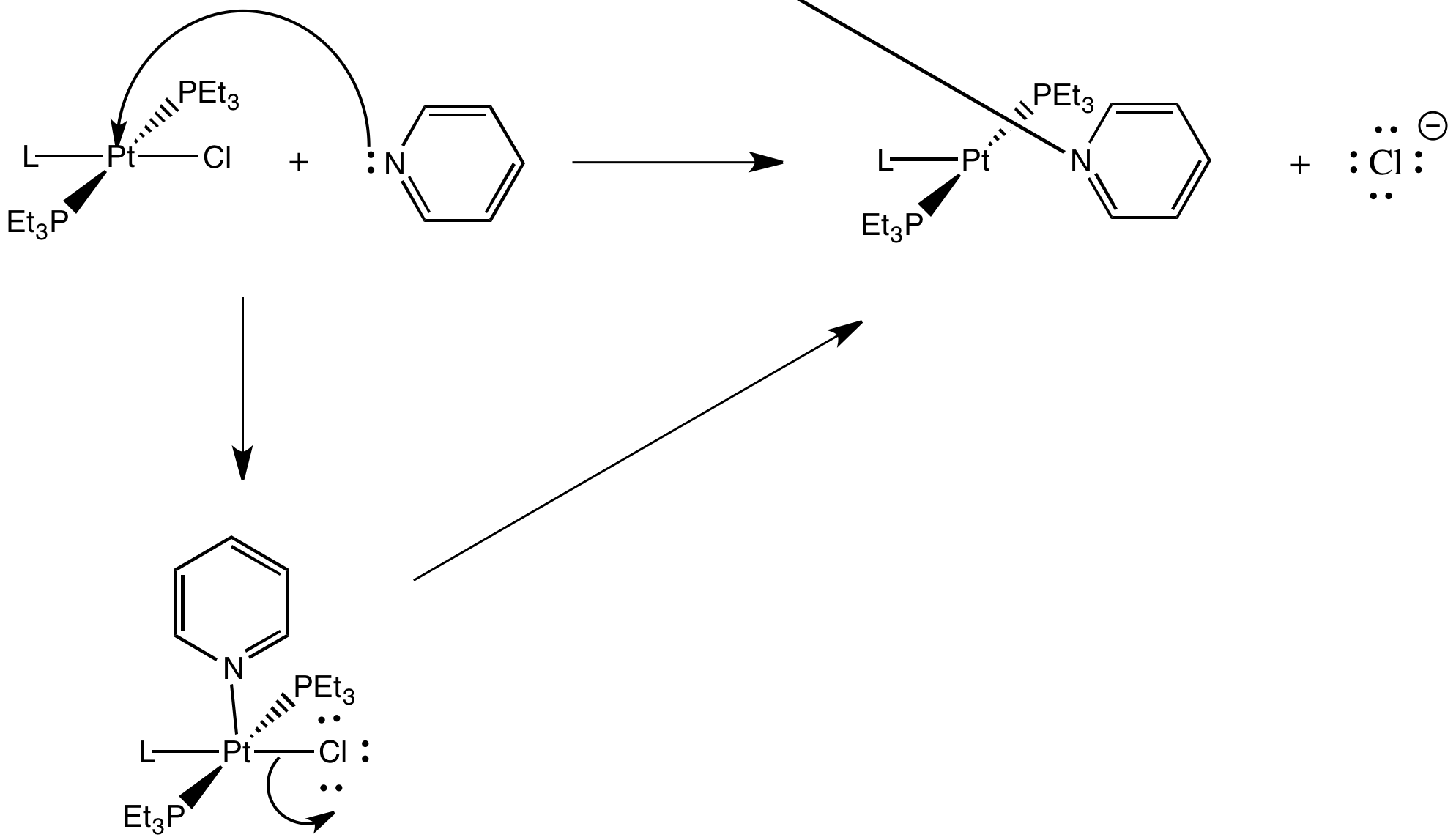
What do you think is the mechanism of substitution of the two reactions above? Why?
- Answer
-
This is probably an associative mechanism because of the square planar geometry.
This reaction, if run under these conditions, is clearly not always under thermodynamic control. Two different products result, depending on how the reaction is done. One of those isomers is probably more stable than the other; if thermodynamics were in charge, it would form the same thing both times.
Instead, there may be an element of kinetic control for at least one of the pathways. A given product might be made, not because it is more stable, but simply because it forms more quickly than the other one.
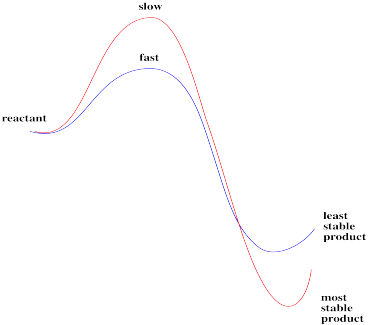
Take another look at those two reactions. One of the things that they have in common is that the ligand that gets replaced is trans to a chloride. It is not trans to an ammonia. Maybe the other ligands in the complex can influence how quickly one ligand can leave.

Specifically, the "trans effect" is the role of trans-ligands in influencing substitution rates in square planar complexes.
The following kinetic data were obtained for substitutions on square planar platinum complexes, in the reaction:
\[trans-(PEt_{3})_{2}PtLCl + py \rightarrow trans-(PEt_{3})_{2}PtLpy^{+} + Cl^{-} \nonumber\]
| L | kobs (s-1) | T, °C |
| PMe3 | 0.20 | 0 |
| H- | 0.047 | 0 |
| PEt3 | 0.041 | 0 |
| CH3- | 6.0 x 10-4 | 25 |
| C6H5- | 1.2 x 10-4 | 25 |
| Cl- | 3.5 x 10-6 | 25 |
Ref: Cooper Langford & Harry Gray, Ligand Substitution Processes, W.A. Benjamin, NY, 1965, p. 25.
Draw structures for each of the complexes listed in the table.
- Answer
-

Provide a mechanism with arrows for the reaction studied in the table.
- Answer
-
Clearly that trans ligand has a dramatic effect on how quickly the chloride can be substituted in the above study. Additional studies like this one have led to some general trends. Below, the ligands on the left have strong trans-effects. Ligands trans to them are substituted very quickly. The ligands on the right have very modest trans effects. Ligands trans to them are substituted only slowly.
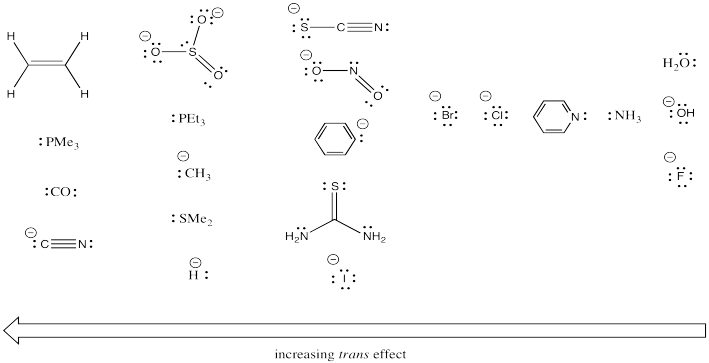
Look for empirical trends in the series of ligands above. Without trying to explain exactly why, find chemically relevant factors that may be responsible for these reactivity trends.
- Answer
-
There is an electronegativity trend: the less electronegative, the greater the trans effect (see the halogens, as well as the series O,N,C and also the orders within several pairings: S,P; O,S and N,P).
Alternatively, some of the above could be described by a polarizability trend: more polarizable atom, greater trans effect (for example, the halogens).
Most of the ligands containing π-bonds have strong trans influence (but not all).
Most of the π-donors have a weaker trans influence. However, these ligand cover a very broad range in this series.
In general, explanations of the trans effect have focused on two separate types of ligands. These are strong sigma donors and strong pi acceptors.
Strong sigma donors donate electrons very effectively to the metal via a sigma bond. Because the ligand trans to this donor would be bonding via donation to the same metal p orbital, there is a competition. The metal p orbital bonds more favorably with the strong sigma donor, and the ligand trans to it is left with a weaker bond.
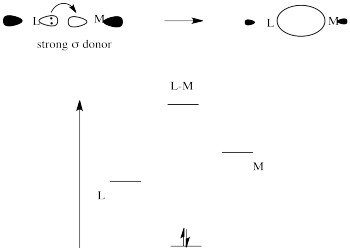
The strong sigma donor gets good overlap with the metal orbital and the resulting interaction goes down low in energy.
The weak sigma donor gets poorer overlap with the metal orbital and only weak stabilization of the donor electrons.
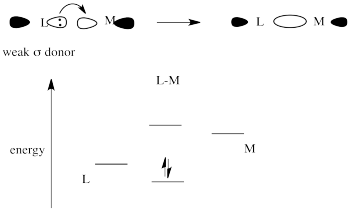
Place these two choices together, and the metal orbital will engage in a strong bonding interaction with the strong σ-donor. Doing so lowers the electronic energy significantly. It won't interact very much with the weak σ-donor, because doing that won't result in as much lowering of electronic energy. The result is a strong bond on one side of the metal and a weak bond on the other. That weak bond will break easily and that ligand will be replaced easily.
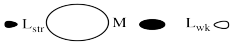
Which of the ligands in the trans effect series are probably strong σ-donors? Why?
- Answer
-
The strongest σ-donors are typically those with more polarizable donor atoms (such as S, P, I) as well as those with less electronegative donor ions such as C- and H-.
Strong pi acceptors exert their trans effect in a different way. They are thought to stabilize a particular geometry of the five-coordinate intermediate in substitution of square planar complexes. We haven't worried too much about the geometry of that intermediate, but it is probably trigonal bipyramidal. It would have three ligands in an equatorial plane and two more directly opposite each other, in the axial positions.
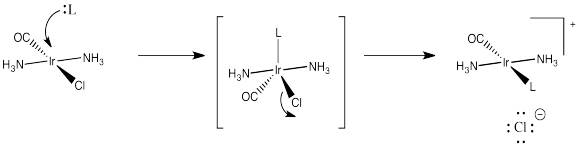
Essentially, the incoming ligand pushes two of the ligands down from the square plane to form this trigonal bipyramid. When it comes time for a ligand to leave, it is probably going to be one of these ligands that is already on the move. They are already on a trajectory out of the square plane, anyway.
A strong pi acceptor like CO exerts its trans effect by making sure it, along with the ligand opposite it, gets into that equatorial plane. It does that by a stabilizing delocalization that happens when the π-acceptor is in the electron-rich equatorial plane. In that position, it can draw electron density via π-donation from two different donors. If it were in an axial position, it could still delocalize electrons this way, but it would draw most effectively from just one donor rather than two.
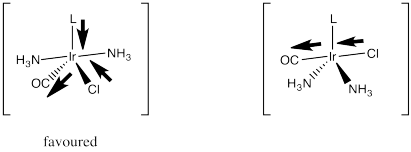
So which of those two ligands is going to keep moving and leave the complex? It certainly won't be the one that is exerting a stabilizing, delocalizing effect on the complex via its strong bonding interactions. It will be the unlucky trans ligand that got dragged along with it.
Which of the ligands in the trans-effect series are probably strong π-acceptors? Show why.
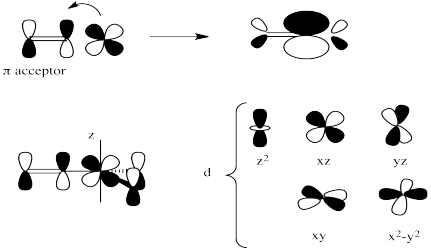
Draw an orbital picture showing the -delocalization described in the trigonal bipyramidal intermediate. Label the orbitals, assuming the z axis is along the axis of the trigonal bipyramid (i.e. the equatorial plane is the xy plane).
- Answer
-
Substitution of trans ligands in μ-oxo-bis(μ-acetato)diruthenium complexes: Synthesis and kinetic studies. Hussain, Bhatt, Kumar, Thorat, Padhiyar and Shukla, Inorganica Chemica Acta, 2009, 362, 1101-1108.
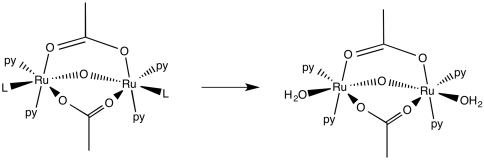
Given the structure [Ru2O(L)6(acetate)2](PF6)2, in which L is a neutral donor,
a) Draw the structure of the counterion, PF6-.
b) Provide an account of the valence electron count in the ruthenium coordination complex.
| Valence electrons on metal | |
| Total charge on ligands | |
| Charge on the metal | |
| Revised count on metal | |
| Electrons donated by ligands | |
| Total electrons on metal in complex |
Data shows that the ligands L are trans to the bridging oxo ligand are labile.
c) Use orbital cartoons and words to provide an explanation for this effect.
When water is added to an acetone solution of [Ru2O(pyridine)4(L)2(acetate)2](PF6)2, then [Ru2O(pyridine)4(H2O)2(acetate)2](PF6)2 is formed.
d) Draw the product of this reaction.
When pyridine is added to [Ru2O(pyridine)4(H2O)2(acetate)2](PF6)2, then [Ru2O(pyridine)6(acetate)2](PF6)2 is formed. The following rate constants were observed for this reaction.
| [pyridine] mol L-1 | kobs s-1 (x 10-3) |
| 0.005 | 1.75 |
| 0.012 | 2.53 |
| 0.025 | 9.7 |
| 0.049 | 16.7 |
| 0.100 | 35.2 |
e) Use the data from this table to determine the order in pyridine. Provide an explanation for your conclusion.
f) Draw a mechanism for the reaction, consistent with the data.
g) Write a rate law for the reaction.
h) The authors studies the same reaction with different ligands instead of pyridine. They observed an increase in rate constants with increasing basicity of the incoming ligands. Provide an explanation for this observation.
- Answer a
-

- Answer b
-

- Answer c
-
The oxo is a strong sigma donor and hogs the orbital with the metal thus leaving very little room for orbital bonding trans to the sigma donor.
- Answer d
-
- Answer e
-
First order. Although there is some amount of error in the data, doubling the pyridine concentration generally results in a doubling of the rate.
- Answer f
-
The mechanism you draw would have to involve a first associative step; because the complex is already 18 electrons, associative interchange is likely.
- Answer g
-
\[Rate = k [ML_{n}][py] \nonumber\]
- Answer h
-
Basic ligands have stronger attraction to the metal thus accelerating the reaction.


