3.5: Activation Parameters
- Page ID
- 189850
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The rate law shows how the rate of a reaction depends on concentrations of different species in solution. The proportionality constant, k, is called the rate constant. It contains other information about the energetic requirements of the reaction.
All reactions must overcome activation barriers in order to occur. The activation barrier is the sum of the energy that must be expended to get the reaction going. An activation barrier is often thought of, cartoonishly, as a hill the molecule has to climb over during the reaction. Once, there, it can just slide down the other side of the hill to become products. At the top of the hill, the molecule exists in what is called the "transition state". At the transition state, the structure is somewhere between its original form and the structure of the products.
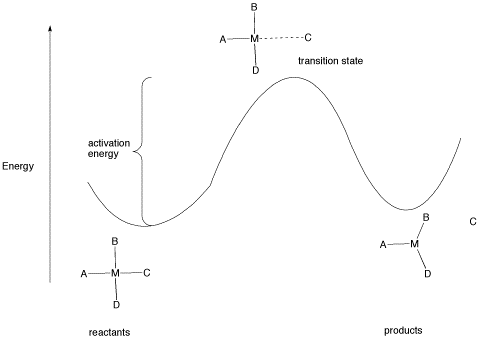
The type of diagram shown in figure LS6.1 is sometimes called a "reaction progress diagram". It shows energy changes in the system as a reaction proceeds. One or more activation barriers may occur along the reaction pathways, as various elementary steps occur in the reaction. In the above case, it is easy to imagine the source of the energy barrier, because some energy must be expended to break the bond to ligand C.
However, after that barrier is passed, energy is lowered again. This can happen for several reasons. Once C has separated from the metal complex, it is free to vibrate, tumble, roll and zip around all on its own. That means it can put its energy into any of those modes, independently of the metal complex. As a result, the entropy of the system increases. That lowers the overall "free energy" of the system. In addition, there may be some relief of crowding as the molecule changes from a four-coordinate complex to a three-coordinate complex, so strain energy is also lowered.
Make drawings depicting the relationship between reaction progress and energy for the following cases:
a) a new ligand binds to a four-coordinate complex, forming a five coordinate complex.
b) a two-step process in which a new ligand binds to a four-coordinate complex, forming a five coordinate complex, and then an old ligand dissociates to form a new, four-coordinate complex.
The rate constant gives direct insight into what is happening at the transition state, because it gives us the energy difference between the reactants and the transition state. Based on that information, we get some ideas of what is happening on the way to the transition state.
The rate constant can be broken down into pieces. Mathematically, it is often expressed as
\[k = (\frac{RT}{Nh}) e^{-\frac{\Delta G \ddagger}{RT}} \nonumber\]
In which R = the ideal gas constant, T = temperature, N = Avogadro's number, h = Planck's constant and Δ G‡ = the free energy of activation.
The ideal gas constant, Planck's constant and Avogadro's number are all typical constants used in modeling the behaviour of molecules or large groups of molecules. The free energy of activation is essentially the energy requirement to get a molecule (or a mole of them) to undergo the reaction.
Note that k depends on just two variables:
- Δ G‡ or the energy required for the reaction
- T or the temperature of the surroundings, which is an index of the available energy
The ratio of activation free energy to temperature compares the energy needs to the energy available. The more energy available compared to the energy needed, the lower this ratio becomes. As a result, the exponential part of the function becomes larger (since the power has a minus sign). That makes the rate constant bigger, and the reaction becomes faster.
The activation free energy is constant for a given reaction. It can be broken down in turn to:
\[\Delta G^{\ddagger} = \Delta H^{\ddagger} -T \Delta S^{\ddagger} \nonumber\]
in which Δ H‡ = activation enthalpy and Δ S‡ = activation entropy.
The activation enthalpy is the energy required for the reaction. The activation entropy deals with how the energy within the molecule must be redistributed for the reaction to occur. These two parameters can be useful in understanding events leading to the transition state.
For example, in ligand substitution, an associative pathway is marked by low enthalpy of activation but a negative entropy of activation. The low enthalpy of activation results because bonds don't need to be broken before the transition state, so it doesn't cost much to get there. That's favorable and makes the reaction easier. However, a decrease in entropy means that energy must be partitioned into fewer states. That's not favorable and makes the reaction harder. The reason the energy must be redistributed this way is that two molecules (the metal complex and the new ligand) are coming together to make one bigger molecule. They can no longer move independently of each other, and all of their combined energy must be reapportioned together, with a more limited range of vibrational, rotational and translational states to use for that purpose.
- Associative pathway: more bond making than bond breaking; lower enthalpy needs
- Associative pathway: two molecules must be aligned and come together; fewer degrees of freedom for energy distribution; decrease in entropy
On the other hand, the dissociative pathway is marked by a higher enthalpy of activation but a positive entropy of activation. The higher enthalpy of activation results because a bond must be broken in the rate determining step. That's not favorable. However, the molecule breaks into two molecules in the rate determining step. these two molecules have more degrees of freedom in which to partition their energy than they did as one molecule. That's favorable.
- Dissociative pathway: more bond breaking in rate determining step, higher enthalpy needs
- Dissociative pathway: one molecule converts to two molecules in rate determining step, greater degrees of freedom in two independently moving molecules, entropy increases
Thus, looking at the activation parameters can reveal a lot about what is going on in the transition state.
What factor(s) other than entropy might raise the free energy of the transition state going into an associative step between a metal complex and an incoming ligand? (What factor might make the first, associative step slower than the second, dissociative step?)
- Answer
-
The metal centre is becoming more crowded as the new ligand arrives, so an increase in energy owing to steric hindrance may also play a role in the transition state energetics.
Other mechanisms for ligand substitution are also possible. The following case is referred to as an associative interchange (IA).
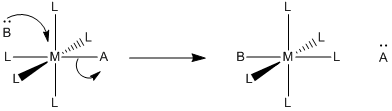
a) Describe in words what happens in an associative interchange.
b) Predict the rate law for the reaction.
c) Qualitatively predict the activation entropy and enthalpy, compared with
i) an associative mechanism and
ii) a dissociative mechanism.
- Answer a
-
The new ligand, B, is arriving at the same time as the old ligand, A, is departing. We might also describe it as new ligand B pushing old ligand A out of the complex.
- Answer b
-
\(Rate = k[ML_{5}A][B]\), which looks like an associative rate law.
- Answer c
-
This is a thought-provoking question without a definite answer. Associative mechanisms typically have lower activation enthalpy than dissociative mechanisms, because there has also been some bond-making prior to the bond-breaking in the rate determining step. The associative interchange would be a little more like the associative mechanism than dissociative. The mix of bond-making and bond-breaking at the transition state would make the enthalpy of activation relatively low.
Associative mechanisms have negative activation entropies, whereas dissociative mechanisms have positive activation entropies. The associative interchange could be in between the two, given that the elementary step would be close to entropically neutral overall. What happens at the transition state is a little harder to imagine, but it might reflect the small changes in entropy through the course of the reaction, producing a small entropy of activation. On the other hand, if the incoming ligand is forced to adopt some specific approach as it comes into the molecule (to stay out of the way of the departing ligand, for example) then that restriction could show up as a small negative activation entropy.
For the following mechanism:
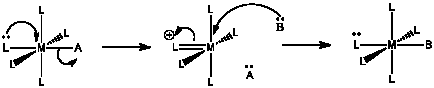
a) Describe in words what is happening.
b) Predict the rate determining step.
c) Predict the rate law for the reaction.
d) Qualitatively predict the activation entropy and enthalpy, compared with
i) both an associative mechanism and
ii) a dissociative mechanism.
e) Suggest some ligands that may be able to make this mechanism occur.
- Answer a
-
The lone pair donation from one ligand appears to push another ligand out.
- Answer b
-
The first step is probably rate determining, because of the bond breaking involved.
- Answer c
-
If the first step is rate determining, \(Rate = k [ML_{5}A]\).
- Answer d
-
Another question without a very clear answer. Compared with an associative mechanism, the activation entropy is probably much more positive, because additional degrees of freedom are being gained as the molecule heads over the activation barrier and one of the ligands separates to be on its own. However, the activation entropy may be less positive than in a regular dissociation, because in this case the breaking of one bond has to be coordinated with the formation of another.
The enthalpy of activation has both a bond-making and bond-breaking component, a little like in an associative mechanism. However, the amount of bond making here is probably less important, because pi bonds are typically not as strong as sigma bonds. The activation enthalpy is probably higher than an associative pathway but not as high as a dissociative one.
- Answer e
-
The donor ligand must have a lone pair. Oxygen donors would be good candidates, because even if one lone pair is already donating in a sigma bond, an additional lone pair may be available for pi donation. The same thing is true for halogen donors. It would also be true for anionic nitrogen donors but not for neutral nitrogen donors, because a neutral nitrogen has only one lone pair.


