1.9: Solutions to Selected Problems
- Page ID
- 200369
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise 1.2.7:
a) Scarlet molecules are disappearing over time. Ultramarine molecules are appearing over time. However, the number of scarlet molecules seems to stabilize around half its original number; the number of ultramarine molecules reaches about the same level. It is possible that the scarlet molecules are converted into the ultramarine ones, but reach an equilibrium. At this equilibrium, there happen to be about equal amounts of the two compounds.
b) Because the rate of growth of the tan molecules seems to track the rate of loss of the brown ones, it seems likely that the brown ones are being converted to tan molecules. At some point, the change levels out, so an equilibrium is reached. At this equilibrium, tan molecules outnumber brown ones.
c) Viridian molecules seem to be converting into gold ones but the system reaches equilibrium, at which point there are still more viridian molecules than gold ones.
Exercise 1.3.3:
a) e 2 < e 10
b) e 1/4 < e 1/2
c) e -3 > e -4
d) e -1/2 < e -1/3
Exercise 1.3.4:
a) Orientation (i) looks most likely to result in connection of the oxygen to carbon with displacement of bromide. In orientation (iii), the oxygen appears ready to collide with the bromine atom. and in oreientation (ii), it may collide with a hydrogen atom.
In addition, you will see later that bringing the the oxygen in along the C-Br axis (but away from the bromine) is also more likely to break the C-Br bond, for reasons involving molecular orbital overlap.
b) Orientation (ii) looks like the carbon anion in the acetylide ion is most likely to bond with the carbonyl carbon. In option (i), the carbon is going to collide with the carbonyl oxygen. In option (iii), it may collide with the alpha carbon, next to the carbonyl. Having the nucleophile approach from outside the plane of the carbonyl, as in option (ii), lowers the chance of collision with atoms other than the carbonyl carbon.
Again, there are also molecular orbital reasons that make this approach the preferred one.
Exercise 1.3.5:
a) We would expect the lowest barrier for breaking the Cr-CO bond. The barrier to break the Mo-CO bond would be just slightly lower than to break the W-CO bond.
b) Based on this information alone, we might expect the Cr-CO cleavage to occur most rapidly. Mo-CO cleavage would be slightly faster than W-CO cleavage.
Exercise 1.3.6:
- On this basis alone, we would expect the lowest barrier for C=C cleavage, followed by C=N and then C=O with the highest barrier.
- This trend is exactly the opposite of what we just predicted based on bond strengths.
- There may be a few different reasons for these differences. For example, the electrophilicity of the carbon may be a factor. Based on electronegativity differences, the C=O carbon should be most positive, the C=N carbon less so and the C=C carbon not at all. That electrophilicity may raise the reactant a little in energy.
Alternatively, there may be charge stabilization factors in the first-formed intermediate, which may be reflected in the transition state on the way there. These three differing atoms (O, N, C) are all found in a row of the periodic table, so electronegativity differences should dominate charge stability. The alkoxide ion would be most stable, the amide ion of medium stability and the alkyl anion least stable of all. That trend would lower the barrier to alkoxide formation and raise the barrier to formation of a carbon-based alkyl anion.
Exercise 1.4.1:
The vacancies in the crystal lattics give other atoms places to move into, sothey act as a path through which atoms can move. Diffusion through the solid is greatly accelerated.
Exercise 1.4.2:
a) The small, red dots are in the gas phase, so they are distributed throughout the container. The larger, gray dots are the solid, which lies along the bottom of the container.
b) The solid on the left is divided into finer particles, with much more surface area. If the gas reacts on the surface of the solid, reaction will be much faster on the left.
Exercise 1.4.3:
All three of these solvents have dipole moments. Also, all three molecules have oxygen lone pairs, so they are able to accept hydrogen bonds from hydrogen bond donors.
However, some of the solvents are much more polar than others. Water is capable of donating hydrogen bonds, because of its partially positive hydrogen attached to oxygen. It is the most polar of these solvents.
DMF is also very polar, because it has a polar C=O bond. This particular carbonyl is more like +N=C-O- because of lone pair donation from the nitrogen, so it is quite polar and will interact strongly with other species via dipole-dipole forces (or ion-dipole forces, if the other molecule is a salt).
THF only has a moderate dipole compared to the others. Although it will still interact via dipole-dipole (or ion-dipole) forces, it does so less effectively than water or DMF.
Exercise 1.4.4:
Water would be a very good solvent for (a) and (d), because both of those molecules would be very good at hydrogen bonding. Although water may be able to dissolve small amounts of the others, their solubility would be limited by the need for water molecules to release hydrogen bonds to each other in order to make room for the non-polar portions of these molecules.
THF would be able to dissolve the other molecules pretty well: (b), (c), (e) and (f). All of those molecules contain polar bonds, like THF, and could interact via dipole-dipole forces. THF would be able to dissolve small amounts of (a) and (d) but may not be polar enough to overcome the stronger intermolecular forces between these molecules.
DMF may be able to dissolve all of these molecules to a moderate extent. Although it is not a protic solvent, its dipole is enough to help overcome hydrogen bonding among (a) and (d).
Exercise 1.5.1:
Upper East Side. Lots more people per square foot.
Exercise 1.5.2:
a) 8.41 people km-2
b) 1,600 people km-2
c) 15.2 people km-2
d) 13.5 people km-2
e) 12.7 people km-2
f) 1,930 people km-2
g) 24.6 people km-2
Rank: Bahrain > Vatican > Jamaica > Argentina > China > Malawi > Russia
Exercise 1.5.3:
a) The volume is constant, but the number of molecules is increasing. The concentration is increasing.
b) The number of molecules is constant, but the volume is decreasing. The concentration is increasing.
Exercise 1.5.4:
In both cases, the molecules are becoming more densely packed. Collisions would become more frequent as we go from left to right.
Exercise 1.5.5:
a) The number of blue molecules is increasing, but the number of red molecules is staying the same.
b) Collisions between red and blue molecules would become more frequent as we go from left to right. The higher density of blue molecules makes collisions more likely.
c) The answer would stay the same.
d) The answer would stay the same qualitatively, but would differ quantitatively. The number of collisions would increase more sharply if the concentrations of both red and blue molecules increased, rather than just one concentration increasing.
Exercise 1.5.6:
a) A half dozen, a dozen, two dozen.
b) The concentration is doubling as we go left to right from one beaker to the next.
Exercise 1.5.7:
a) The elephant weighs \(6800kg \times 1000 \frac{g}{kg} = 6800000g = 6.8 \times 10^{6} g \)
b) We have \(47600 kg \times \frac{1 elephant}{6800 kg} = 7 elephants\). Very lucky.
c) \(7 mice \times 25 \frac{g}{mouse} = 175g\)
d) \(10 mice \times 25 \frac{g}{mouse} = 250g\)
Exercise 1.5.8:
The weight of 7 blue molecules = the weight of 2 red molecules. 1 red molecule = 7/2 x the weight of a blue molecule. \(MW_{red} = 3.5 \times MW_{blue} = 3.5 \times 60 \frac{g}{mol} = 210 \frac{g}{mol}\)
The weight of 6 blue molecules = the weight of 6 orange molecules. \(MW_{orange} = MW_{blue} 60 \frac{g}{mol}\)
The weight of 6 blue molecules = the weight of 1 grey molecule. \(MW_{grey} = 6 \times MW_{blue} = 6 \times 60 \frac{g}{mol} = 360 \frac{g}{mol}\)
Exercise 1.5.9:
A mole of material corrsponds to the numerical equivalent of the sum of atomic masses in an molecule, in grams.
a) atomic masses in NO2: 14 amu (N) + 32 amu (2 x O) = 46 amu. 1 mol of NO2 is 46 g of NO2.
b) 180 g
c) 106 g
d) 142 g.
Exercise 1.5.10:
a) \(3g \times \frac{1mol}{180g} = 0.017 mol\)
b) \(10g \times \frac{1mol}{106 g} = 0.094mol \)
c) \(30g \times \frac{142mol}{g} =0.21 mol\)
Exercise 1.5.11:
a) \(5g \times \frac{1mol}{180g} = 0.028mol; \frac{0.028 mol}{50mL} = 5.6 \times 10^{-4} \frac{mol}{mL} \times 1000 \frac{mL}{L} = 0.56 \frac{mol}{L}\)
b) \(11g \times \frac{1mol}{106g} = 0.104mol; \frac{0.104 mol}{25mL} = 4.16 \times 10^{-3} \frac{mol}{mL} \times 1000 \frac {mL}{L} = 4.2 \frac{mol}{L}\)
c) \(9g \times \frac{1mol}{156g} = 0.058 mol; \frac{0.058mol}{60mL} = 9.61 \times 10^{-4} \frac{mol}{mL} \times 1000 \frac{mL}{L} 0.96 \frac{mol}{L}\)
Exercise 1.6.1:
a) Rate of (a) = 1/2 x Rate of original
b) Rate of (b) = 1/2 x Rate of original
c) Rate of (c) = 3/4 x Rate of original
d) Rate of (d) = 1/2 x Rate of original; although the number of molecules is the same as the original, the volume is doubled. As a result, the concentration is cut in half.
e) Rate of (e) = 2 x Rate of original; although the number of molecules is the same as the original, the volume is halved. As a result, the concentration is doubled.
f) Rate of (f) = Rate of original; although the number of molecules is doubled, the volume is also doubled, leaving the concentration unchanged.
Exercise 1.6.2:
a) Rate of (a) = 1/2 x Rate of original
b) Rate of (b) = 1/2 x 1/2 = 1/4 x Rate of original
c) Rate of (c) = 2 x Rate of original
d) Rate of (d) = 1/2 x 1/2 = 1/4 x Rate of original; although the number of molecules is the same as the original, the volume is doubled. As a result, the concentration is cut in half.
e) Rate of (e) = 2 x 2 = 4 x Rate of original; although the number of molecules is the same as the original, the volume is halved. As a result, the concentration of each reactant is doubled.
f) Rate of (f) = Rate of original; although the number of molecules is doubled, the volume is also doubled, leaving the concentration unchanged.
Exercise 1.6.3:
a) Rate of (a) = Rate of original; the surface area of the white solid appears to be the same.
b) Rate of (b) = 1/2 x Rate of original; the surface area of the white solid appears to be cut in half.
c) Rate of (c) = 2 x Rate of original; the surface area of the white solid appears to be doubled.
d) The smaller sizes of the particles in (d) makes it harder to answer this question. Let's assume these white solids are spherical and that the radius of a sphere in (d) is half that of a sphere in the original. The surface area of a sphere is \(A = 4 \pi r^{2}\). The ratio of surface areas of one sphere to another is \(\frac{A_{1}}{A_{2}} = \frac{4 \pi r_{1}^{2}}{4 \pi r_{2}^{2}} = (\frac{r_{1}}{r_{2}})^{2}\). The ratio of surface areas of an original sphere to a sphere in (d) is \(\frac{A_{d}}{A_{0}} = (\frac{1}{2})^{2} = \frac{1}{4}\) However, there are 12 spheres in (d) and only 4 spheres in the original. Thus, the ratio of total surface areas \(\frac{A_{dT}}{A_{0T}} = (\frac{12}{4}) \times (\frac{1}{4}) = \frac{3}{4}\). The estimated rate of (d) = 3/4 x the Rate of original.
e) Let's assume these white solids are spherical and that the radius of a sphere in (e) is one quarter that of a sphere in the original. The ratio of surface areas of an original sphere to a sphere in (e) is \(\frac{A_{e}}{A_{0}} = (\frac{1}{4})^{2} = \frac{1}{16}\). However, there are 40 spheres in (e) and only 4 spheres in the original. Thus, the ratio of total surface areas \(\frac{A_{eT}}{A_{0T}} = (\frac{40}{4}) \times (\frac{1}{16}) = \frac{5}{8}\) The estimated rate of (e) = 5/8 x the Rate of original.
f) Rate of (f) = Rate of original; the surface area of the white solid appears to be the sam
Exercise 1.6.4:
At the very start of the reaction, the concentrations of reactants have not changed very much. That means the rate of the reaction remains roughly constant as the first few percent of reactants are consumed. Plotting [product] vs. time gives a straight line with the slope = rate. However, over the course of the reaction, the concentration of reactants goes down as the reactants are consumed. That means the rate of product formation slows down and a plot of [product] vs. time becomes curved. We will be unable to measure the slope in a simple way.
Exercise 1.6.5:
The slope of the first curve, with [A]o = 1 mol L-1, can be estimated by observing that [C] increases from zero to 25 mmol L-1 in 50 seconds. The slope is about \(\frac{25}{50} = 0.5 \frac{mmol}{Ls}\). The slope of the next curve, with \([A]_{0} = 2 \frac{mol}{L}\), is \(1.0 \frac{mmol}{Ls} (\frac{50 \frac{mmol}{L}}{50s})\). The initial concentration is doubled, and the rate doubles. The slope of the final curve, with \([A]_{0} = 4 \frac{mol}{L}\), is \(2.0 \frac{mol}{Ls} (\frac{100 \frac{mmol}{L}}{50s})\). The initial concentration is doubled, and the rate doubles. The reaction is linearly dependent on the concentration of A. Whatever happens to [A] also happens to the rate.
In terms of rate laws, there is a mathematical approach to demonstrating this relationship.
Suppose \(Rate = k[A]^{x}\); x is the power of the mathematical relationship.
The ratio of rates in two experiments is \(\frac{Rate_{1}}{Rate_{2}} = (\frac{k[A_{1}]^{x}}{k[A_{2}]^{x}}) = (\frac{[A_{1}]}{[A_{2}]})^{x}\)
If we take the logarithm of both sides: \(\ln (\frac{Rate_{1}}{Rate_{2}}) = \ln ((\frac{[A_{1}]}{[A_{2}]})^{x}) = x \ln (\frac{[A_{1}]}{[A_{2}]})\)
Then \(x = \frac{ln(\frac{Rate_{1}}{Rate_{2}})}{ln(\frac{[A_{1}]}{[A_{2}]})}\)
Exercise 1.6.6:
- Each time the concentrations double (for example, from 2 to 4 mol L-1), the rate quadruples (for example, from 50/50 = 1 mmol L-1 s-1 to 200/50 = 4 mmol L-1s-1). One explanation is Rate = k[A][B].
- Another explanation is \(Rate = k[A]^{2} \: or \: Rate = k[B]^{2}\)
- We could run a series of experiments in which [A] is changed while holding [B] constant (or vice versa).
Exercise 1.7.1:
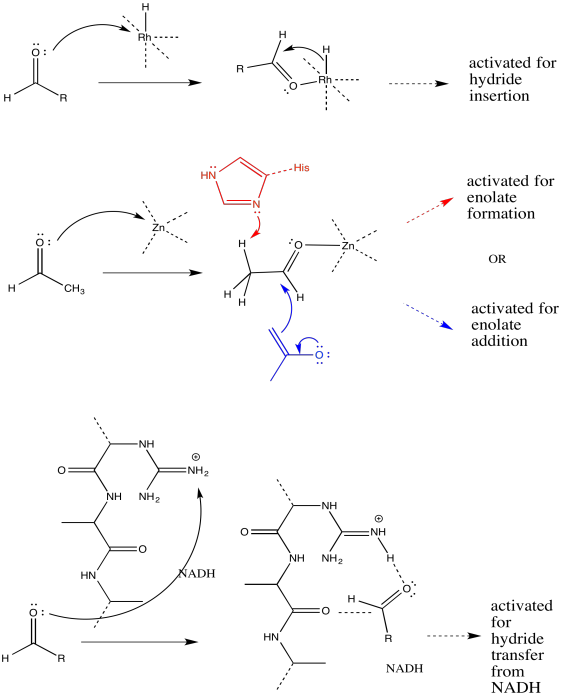
a)

b) The first step proceeds at k1; the second at k2.
c) The second step is probably reversible. It is just the exchange of a proton from one OH group to another.
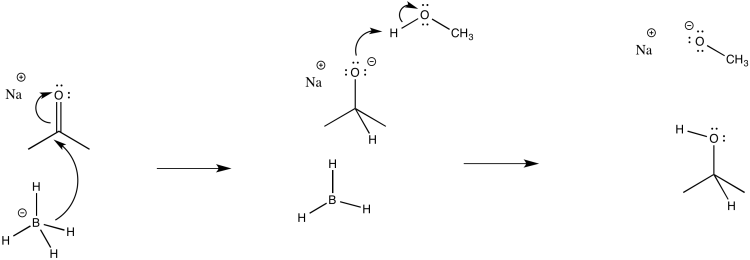
d)
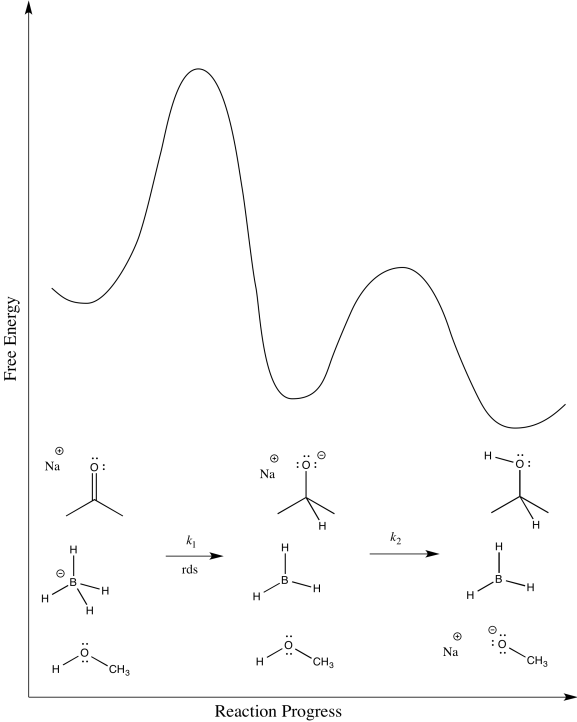
e) \(Rate = k_{1} [ketone][NaBH_{4}]\)
Exercise 1.7.2:
a)
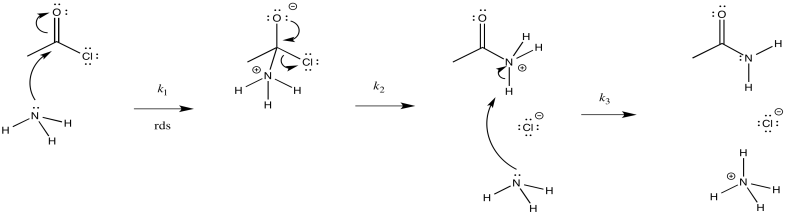
b) The first step proceeds at k1; the second at k2; the third at k3.
c) There are three different steps, each of which might be rate determining.
The first:

The second:
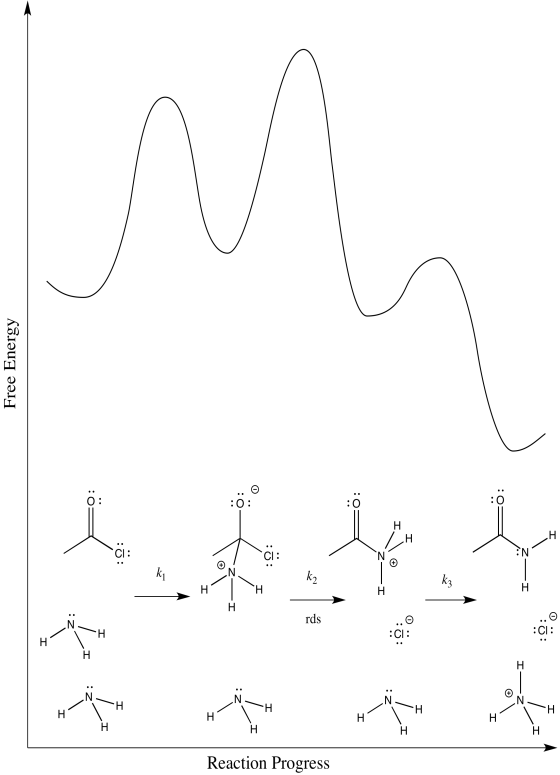
The third:
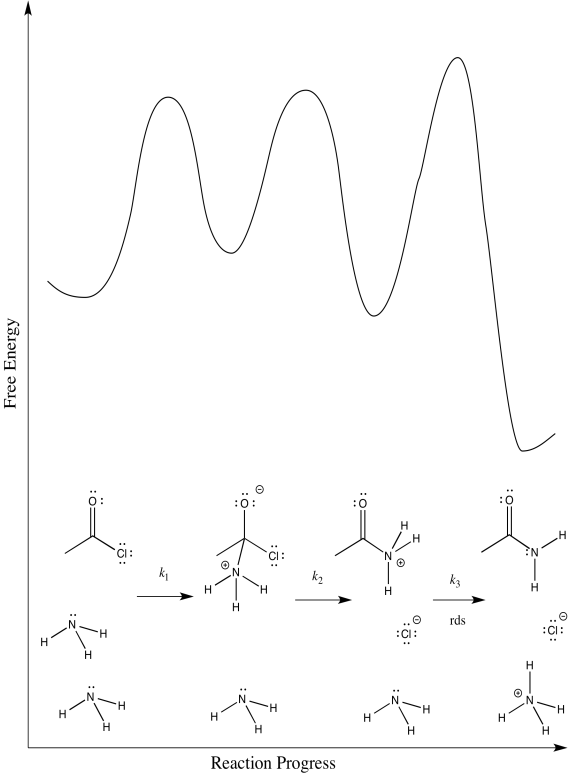
d) First one: \(Rate = k_{1}[CH_{3}COCl][NH_{3}]\)
Second one: \(Rate = k_{1}k_{2}[CH_{3}COCl][NH_{3}]\)
Third one: \(Rate = k_{1}k_{2}k_{3}[CH_{3}COCl][NH_{3}]^{2}\)
The rate law could be used to distinguish the third from the first two. However, it would be impossible to tell the difference between the first two using the rate law alone.
e) We can probably rule out the third possibility right away. Proton transfers tend to happen pretty quickly, especially in the presence of a reasonable base such as ammonia. Measuring the rate law would quickly confirm this assumption.
Scenarios 1 and 2 are much harder to distinguish. In both cases, a bond is being broken as another bond is being made. We could make an educated guess that the formation of the good chloride leaving group is pretty easy; that would make step 1 the rate determining step.
However, we are always left with some ambiguity in subtle cases like this one. In order to get a better idea about which transition states are the highest, we would have to perform computational chemistry.
Exercise 1.7.3:
a) i)
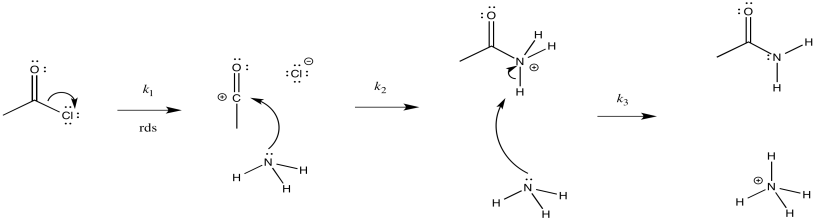
ii)

iii) \(Rate = k_{1}[CH_{3}COCl]\)
b) i)
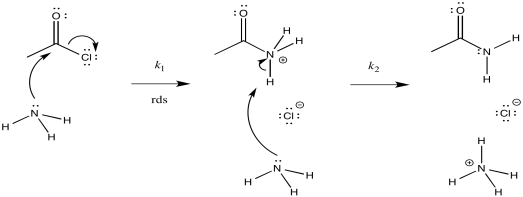
ii)
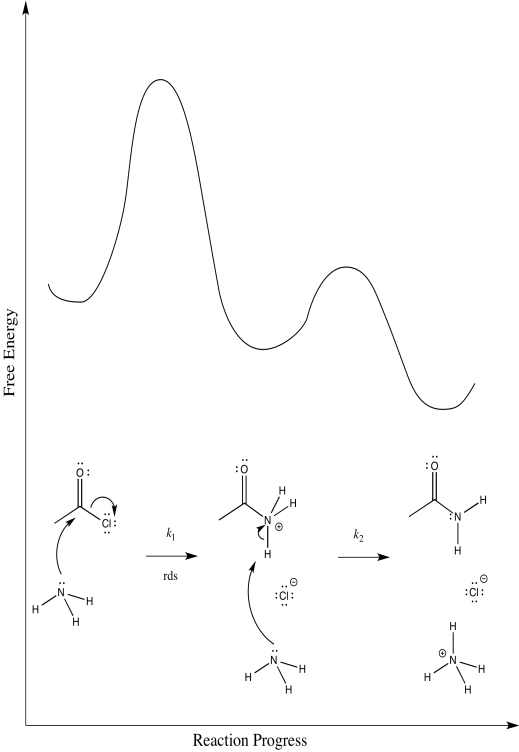
iii) \(Rate = k_{1}[CH_{3}COCl][NH_{3}]\)
c) On the basis of the rate law, possibility (a) can be ruled out, but not possibility (b)
Exercise 1.7.4:
- There is a geometry change prior to or during the rate determining step.
- Possibility (b) can be ruled out.
Exercise 1.7.6
a)
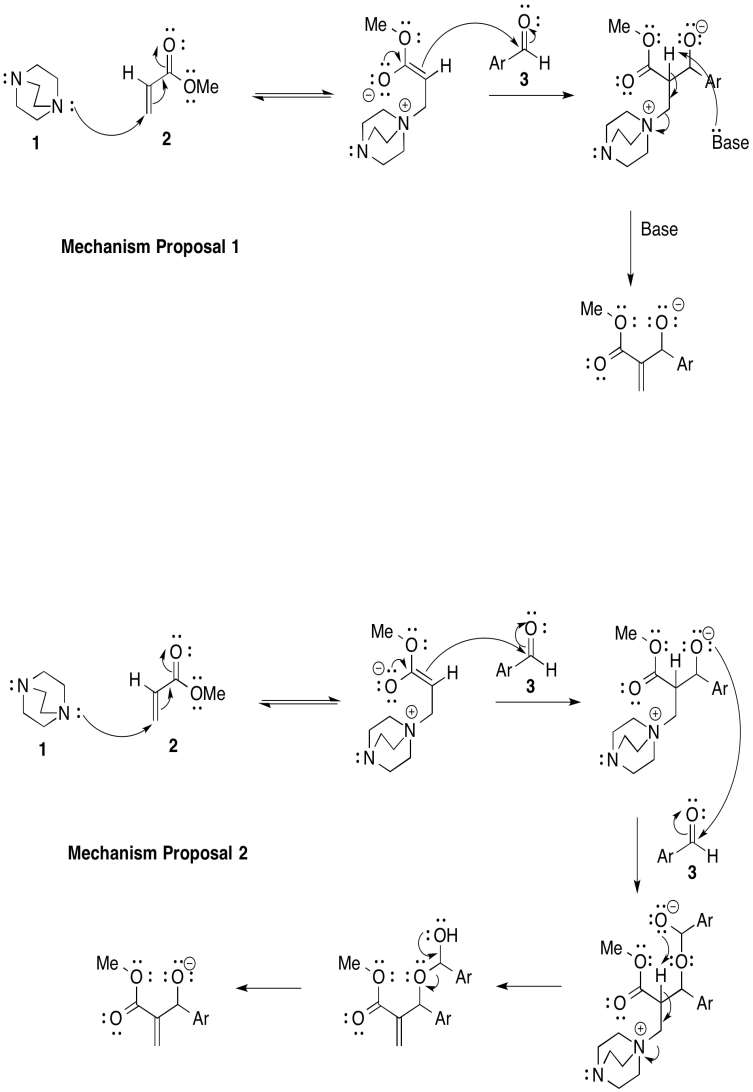
b) Mechanism 1: \(k[1][2][3]\)
Mechanism 2: \(k[1][2][3]^{2}\)
c) First order in [1]; first order in [2]; second order in [3]
d) Mechanism 2.
Exercise 1.8.2: