8.8: Thermodynamics of Glycolysis
- Page ID
- 200188
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Glycolysis is intimately linked to the release of energy in biological systems, and harnessing that energy to do work. That's what the field of thermodynamics is all about. In this section, we will take a very brief look at some of the energetic considerations of this pathway.
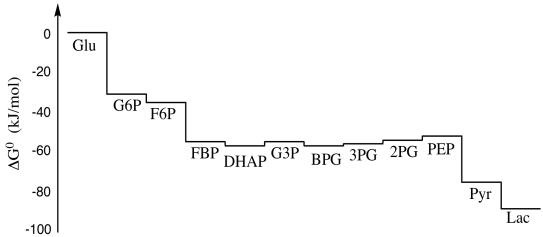
We have seen that glycolysis is a sequence of reactions leading from one intermediate compound in the pathway to the next. (To see that pathway again, click here.) Inevitably, there are energy changes associated with each of those reactions. Some of the reactions may be endothermic, others may be exothermic; some may be essentially irreversible, whereas others may occur in equilibrium. If we map these energy changes out from start to finish, we get a picture like the one below. It's a roller coaster, with lots of energetic drops but just as many hills, and it becomes difficult to think of glycolysis as a process that releases energy, except for the dramatic drop in the last couple of steps.
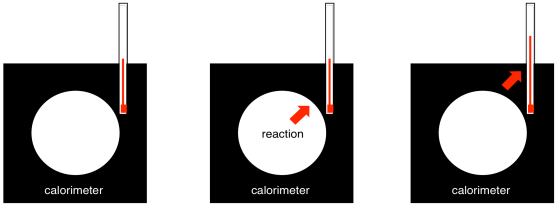
Where does a picture like this one come from? Well, it depicts a series of reactions, and the energy change associated with each reaction. We can determine the energy change associated with a specific reaction using calorimetry. A calorimeter is a well-insulated device in which we can perform a reaction. A thermometer tells us the temperature change as a result of the reaction. We can calibrate the device by releasing known amounts of heat and seeing how much its temperature rises. Consequently, we can also use that correlation backwards: given the temperature rise, we can deduce how much energy was released during a reaction.
Now, if enough people have studied this sort of thing for long enough, we can begin to compile a lot of data. Given enough data, you actually might not need to perform calorimetry to determine how much energy is involved in a reaction.
To illustrate why, consider one of the most common kinds of thermodynamic data you can find: heats of formation. The heat of formation of a compound is the energy involved when the compound is formed from the elements. So, for example, the heat of formation of methane would be the energy involved when hydrogen cas combines with carbon to form methane:
\[\ce{2H2 + C -> CH4 \: \: \Delta H = ??} \nonumber\]
It would be difficult to perform calorimetry in this case. First of all, there are just too many things that could happen if you managed to get hydrogen and carbon to combine; there are many other compounds made from hydrogen and carbon, so who knows what reaction would really occur?
But we find that heat of formation indirectly, using other data. We can burn methane:
\[\ce{2O2 + CH4 -> CO2 + 2H2O \: \: \Delta H = -802 \frac{kJ}{mol}} \nonumber\]
We can burn hydrogen to get water:
\[\ce{H2 + 0.5 O2 -> H2O \: \: \Delta H = -285_{.}8 \frac{kJ}{mol}} \nonumber\]
We can burn carbon to get carbon dioxide:
\[\ce{O2 + C -> CO2 \: \: \Delta H = -393_{.}5 \frac{kJ}{mol}} \nonumber\]
Well, that just seems like a series of random facts, but equations of reaction are quite a bit like algebraic equations, and those reaction arrows are quite a bit like equals signs. If we keep that in mind, we can manipulate these equations to get useful information. For example, what would happen if we took the middle reaction and multiplied it by two?
\[\ce{2H2 + O2 -> 2H2O \: \: \Delta H = -571_{.}6 \frac{kJ}{mol}} \nonumber\]
Just as in algebra, if we multiply every term in an equation by the same factor, we end up with an equivalent equation. It's a perfectly legal operation. Note that if we multiple the equation by two, we also multiply the energy by two; it's part of the equation.
Now, you probably already know what happens if we consider one of these equations in reverse:
\[\ce{2CO2 + 2H2O -> 2O2 + CH4 \: \: \Delta H = +802 \frac{kJ}{mol}} \nonumber\]
If the reaction is exothermic in one direction, then it must be endothermic in the other. One way is downhill, so the other way is uphill.
Look what happens if we add these three reactions together in their current forms:
\[\ce{CO2 + 2H2O -> 2O2 + CH4 \: \: \Delta H = + 890_{.}3 \frac{kJ}{mol}} \nonumber\]
\[\ce{2H2 + O2 -> 2H2O \: \: \: \: \: \: \: \Delta H =-571_{.}6 \frac{kJ}{mol}} \nonumber\]
\[\ce{O2 + C -> CO2 \: \: \: \: \: \: \: \Delta H = -393_{.}5 \frac{kJ}{mol}} \nonumber\]
\[\ce{CO2 + 2H2O + 2O2 +2H2 + C -> 2O2 + CH4 + 2H2O + CO2 \: \: \Delta H = +802 \frac{kJ}{mol}} \nonumber\]
Several things cancel on the left and right, leaving:
\[\ce{2H2 + C -> CH4 \: \: \Delta H = -74_{.}8 \frac{kJ}{mol}} \nonumber\]
What that means is that, if we have energetic information about some reactions, and we can combine the equations for those reactions to get a new equation of reaction, then we automatically get the energy associated with that new reaction.
Essentially, if we want to know about the energetics of producing methane from carbon and hydrogen, then it doesn't matter how we get from the carbon and the hydrogen to the methane. We can first take the carbon and combine it with oxygen, not hydrogen, and make carbon dioxide. Then, we can take hydrogen and combine it with oxygen, not carbon, to make water. If, finally, we combine the water and the carbon dioxide we have made and produce methane, then the energy of that whole, roundabout process is the same as if we converted the carbon and the hydrogen directly into methane.
This idea illustrates something called Hess' Law. The overall energy required to get from one set of reactants to another set of products is always the same, regardless of the path taken. Hess' Law is true because energy is a "state function". If we know the state that something is currently in - for example, methane in the gas phase at a certain temperature and pressure - then we know its energy. It doesn't matter what has happened to it before, or how it got to its current state.
Problem GL9.1.
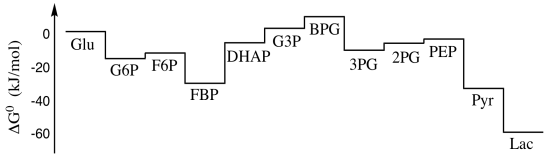
In the next section, we are going to see a slightly different picture of the energetic terrain of glycolysis. Rather than the roller coaster ride we saw before, we will find that glycolysis exists mostly on an energetic plain, with just a couple of steep drops. The reason for that has to do with the relative concentrations of the different species under cellular conditions.