5.4: Solutions For Selected Problems

Exercise 5.1.1:

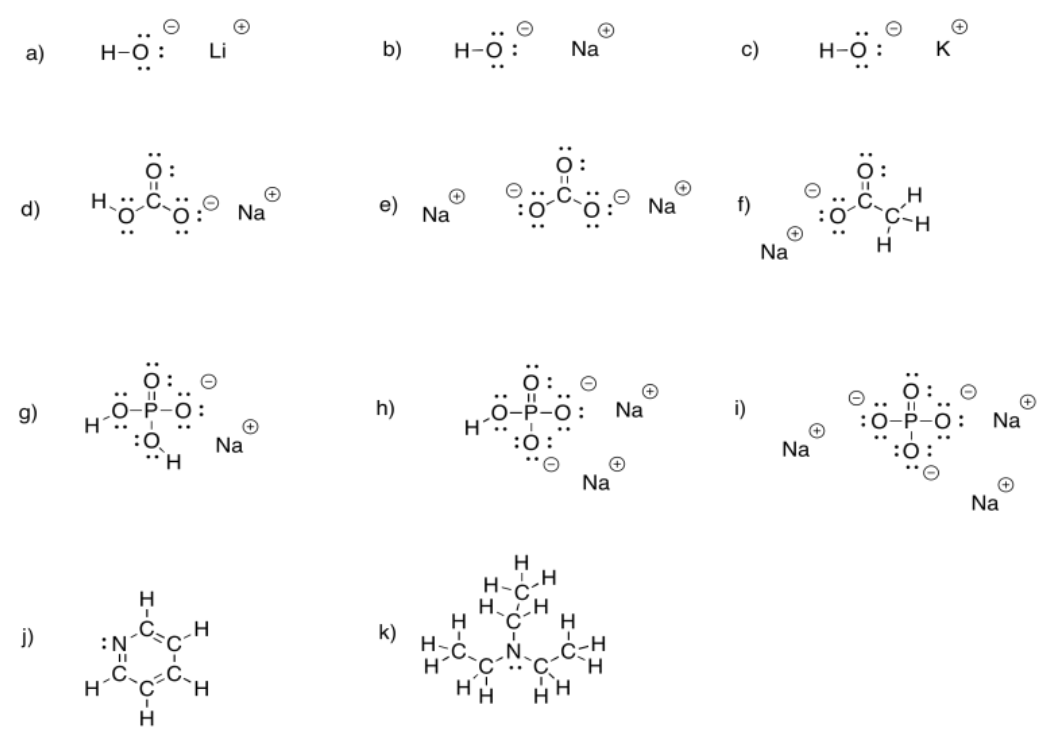
These heteroatoms are all found in the upper right-hand corner of the periodic table. They are all pretty electronegative and they all have lone pairs.

Exercise 5.2.2:

1. The electronegativity of the heteroatom attached to the carbonyl group in a carboxyloid is one factor that allows it to leave and form its own stable anion.
2. Although carbon and hydrogen are more electronegative than many of the elements in the periodic table, they are not stable enough as anions to form easily on their own.

Exercise 5.2.3:

Exercise 5.2.4:

Exercise 5.3.1:

We might expect carboxyloids with the most electronegative elements attached to the carbonyl to be the most reactive and least stable towards substitution (in other words, carboxyloids with the most electronegative heteroatoms would become substituted the most easily).

In that case, we would predict that the carboxyloids with the most electronegative substituent (oxygen) would be the most reactive. There are a number of different kinds and we will think about how they relate to each other shortly.

After the oxygen derivatives we would predict either the nitrogen derivatives or the chloride, depending on what electronegativity scale we happen to use (remember, electronegativity is not an experimentally pure property, but the result of a calculation that can be performed in different ways). The sulfur derivative would be least reactive.

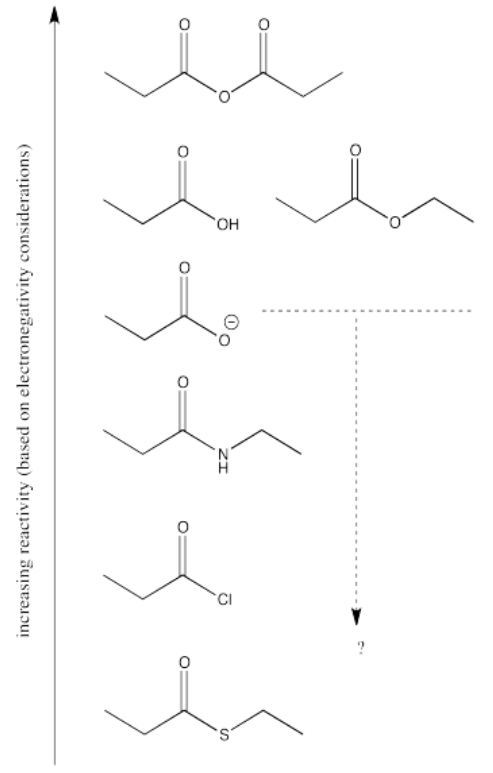
There are still several different oxygen derivatives to compare: carboxylic acids (OH), carboxylates (O-), esters (OR, in which R is an alkyl or carbon chain) and acid anhydrides (OC=O). The easiest to differentiate is the carboxylate, because of its negative charge. It must be less attractive to a nucleophile than the other oxygen derivatives, because it would offer more repulsion to an incoming lone pair.

However, we can't really predict whether it would be any less reactive than the nitrogen, chlorine or sulfur analogues, because who knows whether the charge or the nature of the atom matters more?

As it happens, the charge probably matters more. We learn that simply by looking at the experimental trend and seeing that the carboxylate is the least reactive of all the carboxyloids.

Turning to the other three oxygen derivatives, it would be difficult to differentiate between the effect of a remote hydrogen atom versus an alkyl chain in the ester versus the carboxylic acid, so we'll say those two are about the same. On the other hand, the additional electron-withdrawing carbonyl group in the acid anhydride probably has a profound effect, so we would expect that compound to attract nucleophiles more strongly.

Of course, the series we have produced above is not the "right answer". It does not match the experimentally observed series of carboxyloid reactivities. Nevertheless, it is very useful in terms of building an understanding of carboxyloids. It tells us that electronegativity may play a role here, but that it can't be the only factor.

Some other factor is putting some of the derivatives out of order. In particular, the acid chloride (C=OCl) and the thioester (C=OSR) do not fit.

Exercise 5.3.2:

Electronegativity is an abvious factor that could influence an atom's ability to π-donate, but we just looked at that factor in the previous section, so let's look at another atomic property instead. Of course, different atoms have different sizes. In particular, if we look at the atoms involved in carboxyloid substituents, we can divide them into 2nd row atoms and 3rd row atoms.

It's actually well-documented that the degree of overlap between two orbitals influences how well they bond together. Since carbon is in the second row, it is about the same size as, and overlaps pretty well with, other second row atoms. Third row atoms are a little too big, on the other hand.

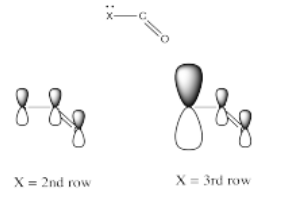
That factor breaks the carboxyloids into two different groups. Assuming π-donation is a major factor, sulfur and chlorine may be placed above the others in tems of reactivity. They cannot donate as well as oxygen or nitrogen can.

From there, differences among the atoms from the same row may be sorted out based on electronegativity differences.

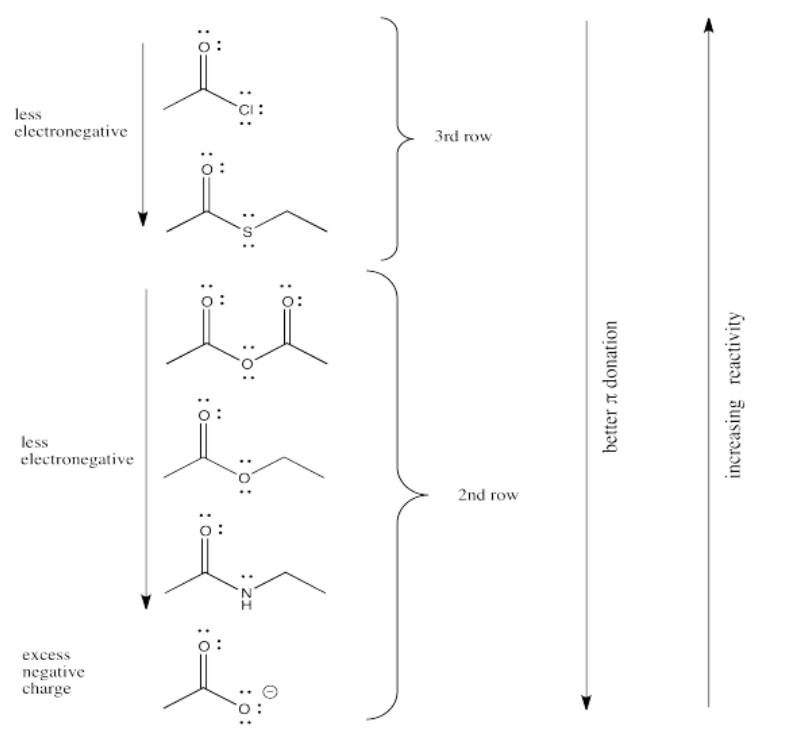
Exercise 5.3.3:

Amide bonds are among the most stable carboxyloids possible. That stability makes them well-suited to form useful structures that will not decompose easily. Remember, any change that occurs in matter occurs through chemical reactions, including the formation and decomposition of biomaterials. Shutting down a potential chemical reaction means a material will be more durable.

Exercise 5.3.4:

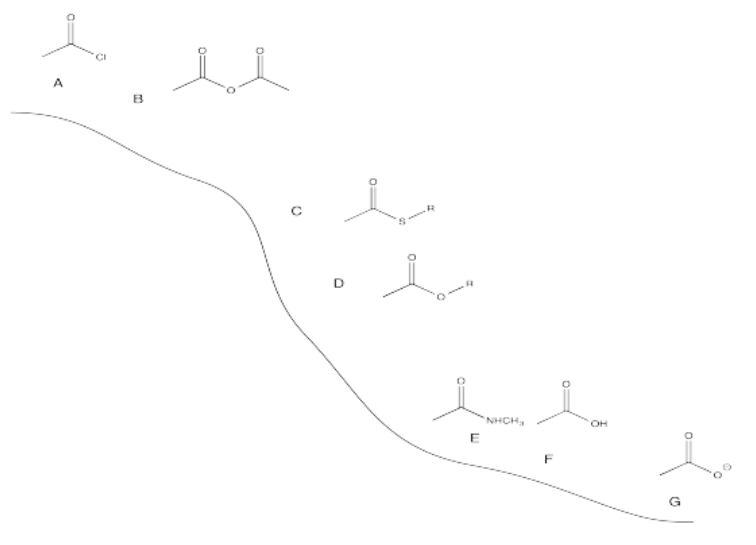
Exercise 5.3.5:

One possibility is the presence of an additional electronegative substituent. In the oxalyl chloride, the presence of an additional carbonyl next to the electrophilic acid chloride group would make each carbonyl even more electrophilic. In the thionyl chloride, the presence of two chlorines, instead of just one, could make this compound much less stable and more electrophilic.

Exercise 5.4.1:

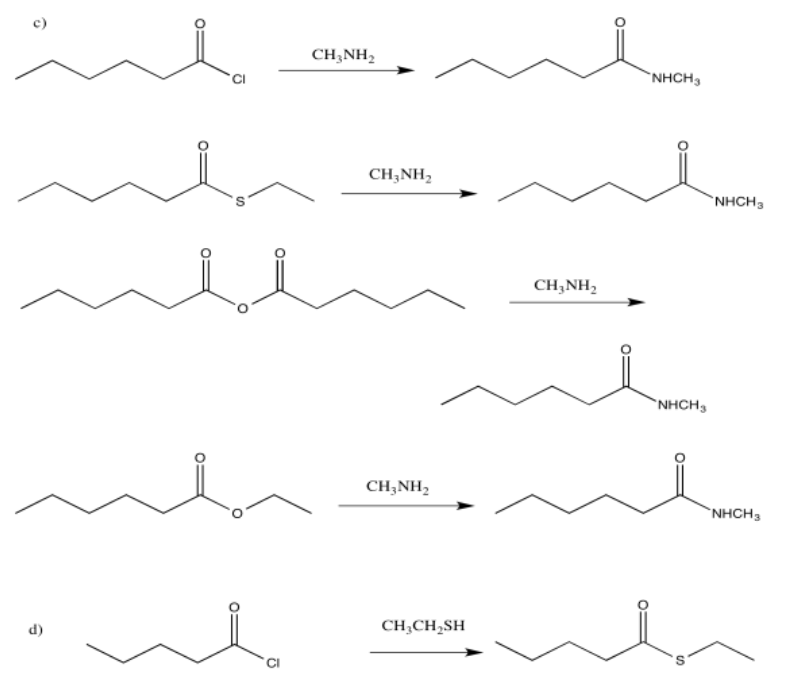
Exercise 5.4.2:

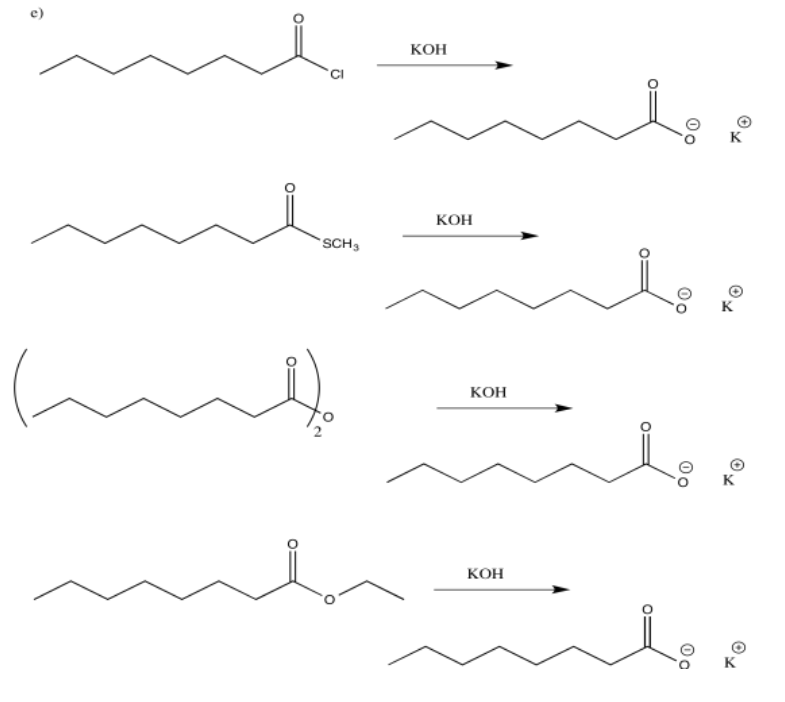
Exercise 5.4.3:

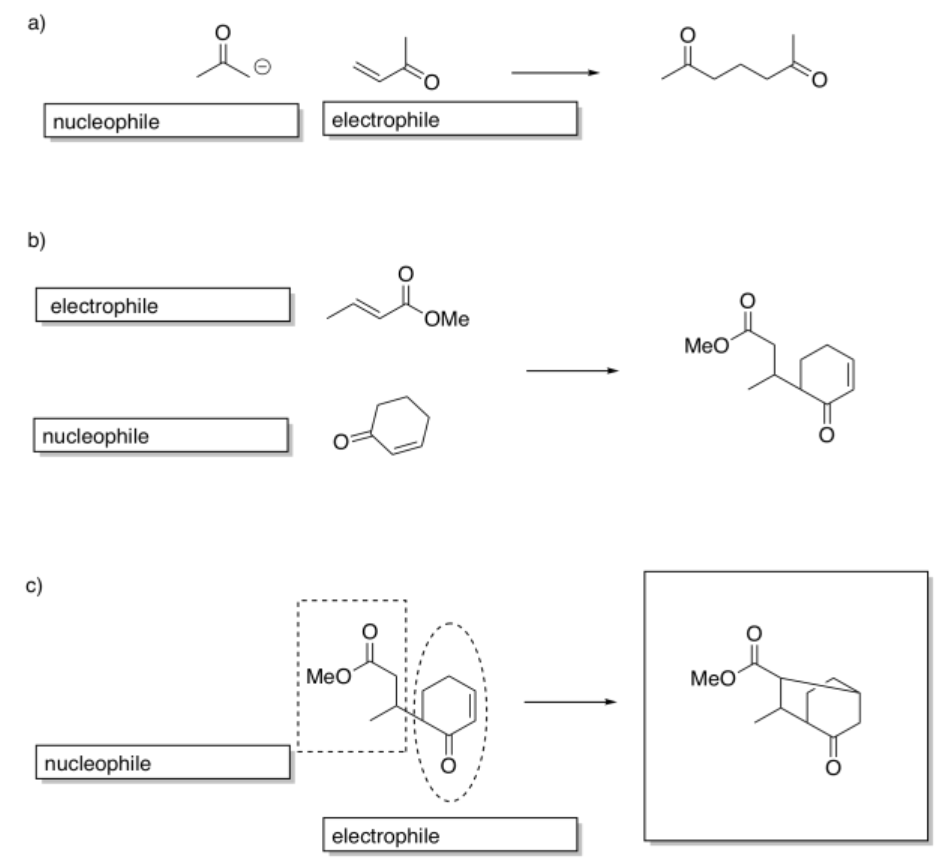
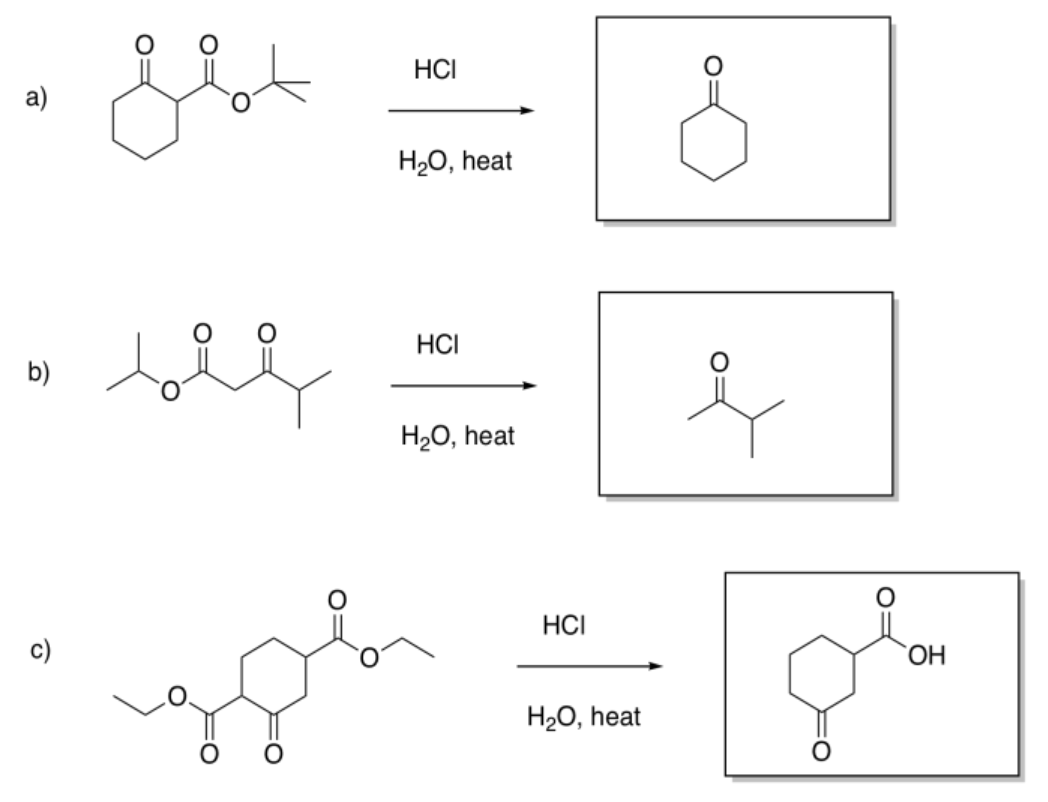
a)

b)

Exercise 5.4.4

Exercise 5.4.5:

Exercise 5.4.6:

Exercise 5.4.7:

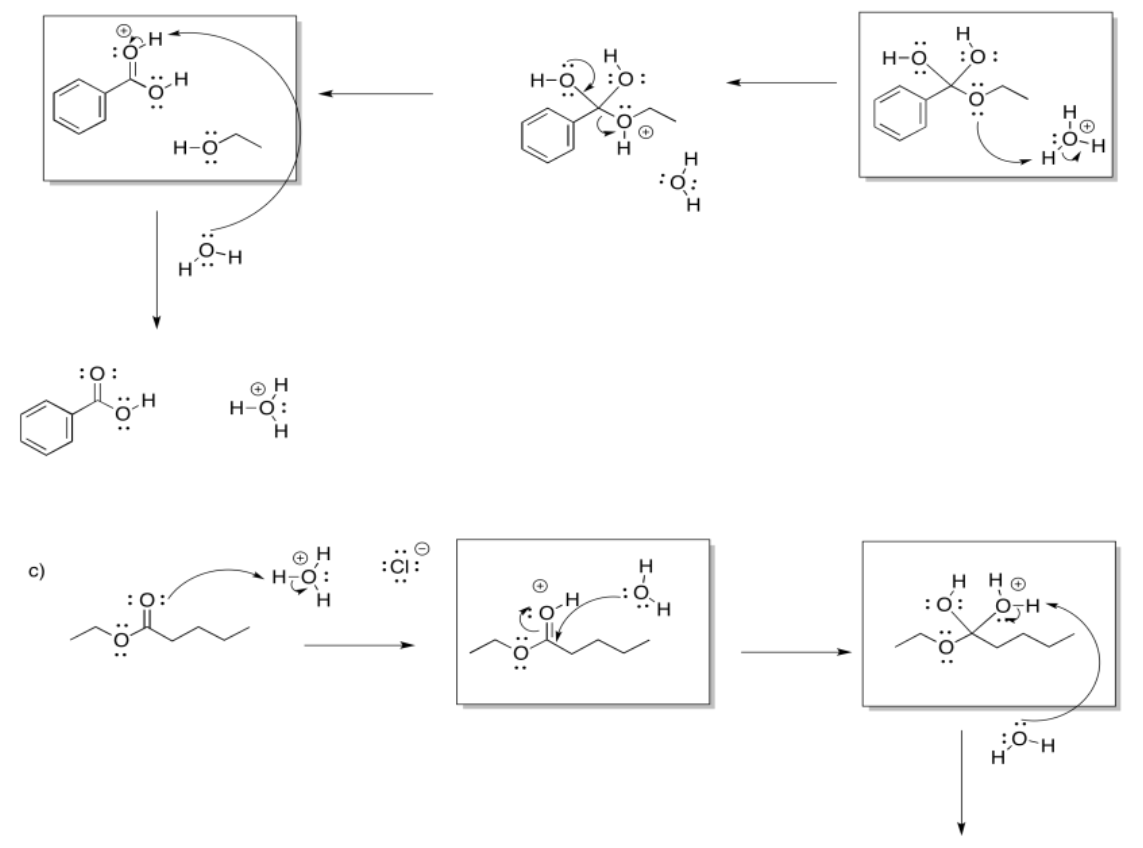
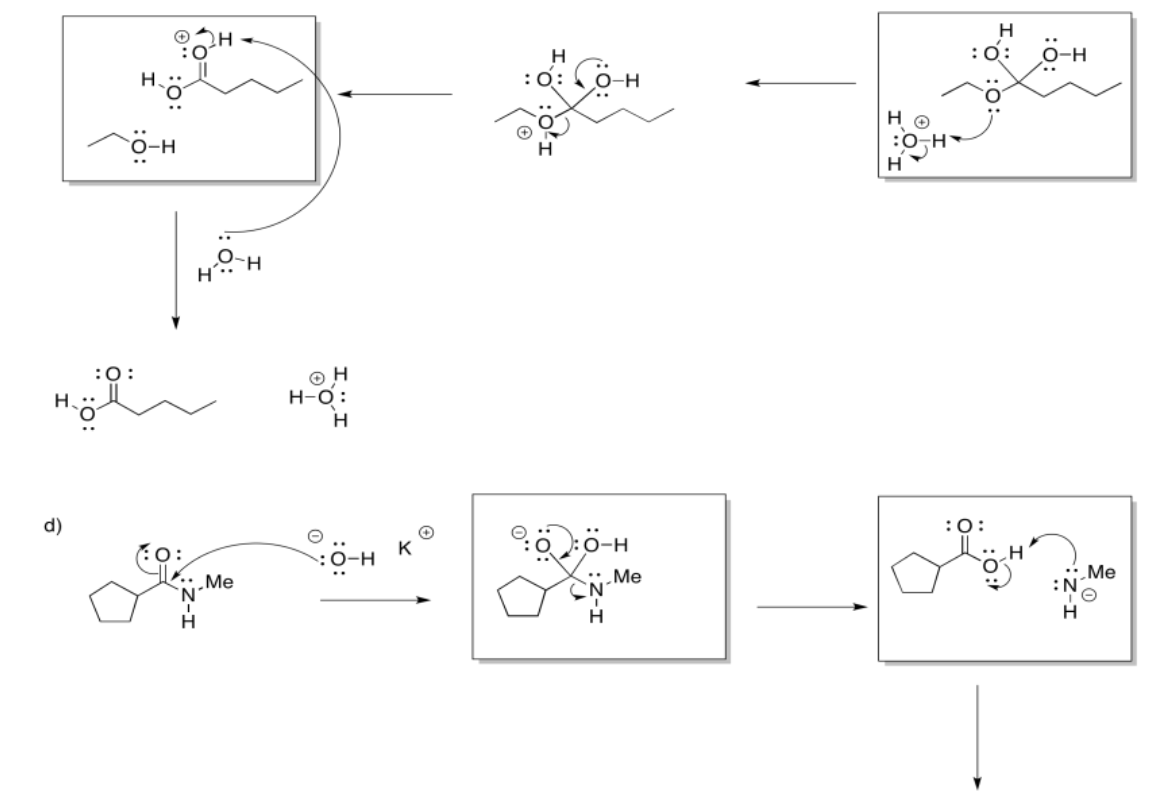
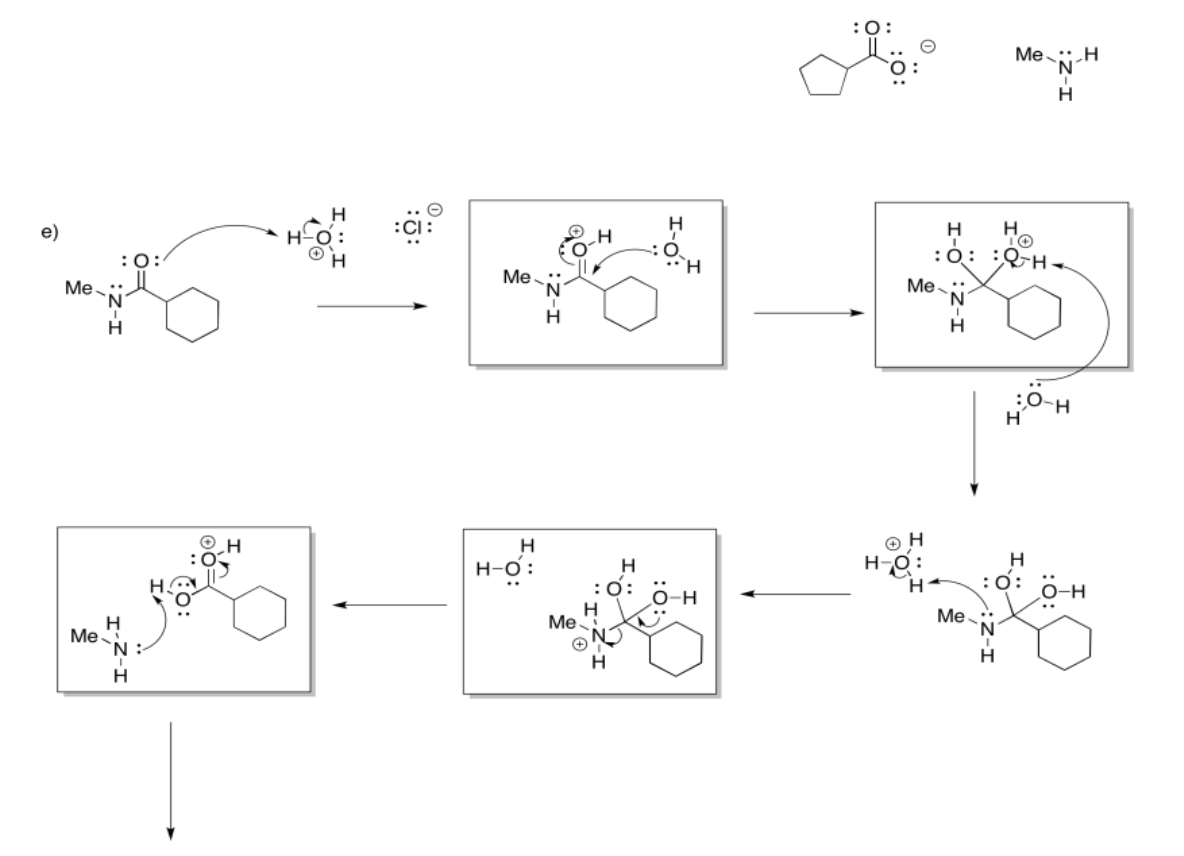
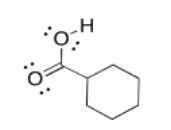
Exercise 5.5.4:

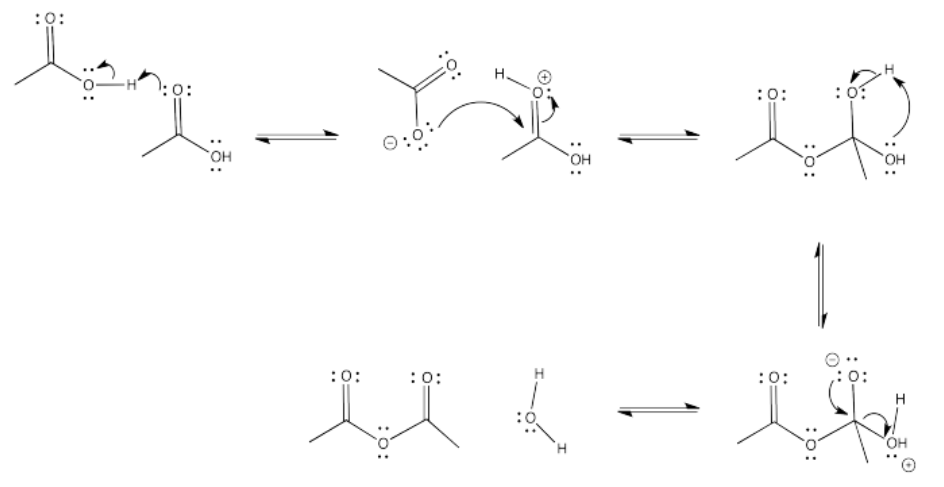
Exercise 5.5.8:

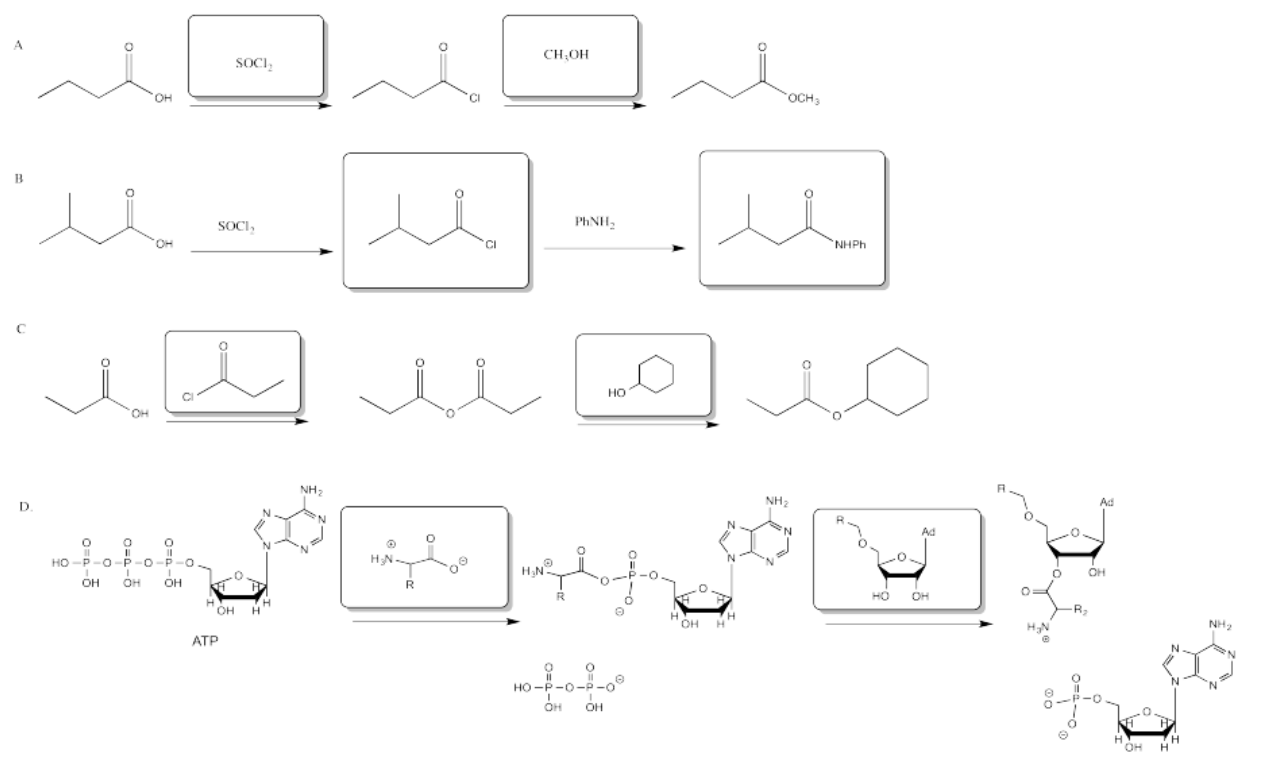
Exercise 5.6.1:

Because acid chlorides are at the top of the carboxyloid reactivity diagram (the ski hill), and other halides are likely to be similar in reactivity to the chloride, this reaction would be uphill from the other carboxyloids.

Exercise 5.6.4:

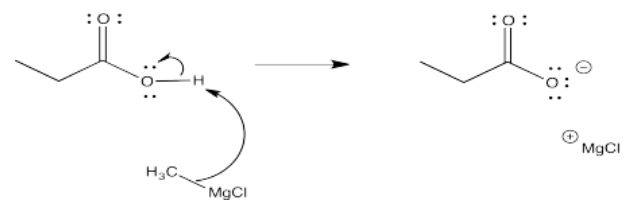
Exercise 5.6.5:

Amides and carboxylates are the least reactive carboxyloids, so it might not be too surprising that they do not react with these nucleophiles.

Exercise 5.6.6:

Acid chlorides typically react with these cuprate reagents.

Exercise 5.6.7:

Borohydrides could presumably react with acid chlorides, anhydrides and thioesters, which are the most reactive carboxyloids. They probably can't react with amids or carboxylate ions, which are even farther downhill than esters.

Exercise 5.6.11:

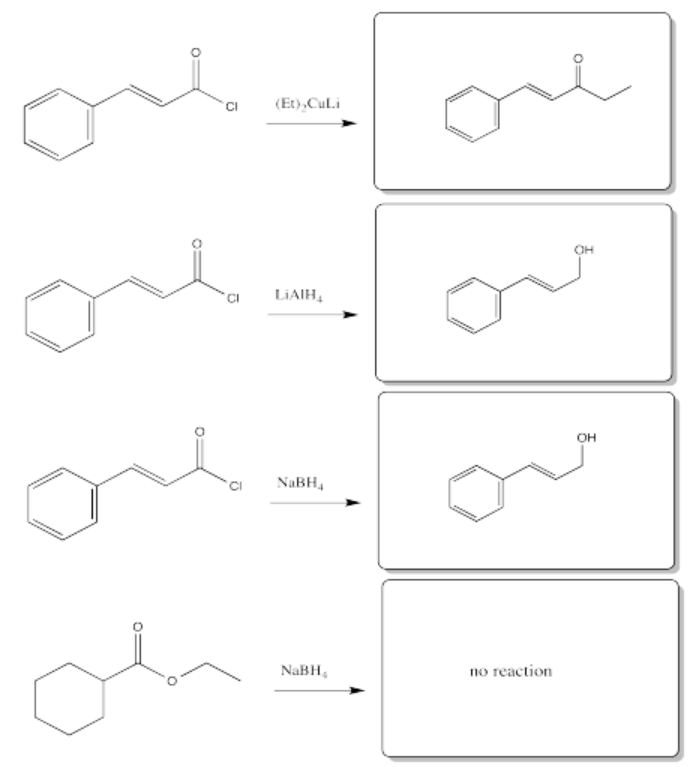
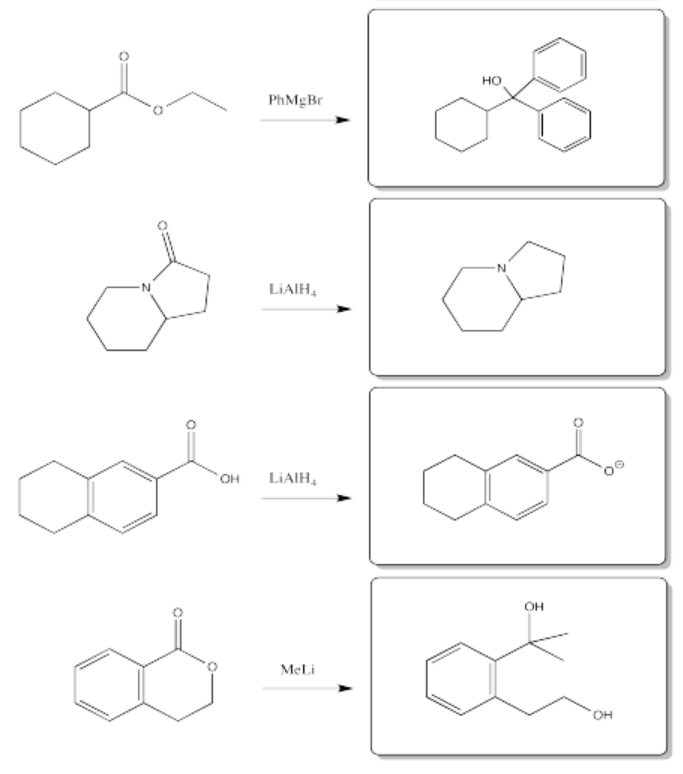
Exercise 5.7.1:

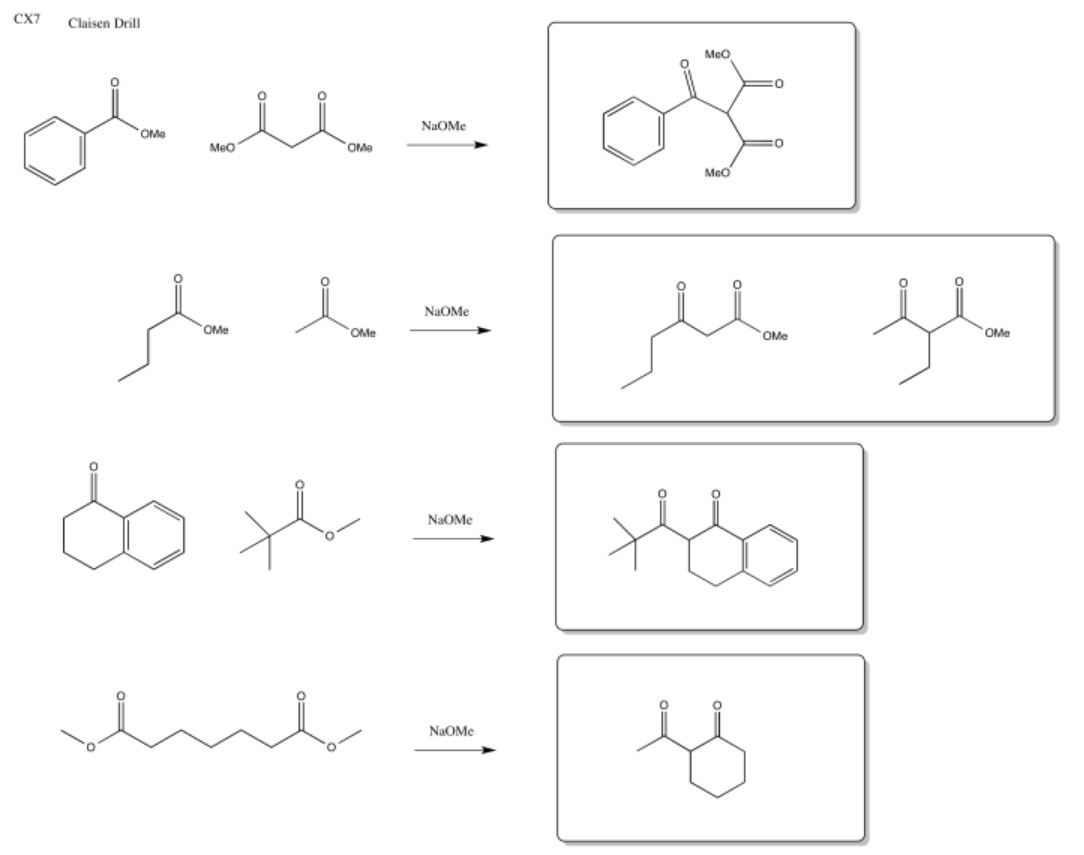
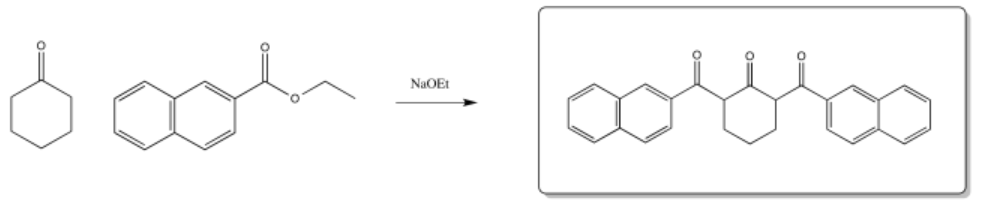
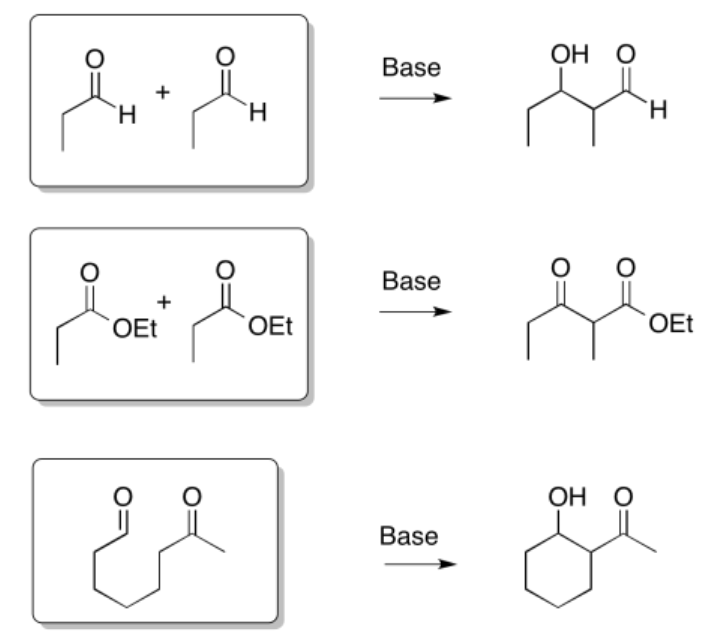
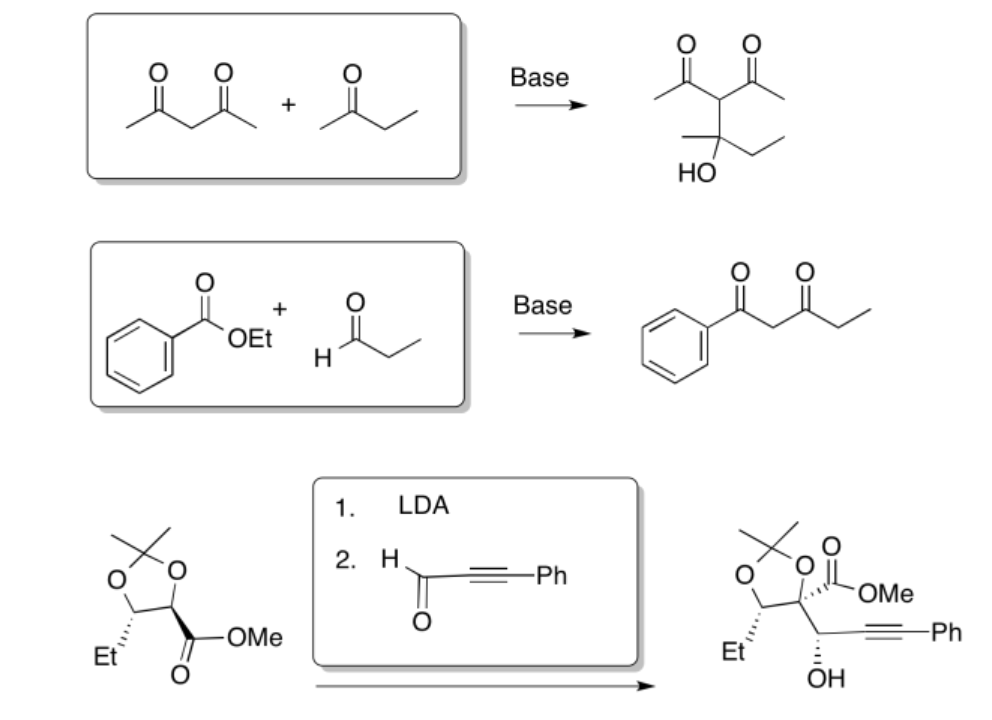
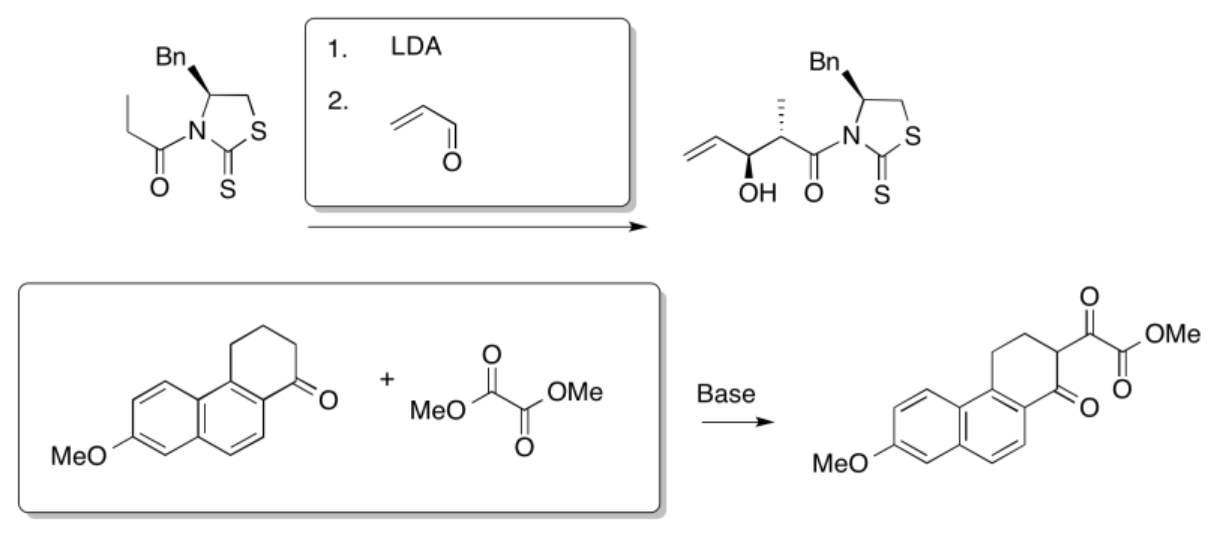
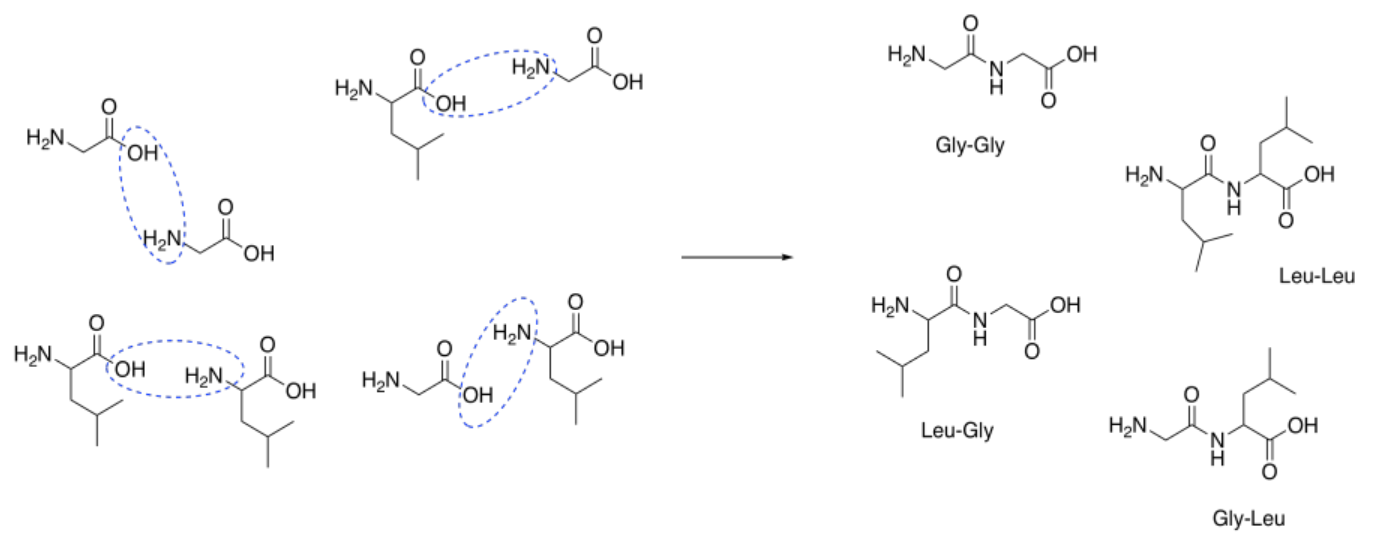
That combination would give thw following dipeptides:

ala-ala ala-gly ala-val

gly-gly gly-ala gly-val

val-val val-ala val-gly

Of course, we might also get tripeptides, such as ala-ala-gly-val, and so on.

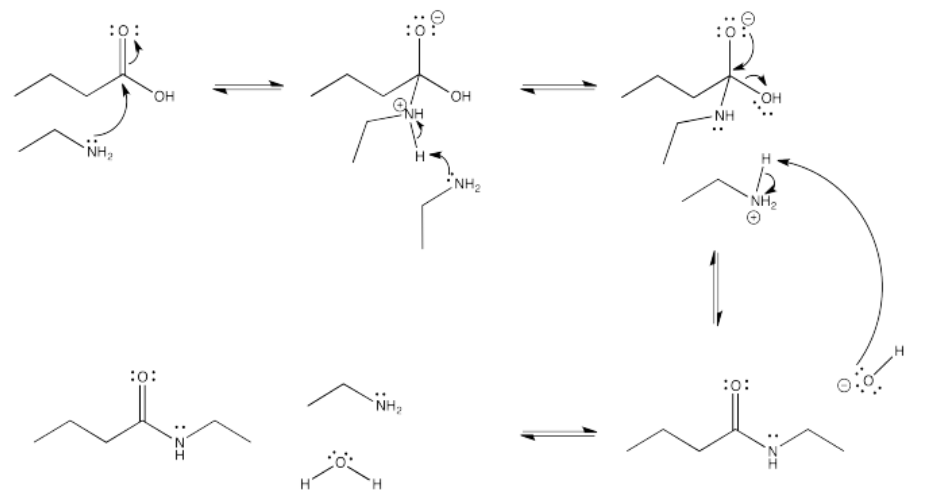
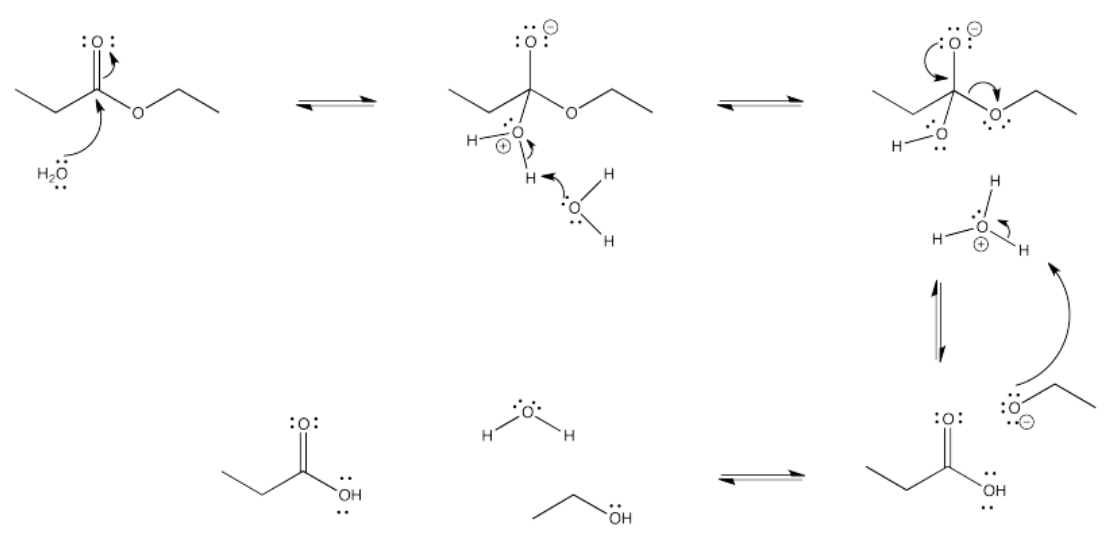
Carboxylic acids usually require activation before they can act as nucleophiles. That problem is actually complicated here because the carboxylic acid is in equilibrium with a carboxylate salt (read further on the page).

The relative reactivity of carboxyloids results from a balance between sigma electron withdrawing effects and pi-donation. An electronegative atom attached to a carbonyl tends to withdraw electron density, making the carbonyl even more positive and electrophilic. On the other hand, pi-donation from a neighbouring atom with a lone pair actually lowers electrophilicity by forming a stable, conjugated system.

In a carbamate, an additional electronegative atom is added to the carbonyl: it has an oxygen as well as a nitrogen adjacent to the C=O group. That atom draws electron density away from the carbonyl, making it more electrophilic. However, pi-donation from the additional oxygen does not result in a more stable conjugated system. The maximum pi system is still just three atoms long; it either involves conjugation of the O-C=O or the N-C=O unit. It does not, for example, lead to an even more stable conjugated system that is four atoms long.

As a result, the added oxygen probably contributes more to the electron-withdrawing effect than it does to stabilisation of the pi system.

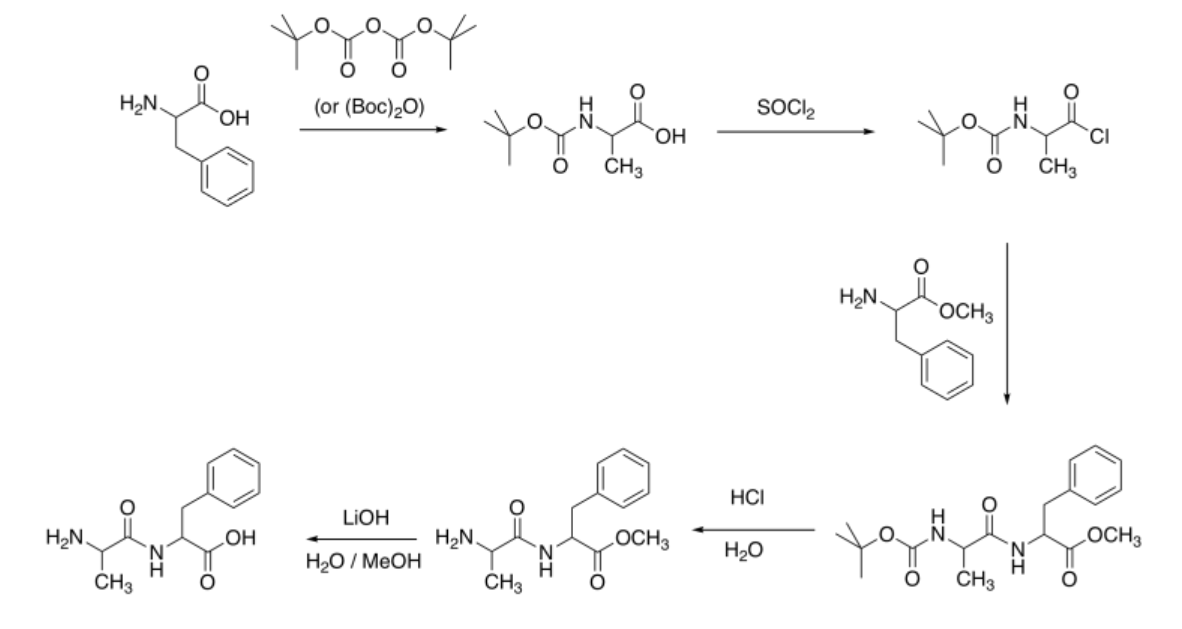
The more polar hydrochloride salt of EDCI is often used, as pictured. This more polar compound dissolves well in polar solvents, such as water, that also dissolve amino acids.

One can also imagine the amino group in EDCI acting as a site for catalysis, shuttling protons from one place to another.

Problem CX10.1.

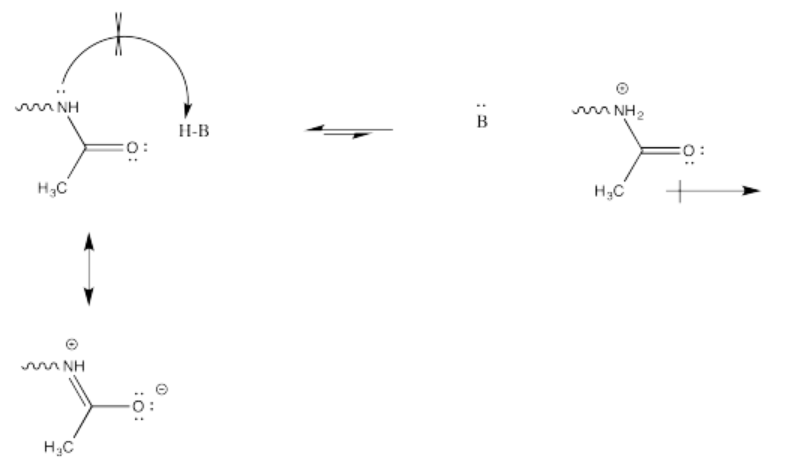
This change in charge results because, although amines are easily protonated, amides are not. Protonation of an amide would result in a cation adjacent to the very positive carbonyl carbon, leading to a buildup of localized positive charge. That wouldn't be easy. Furthermore, the amide nitrogen is not very likely to donate its electrons to a proton in the first place. Its protons are too busy. They are tied up in conjugation with the carbonyl, so they really aren't available to act as the lone pair of a base.