3.14: Conjugate Addition
- Page ID
- 195903
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Conjugated systems are structures that contain alternating double and single bonds (or, in some cases, a double bond that is next to an atom with either a lone pair or a vacant orbital). Conjugated systems are usually at lower energy than regular double bonds because the electrons involved in bonding are delocalized; they are spread out over a greater area and thus can have a longer wavelength.
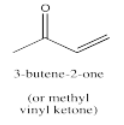
For example, the -bonding system for 3-butene-2-one (or methyl vinyl ketone) is described by orbitals involving both the carbonyl group and the alkene group. These two groups become linked together so that there is not longer an independent carbonyl nor an independent alkene, but one "enone" (a term taken from the words alkene and ketone).
Because of that extra stability, it might not be surprising that conjugated carbonyls are often a little slower to react than regular carbonyls. The surprise is that conjugated carbonyls can sometimes give additional products in which addition does not take place at the carbonyl.
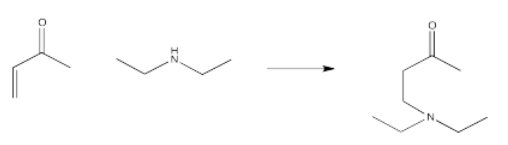
The product shown above is called a conjugate addition product, or a 1,4-addition product. In conjugate addition, the nucleophile does not donate to the carbonyl, but instead donates to an atom that is involved in conjugation with the carbonyl. This additional electrophilic position is sometimes called a "vinylogous" position (from the word vinyl, which refers to that CH=CH2 unit next to the carbonyl).
- Conjugate additions (or 1,4-additions) can occur when a carbonyl is attached to a C=C bond.
Exercise \(\PageIndex{1}\)
Draw a mechanism with curved arrows for the conjugate addition shown above.
- Answer
-
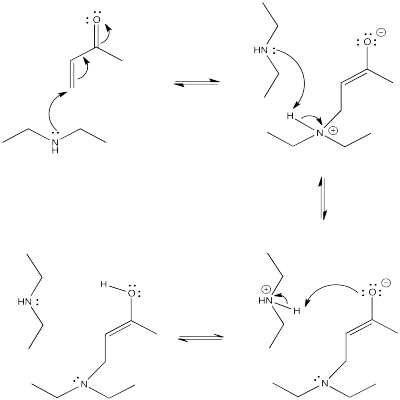
Exercise \(\PageIndex{2}\)
Regular additions to carbonyls are sometimes called 1,2-additions, whereas conjugate additions are called 1,4-additions. Show why.
- Answer
-
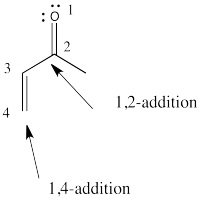
Remember that we can look at another resonance structure of a carbonyl, one that emphasizes the electron-poverty of the carbonyl carbon. It's not a good Lewis structure because of the lack of an octet on carbon, but it does reinforce the idea that there is at least some positive charge at that carbon because it is less electronegative than oxygen. Extending that idea, we can draw an additional resonance structure in a conjugated system. That third structure suggests there may be some positive charge two carbons away from the carbonyl, on the β position on the double bond.
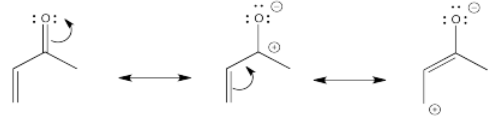
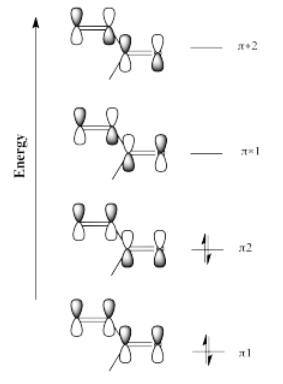
The idea that there are two electrophilic positions in an enone is reinforced by the picture of the LUMO (the lowest-energy "empty" frontier orbital, the virtual place where an additional electron would probably go). When a lone pair is donated to an electrophile, the electrons are most likely to be donated into the LUMO.
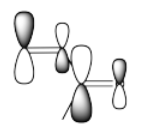
Although it isn't obvious from the cartoons we often draw for molecular orbitals, quantum mechanical calculations suggest that the LUMO is "larger" at the carbonyl position as well as the β-position on the vinyl group.
How can it be larger on some atoms than others? A molecular orbital is an algebraic combination of atomic orbitals. In this case,
\[LUMO = ap_{C1} + bp_{C2} + cp_{C3} + d_{pO} \nonumber\]
in which pC1 is the p orbital on the carbon on the left, pO is the p orbital on the oxygen, and so on. The letters a, b, c and d are just numbers; they are the coefficients in the equation. The result of the molecular orbital calculation in this case suggests that the numbers a and c are a little bigger than b and d. Incidentally, it also suggests that a and d have opposite sign from b and c (maybe a and d are positive numbers whereas b and c are negative numbers), meaning that a and d are out of phase with b and c.
In any case, we sometimes think of the large LUMO on particular atoms as being an easier "target", an easier place to throw the incoming electrons. These mathematical results really just reflect what we would expect from the resonance structures.
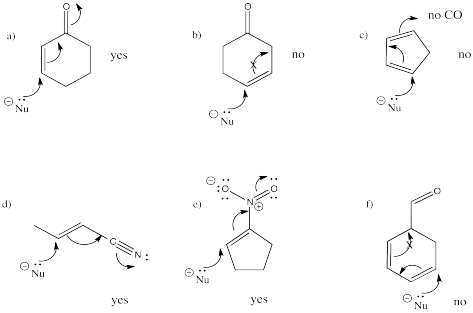
Exercise \(\PageIndex{3}\)
Indicate whether the following systems are capable of undergoing conjugate addition, and show why or why not.
- Answer
-