2.12: Jahn-Teller Distortion
- Page ID
- 195680
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lability can often be understood in terms of the d-electron count on the metal. Sometimes, there is a high-lying electron in a formally σ* orbital that destabilizes the complex and weakens a bond to a ligand. A dissociative substitution pathway may be accelerated as a result. Sometimes, there is a low-lying vacancy in a formally non-bonding level. An associative substitution pathway may be accelerated as a result.
In some cases, the d-electron count can have a subtle influence on the geometry of a complex. For example, an octahedral complex might be distorted, either stretched along one axis or else compressed. In Jahn-Teller Distortion, this effect arises from unequally-distributed electrons in the same level (degeneracy). Although this phenomenon is structural, it can sometimes exert an influence on the stability of complexes that translates into accelerated ligand substitutions.
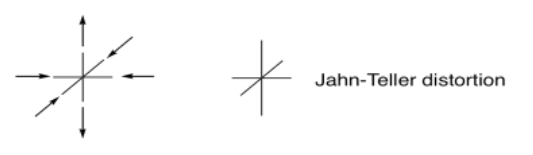
Degeneracy refers to an unequal number of electrons in orbitals at the same energy level; it is sometimes described as a situation in which there are different possible ways to fill in the electrons.

An example of this distortion can be seen in the coordination complex, (bpy)Cu(II)(hfacac)2, shown below. In this complex, one would expect the Cu-N distances to be different from the Cu-O distances. However, the two Cu-O distances should be pretty similar.
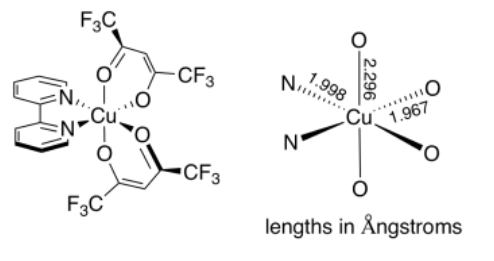
In contrast, it turns out that the two axial Cu-O distances are 17% longer than the two equatorial Cu-O distances.1 There could be different reasons for this (maybe the neighbouring nitrogen donors influence the Cu-O distances), but the main one turns out to be a Jahn-Teller effect. The same effect can be seen even in complexes such as Cu(II)(OH2)62+, in which all of the ligands are the same, but in which two of the Cu-O bonds that are trans to each other are significantly longer than the rest.
The origin of the distortion can be seen in the d orbital splitting diagram for an octahedral species. Cu(II) is a d9 ion. In its d orbital splitting diagram, the upper eg set of orbitals is unevenly occupied: one orbital contains two electrons, whereas the other contains only one. There does not appear to be anything inherently wrong with that; rather, there is simply an advantage to distortion.
Suppose the two axial ligands in the octahedron back away from the metal. Imagine that they are interacting with the dz2 orbital. Their interaction with that orbital resulted in the dz2 rising in energy because it is the dominant contributor to the σ* orbital. Consequently, if the ligand backs away, it interacts less strongly with the dz2, and the dz2 falls slightly in energy. In general, orbital interactions obey conservation of energy, so if the dz2 drops in energy, then the dx2-y2 rises in energy.
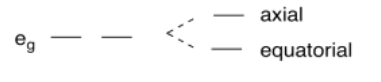
So, why does it have anything to do with an uneven distribution of electrons? In the case of Cu(II), which is d9, there are two electrons in one eg orbital and one in the other. If one of the orbitals goes down in energy and the other goes up, there may be no overall change in the energy of the orbitals, but there is a net decrease in electronic energy because two electrons are going down and only one is going up.
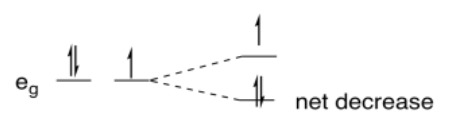
In comparison, if the metal were d10, two electrons would go down in energy and two would go up. There would be no overall change in energy and no advantage in undergoing a distortion.
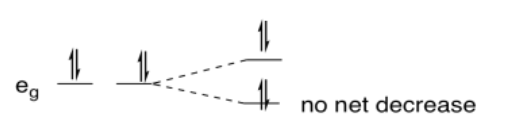
Would there be an advantage in undergoing a distortion in the following cases?
- low spin d7
- low spin d8
- Answer a
-
yes; low spin (ls) d7 is eg1, so one level has one electron and the other has none - net decrease in energy upon distortion
- Answer b
-
no; d8 is eg2, so both levels have one electron - no net change in energy upon distortion
In which of the following ions would you expect to see a Jahn-Teller distortion?
- Co(OH2)62+
- Ag(OH2)62+
- Ni(OH2)62+
- Mn(OH2)62+
- Ag(OH2)6+
- Answer
- Answer a
-
Co2+ yes; d7 so eg1
- Answer b
-
Ag2+ yes; d9 so eg3
- Answer c
-
Ni2+ no; d8 so eg2
- Answer d
-
Mn2+ no if hs; d5 so eg2. However, if it were low-spin (unlikely with a first-row metal in a moderately low oxidation state and π-donors), then there would be degeneracy and distortion.
- Answer e
-
Ag+ no; d10 so eg4
Similar distortions occur when there is degeneracy in the lower, t2g level. However, the distortions are more subtle because the d orbitals in this level interact much less strongly with the ligands. For example, it has been shown that in the d1 hexacyano titanium complex, [Ti(CN)6]3-, the equatorial Ti-C bond lengths are 2.168 Å, whereas the axial bond lengths are 2.199 Å, a difference of about 13%.
In which of the following ions would you expect to see a Jahn-Teller distortion?
- [V(CN)6]3-
- [Cr(CN)6]3-
- [Mn(CN)6]3-
- [Fe(CN)6]3-
- [Cr(CN)6]4-
- [Mn(CN)6]4-
- [Fe(CN)6]4-
- Answer
- Answer a
-
[V(CN)6]3- yes d2 t2g2
- Answer b
-
[Cr(CN)6]3- no d3 t2g3
- Answer c
-
[Mn(CN)6]3- yes d4 t2g4
- Answer d
-
[Fe(CN)6]3- yes d5 t2g5
- Answer e
-
[Cr(CN)6]4- yes d4 t2g4
- Answer f
-
[Mn(CN)6]4- yes d5 t2g5
- Answer g
-
[Fe(CN)6]4- no d6 t2g6
Although we have looked at a distortion via elongation of the axial pair of ligands, we could also get a complementary case in which the octahedron is compressed along one axis and stretched along the equatorial plane. However, the reasons for such a distortion are much the same as the one we looked at.
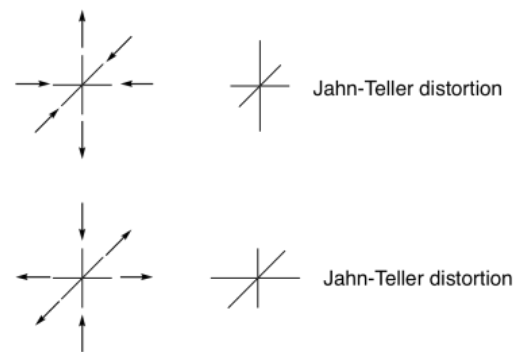
In practice, both distortions are possible, and it's difficult to predict which one will actually occur.
- Structural data for (bpy)Cu(II)(hfacac)2 from: Veidis, M. V.; Schreiber, G. H.; Gough, T. E.; Palenik, G. J. J. Am. Chem. Soc., 1969, 91 (7), 1859–1860.
- Computational data for the [Ti(CN)6]3- ion from: Atanasov, M.; Comba, P.; Daul, C. A.; Hauser, A. J. Phys. Chem. A, 2007, 111 (37), 9145–9163.


