2.10: Spectrochemical Series
- Page ID
- 195642
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Another factor that plays a key role in whether a transition metal complex is high- or low-spin is the nature of the ligands. The d orbital energy splitting is influenced by how strongly the ligand interacts with the metal. Ligands that interact only weakly produce little change in the d orbital energy levels, whereas ligands that interact strongly produce a larger change in d orbital energy levels.
The spectrochemical series is a list of ligands based on the strength of their interaction with metal ions. It is often listed, from weaker to stronger ligands, something like this:
I− < Br− < S2− < SCN− < Cl− < NO3− < N3− < F− < OH− < C2O42− < H2O < NCS− < CH3CN < py < NH3 < en < bipy < phen < NO2− < PPh3 < CN− < CO
in which py = pyridine; en = ethylenediamine; bipy = 2,2'-bipyridine; phen = 1,10-phenanthroline; SCN means the ligand is bound via sulfur and NCS via nitrogen.
The list can vary from one metal ion to another, since some ligands bind preferentially to certain metals (as seen in hard and soft acid and base chemistry).
What empirical trends can you see within the spectrochemical series? Are there any factors that make something a stronger field ligand?
- Answer
-
The weaker donors include halides and oxygen donors. Nitrogen atom donors are mostly a little stronger than that. The strongest donors include carbon donors, especially with pi bonds.
The d orbitals that rise in energy in the presence of a ligand can be thought of as forming an antibonding molecular orbital combination with an orbital on the ligand. In addition, there would also be a bonding combination for this interaction. That bonding orbital would be more like the initial ligand orbital. This premise is based on the idea that a ligand orbital is initially lower in energy than the metal orbital, so a bonding combination between these two orbitals is more like the initial ligand orbital, both in energy and location. The d orbital is initially higher in energy than the ligand orbital, so an antibonding combination between these two orbitals is more like the initial d orbital, both in energy and location.
- When orbitals on two different kinds of atoms combine, the antibonding orbital is considered to be more like the orbital that was initially at higher energy.
- In this case, it is still close to a d orbital in energy, location, and shape.
- When orbitals on two different kinds of atoms combine, the bonding orbital is considered to be more like the orbital that was initially at lower energy.
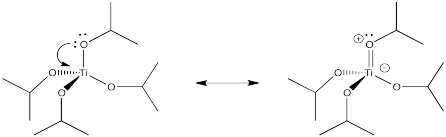
Suppose a ligand has more than one lone pair on the donor atom. The donor atom could share an extra pair of electrons with the metal, to form a double bond. This type of interaction is called pi-donation, because a pi bond is formed (not to be confused with sigma donation from a pi bond, as in alkene binding). Show an example using Ti(OiPr)4.
- Answer
-
In an octahedral environment, three of the d orbitals were not affected by sigma donation from the ligands. Show what happens to the energy level of these d orbitals in the presence of a pi donor.
- Answer
-
Pi donation raises the t2g electrons (the d electrons of proper symmetry for pi overlap with the ligands in an octahedral geometry).
Some ligands can accept a pair of electrons from the metal. An example is a carbonyl complex, which has a C=O pi antibonding orbital that can interact with a d orbital.
- Show the antibonding orbital on the carbonyl (CO) ligand.
- Show how a metal d orbital can interact with this orbital.
In the previous problem, a lower-energy atomic orbital on the metal interacts with a higher-energy antibonding orbital on the ligand. Show what happens to the energies of these two orbitals when they interact with each other.
- Answer
-
Add texts here. Do not delete this text first.
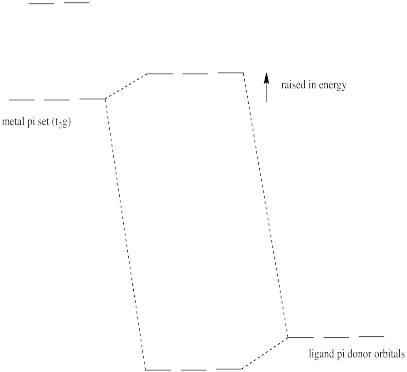
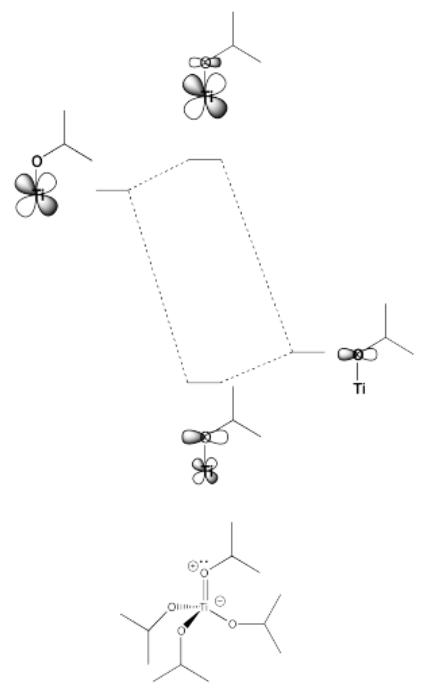
Some of the trends we see in the spectrochemical series arise from pi-donating and pi-accepting effects in the ligand. Ligands that have additional lone pairs (other than the one hat sigma donates) are pi donors. Pi donors raise the otherwise non-bonding t2g orbitals, because the lone pair on the ligand forms a pi bond with the metal. The t2g orbitals and the ligand lone pair orbitals form two new orbitals. The antibonding orbital is closer in energy to the high-energy d orbitals. The bonding orbital is closer in energy to the low-energy ligand orbital.
- Pi donation raises the t2g set of d orbitals in energy.
- As a result, the d orbital splitting gets smaller.
- Also as a result, a complex with pi donation is a little less stable than a complex without pi donation.
This type of interaction can be seen in the following pictures (a tetrahedral case).
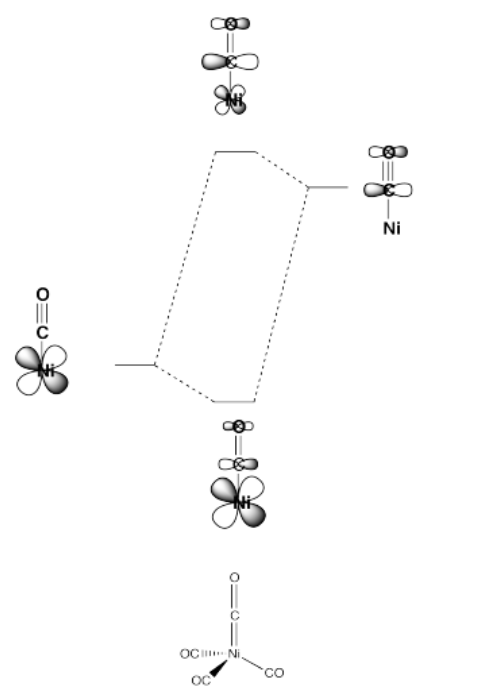
On the other hand, ligands in which the donor atom is already pi bonding to another atom can accept pi donation from the metal. This happens by donating an electron pair from a metal t2g orbital into a pi* orbital on the ligand. In this case, because the pi* is an antibonding orbital, it is higher in energy than the metal d orbital (or the t2g orbital). The resulting bonding orbital is more like the lower energy metal orbital, whereas the resulting antibonding orbital is more like the higher energy pi* orbital on the ligand.
- Pi accepting ligands lower the t2g set of d orbitals in energy.
- As a result, the d orbital splitting gets larger.
- Also as a result, a complex with a pi accepting ligand is a little more stable than a complex without a pi accepting ligand.
This type of interaction can be seen in the following case (a tetrahedral complex).
The spectrochemical series gets its name because of a shift in a band of the UV-Vis spectrum when two similar complexes are compared that have two different ligands. The effect of the ligand on the d orbital splitting has an effect on the wavelength of light associated with a d orbital (filled) to d orbital (empty) electronic transition. This transition is actually not associated with a major absorption by the compound; d orbital transitions are actually not that efficient at absorbing light. However, because they often occur in the region of visible light, they often lead to colored transition metal complexes.
The visible region includes photons with wavelengths from approximately 400 to 700 nm (really, a little bit lower and a little bit higher, but we are rounding). Photons with shorter wavelengths are invisible; if they are only a little shorter than visible light they are ultraviolet. Beyond that, photons with very, very short wavelengths are X-rays and gamma rays. Photons with longer wavelengths are also invisible; the infrared region is beyond about 700 nm. Beyond the infrared are microwaves and radio waves.

When we observe an object, what we see is the light that bounces off the object. If all wavelengths of visible light bounces off the object, the object appears white. If all wavelengths of visible light is absorbed by the object, the object appears black. If very specific wavelengths of visible light are absorbed, we see the other wavelengths, but the actual color that we perceive is slightly complicated, because of the way that we sense light.
In simple cases, the color absorbed and the complementary color that we see can be displayed using a color wheel. The color wheel displays the "complementary colors". When we see one of these colors, the light that is getting absorbed is the opposite one in the color wheel.

So, if we see something that looks bright blue, that object is really absorbing mostly orange light. If something absorbs violet light, it appears to us to have a yellow color.
Explain what happens to the wavelength of light absorbed for the d-d transition when a chloride ligand on a metal complex is replaced with a hydroxide ligand.
- Answer
-
Because chloride is a weaker ligand than hydroxide, the d orbital splitting gets smaller. A d-d transition would involve less energy, so it would move to longer wavelength (red shift).
The [Cu(OH2)6]2+ ion appears blue-green, whereas the [Cu(NH3)2(OH2)4]2+ ion appears indigo-violet.
- What colors do each of these complexes absorb?
- Which complex absorbs the highest-energy photons?
- If this absorption is due to a d-d transition, which complex has a larger d-d gap?
- Which compound has stronger field ligands?
- Answer
- Answer a
-
The [Cu(OH2)6]2+ ion appears blue-green, so it absorbs a reddish orange, about 650 nm; whereas the [Cu(NH3)2(OH2)4]2+ ion appears indigo-violet, so it absorbs yellow, about 600 nm.
- Answer b
-
Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon). The [Cu(NH3)2(OH2)4]2+ ion absorbs the shorter wavelength, higher energy photon.
- Answer c
-
The [Cu(NH3)2(OH2)4]2+ ion has the greater d-d gap.
- Answer d
-
The ammonia must be a stronger field ligand than water. In general terms we might think of that as a result of ammonia being only a sigma-donor, whereas water is also a pi-donor.
The [Cr(NH3)6]3+ ion appears yellow, whereas the [Cr(NH3)5Cl]2+ ion appears pink.
- What colors do each of these complexes absorb?
- Which complex absorbs the highest-energy photons?
- If this absorption is due to a d-d transition, which complex has a larger d-d gap?
- Which compound has stronger field ligands?
- Answer
- Answer a
-
The [Cu(NH3)6]3+ ion appears yellow, so it absorbs violet, about 400 nm; whereas the [Cu(NH3)5Cl]2+ ion appears pink, so it absorbs green, about 550 nm.
- Answer b
-
Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon). The [Cu(NH3)6]3+ ion absorbs the shorter wavelength, higher energy photon.
- Answer c
-
The [Cu(NH3)6]3+ ion has the greater d-d gap.
- Answer d
-
The ammonia must be a stronger field ligand than chloride. In general terms we might think of that as a result of ammonia being only a sigma-donor, whereas chloride is also a pi-donor.
A TA is preparing some cobalt samples for lab: one contains [Cr(OH2)6]3+, one contains [Cr(CN)6]3-, and one contains [CrF6]3-. Unfortunately, he gets them mixed up. He just has a beaker with green powder, a beaker with yellow powder, and a beaker with violet powder. Can you help him decide which is which?
- Answer
-
The green compound absorbs red; the violet compound absorbs yellow; the yellow compound absorbs violet.
In terms of energy these absorbances can be ranked:
(high energy) violet photon > yellow photon > red photon (low energy)
or in terms of d-d gap:
large gap > middle gap > small gap
In the spectrochemical series, we would expect the order of corresponding ligands to be:
-CN > H2O > F-
The cyano compound absorbs violet and appears yellow; the aquo compound absorbs yellow and appears violet; the fluoro compound absords red and appears green.
The [V(OH2)6]3+ ion appears yellow, whereas the [V(OH2)6]2+ ion appears pink.
- What colors do each of these complexes absorb?
- Which complex absorbs the highest-energy photons?
- If this absorption is due to a d-d transition, which complex has a larger d-d gap?
- Both compounds contain the same ligands. Why does one have a larger gap?
- Answer
- Answer a
-
The [V(OH2)6]3+ ion appears yellow, so it absorbs violet, about 400 nm; whereas the [V(OH2)6]2+ ion appears pink, so it absorbs green, about 550 nm.
- Answer b
-
Shorter wavelength is higher energy, according to the Planck-Einstein relation: E = hc/λ (in which h = Planck's constant, c = speed of light, λ = wavelength of photon). The [V(OH2)6]3+ ion absorbs the shorter wavelength, higher energy photon.
- Answer c
-
The [V(OH2)6]3+ ion has the greater d-d gap.
- Answer d
-
One ion contains V3+, whereas the other ion contains V2+. As charge increases on an ion, electrons contract toward the nucleus. However, low-lying electrons, which are closer to the nucleus to begin with, are attracted even more than are high-lying electrons. Thus, as charge increases on the ion, the d-d splitting increases.
Predict whether each of these coordination complexes is low spin or high spin.
a) [Co(NH3)6]+3 b) [Fe(CN)6]-4 c) [CoF6]-4
d) [Rh(CN)6]-3 e) [V(OH2)6]+3 f) [Fe(py)6]+2
g) [MnCl6]-4 h) [Ru(NH3)6]+2
- Answer
- Answer a
-
[Co(NH3)6]+3
The metal is +3 suggesting a large Δ0
The ligands are sigma donors, so medium field ligands
The splitting energy is large thus low spin.
- Answer b
-
[Fe(CN)6]-4
The metal is first row, +2 suggesting intermediate Δ0
The ligands are pi acceptors, so strong field ligands
The splitting energy is large thus low spin.
- Answer c
-
[CoF6]-4
The metal is first row, +2 suggesting a large Δ0
The ligands are pi donors, so weak field ligands
The splitting energy is small thus high spin.
- Answer d
-
[Rh(CN)6]-3
The metal is 2nd row (4d) and +3 suggesting a large Δ0
The ligands are pi acceptors, so strong field ligands
The splitting energy is large thus low spin.
- Answer e
-
[V(OH2)6]+3
The complex is d2, so there is only one possible spin state.
- Answer f
-
[Fe(py)6]+2
The metal is first row, +2 suggesting intermediate Δ0
The ligands are pi acceptors, so strong field ligands
The splitting energy is large thus low spin.
- Answer g
-
[MnCl6]-4
The metal is first row, +2 suggesting intermediate Δ0
The ligands are pi donors, so weak field ligands
The splitting energy is large thus high spin.
- Answer h
-
[Ru(NH3)6]+2
The metal is 2nd row (4d) and +2 suggesting a large Δ0
The ligands are sigma donors, so medium field ligands
The splitting energy is large thus low spin.


