2.8: Ligand Field Theory
- Page ID
- 195640
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Concepts from molecular orbital theory are useful in understanding the reactivity of coordination compounds. One of the basic ways of applying MO concepts to coordination chemistry is in Ligand Field Theory. Ligand Field Theory looks at the effect of donor atoms on the energy of d orbitals in the metal complex.
There are two ways in which we sometimes think about the effect of ligands on the d electrons on a metal. On the basis of simple electron-electron repulsion, donation of a lone pair might raise an occupied d orbital in energy. Alternatively, we can think about bonding interactions between ligand orbitals and d orbitals. This second way of thinking about things is a little bit more useful, and that's the approach we'll focus on, here.
Either way, there are interactions between ligand electrons and d electrons, that usually end up raising the d electrons in energy. The effect depends on the coordination geometry of the ligands. Ligands in a tetrahedral coordination sphere will have a different effect than ligands in an octahedral coordination sphere, because they will interact with the different d orbitals in different ways.
Ligand Field Theory looks at the effect of donor atoms on the energy of d orbitals in the metal complex. The effect depends on the coordination geometry geometry of the ligands.
Octahedral case
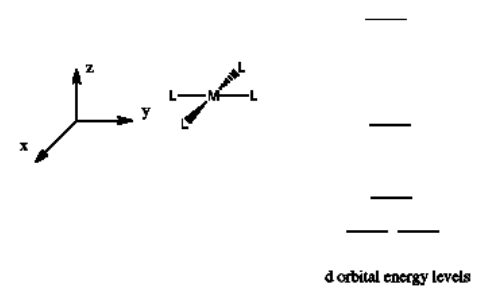
Suppose a complex has an octahedral coordination sphere. Assume the six ligands all lie along the x, y and z axes.
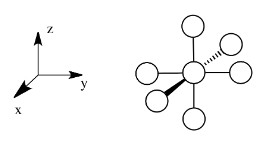
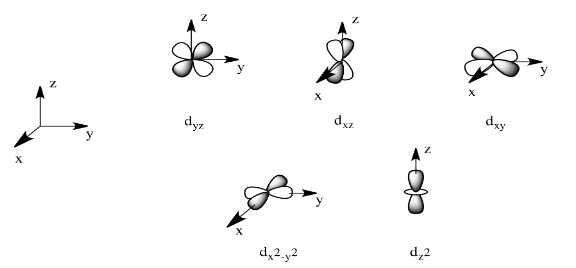
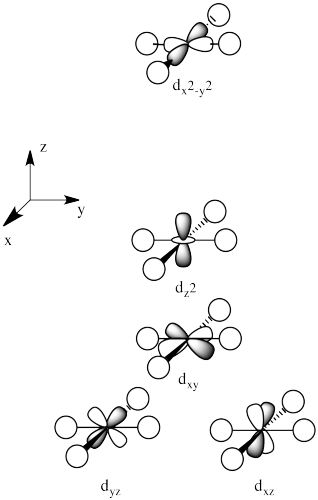
There are two d orbitals that will interact very strongly with these ligands: the dx2-y2, which lies directly on the x and y axes, and the dz2, which lies directly on the z axis. Together, these two metal orbitals and the ligand orbitals that interact with them will form new bonding and antibonding molecular orbitals.
The drawing below is simplified. The ligands will also interact with s and p orbitals, but for the moment we're not going to worry about them. We also won't worry about interactions from the other four ligands with the d orbitals (possible by symmetry considerations, but also a more complicated picture).
Now, remember that metals usually have d electrons that are much higher in energy than those on typical donor atoms (like oxygen, sulfur, nitrogen or phosphorus). That means the antibonding combinations will be much closer in energy to the original d orbitals, because both are relatively high in energy. The bonding combination will be much closer in energy to the original ligand orbitals, because these ones are all relatively low in energy.
That energetic similarity generally translates into a similarity in shape and location as well. In other words, the antibonding combination between a d orbital and a ligand orbital is a lot like the original d orbital. The bonding combination is more like the original ligand orbital than the original d orbital. Because of those similarities, inorganic chemists often refer to those antibonding orbitals as if they were still the original d orbitals.
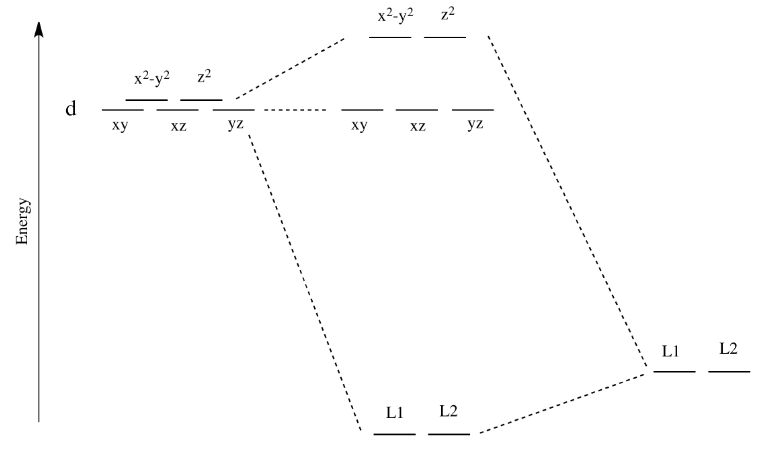
These two orbitals will be raised relatively high in energy by sigma bonding interactions with the donor orbitals. If there are electrons in the picture, it might look something like this:
- Assume the six ligands all lie along the x, y and z axes.
- The dx2-y2 and the dz2 orbitals lie along the bond axes.
- These two orbitals will be raised relatively high in energy.
- These orbitals are like antibonding levels.
- These orbitals are sometimes called the "eg" set of orbitals. The term "eg" comes from the mathematics of symmetry.
On the other hand, the other three d orbitals, the dxy, dxz and dyz, all lie between the donor ligands, rather than hitting them head-on. These orbitals will interact less strongly with the donor electrons.
- The dxy, dxz and dyz orbitals all lie between the bond axes.
- These three orbitals will be changed in energy only a little.
- These orbitals are more like non-bonding orbitals.
- These orbitals are sometimes called the "t2g" set of orbitals.
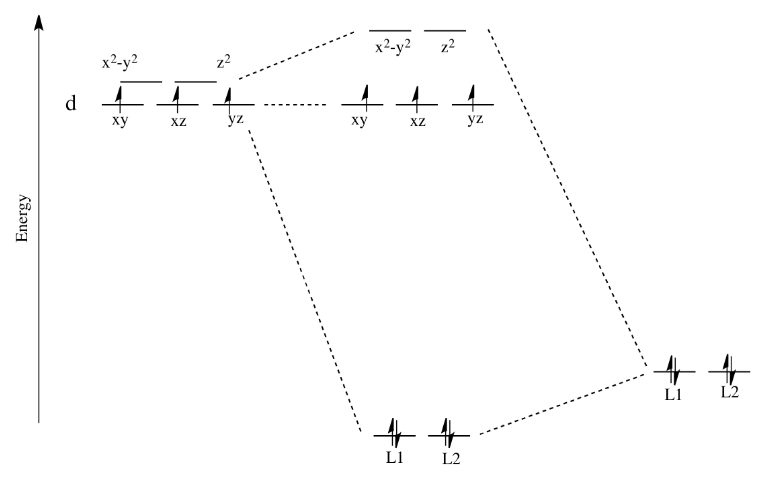
Remember, only the energy of the electrons affects the overall energy of the system. The unoccupied d orbitals are raised in energy, but the occupied orbitals go down in energy (or else stay the same).
Apart from the stabilization of the complex, there is another consequence of this picture. What we are left with is two distinct sets of d energy levels, one lower than the other. That will have an effect on the electron configuration at the metal atom in the complex. That means there will be cases where electrons could be paired or unpaired, depending on how these orbitals are occupied.
Take the case of the biologically important iron(II) ion. It has a d6 valence electron configuration. In less formal parlance of inorganic chemistry, "iron(II) is d6". In an iron(II) ion all alone in space, all the d-obitals would have the same energy level. We would put one electron in each orbital, and have one left. It would need to pair up in one of the d orbitals. (Notice that, in the chemistry of transition metal ions, the valence s and p orbitals are always assumed to be unoccupied).
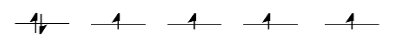
Things are very different in an octahedral complex, like K4[Fe(CN)6]. In that case, the d orbitals are no longer at the same energy level. There are two possible configurations to consider.
In one case, one electron would go into each of the lower energy d orbitals. A choice would be made for the fourth electron. Does it go into the higher energy d orbital, or does it pair up with one of the lower energy d electrons? The choice depends on how much higher in energy the upper d orbitals are, compared to how much energy it costs to put two electrons in the same d orbital.
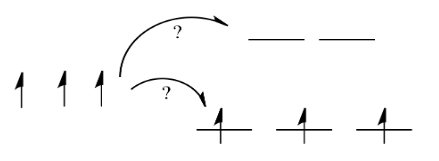
If the "d orbital splitting energy" is pretty low, so that the two sets of d orbitals are still pretty similar in energy, the next electron can go into a higher orbital. Pairing would not be required until the final electron. Overall, that would leave four unpaired electrons, just like in the case of a lone metal ion in space. This is called the "high-spin" case, because electrons can easily go into the higher orbital.
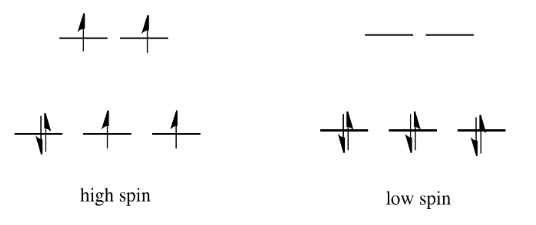
If the d orbital splitting energy is too high, the next electron must pair up in a lower orbital. All three remaining electrons pair up, and so there are no unpaired electrons in the complex. This is called the "low-spin" case, because electrons more easily pair up in the orbital.
So the overall rule is that if the energy to pair up the electrons is greater than the energy needed to get to the next level, the electron will go ahead and occupy the next level.
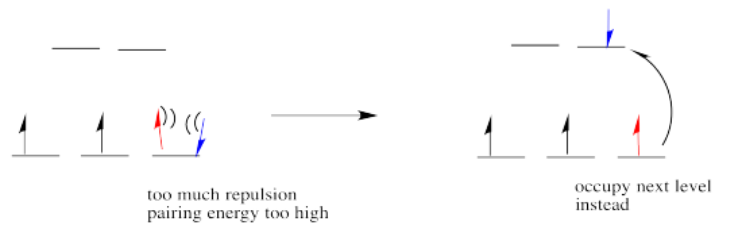
However, if the energy it takes to get to the next level is more than it would cost to pair up, the electrons will just pair up instead.
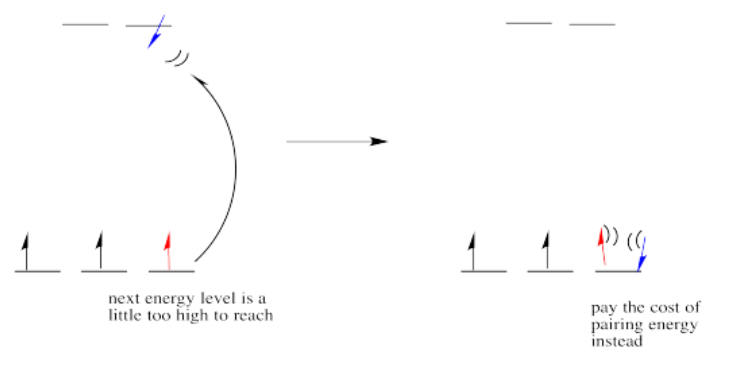
The electron configuration can be "high spin" or "low-spin", depending on how large the energy splitting is between the two sets of d orbitals.
The difference between the high-spin case and the low-spin case is significant, because unpaired electrons affect the magnetic properties of a material. The low-spin case would be diamagnetic, resulting in no interaction with a magnetic field. However, the high-spin case would be paramagnetic, and would be attracted to a magnetic field.
It turns out K4[Fe(CN)6] is diamagnetic. Thus, it is pretty clear that it is a low-spin complex. The energy difference between the two d orbital levels is relatively large in this case.
In addition to influencing magnetic properties, whether a complex is high- or low-spin also influences reactivity. Compounds with high-energy d electrons are generally more labile, meaning they let go of ligands more easily.
- electron configuration influences magnetic properties
- electron configuration influences lability (how easily ligands are released)
Reasons for Low-spin vs. High-spin: The Effect of the Metal Ion
There are a few factors that determine the magnitude of the d orbital splitting, and whether an electron can occupy the higher energy set of orbitals, rather than pairing up. It is based partly on ligand field strength, which is explored on the next page. It also depends on the charge on the metal ion, and whether the metal is in the first, second or third row of the transition metals.
The higher the charge on the metal, the greater the splitting between the d orbital energy levels. For example, Fe(II) is usually high spin. It has a smaller splitting between the lower and higher d orbital levels, so electrons can more easily go to the higher level rather than pair up un the lower level.
On the other hand, Fe(III) is usually low spin. It has a larger splitting between the d levels. In that case, it costs less energy for electrons to pair up in the lower level than to go up to the higher level.
- High-spin versus low-spin cases involve a trade-off between the d orbital splitting energy and the pairing energy.
- 2nd and 3rd row transition metals are usually low spin
- 1st row transition metals are often high spin
- However, 1st row transition metals and be low spin if they are very positive (usually 3+ or greater)
There is a lot going on in metal ions, but we'll take a simplified view of things. Thinking only about electrostatics, we can try to imagine what happens to those electrons when the charge on the metal ion changes.
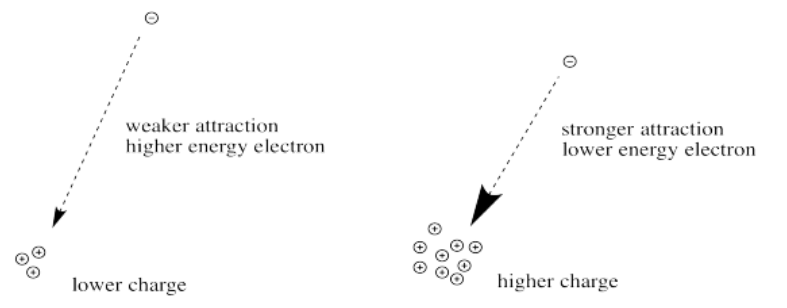
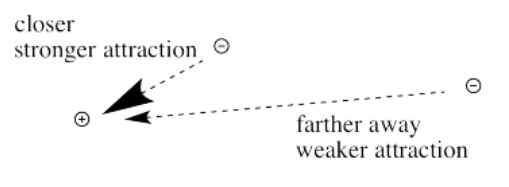
First we need to know about Coulomb's law. Coulomb's law states that the force of attraction between the electron and the nucleus depends on only two factors: the amount of positive charge in the nucleus, and the distance between the nucleus and the electron.
The greater the charge on the nucleus, the greater the attraction between the electron and the nucleus.
The farther an electron is from the nucleus, the weaker the attraction between the electron and the nucleus.
Coulomb's law can be used to evaluate the potential energy of the electron. It is one of the factors that determines how high or low those electronic energy levels are that we see in energy level diagrams for atoms, ions and molecules. The energy of the electron varies in a roughly similar way: the greater the charge on the nucleus, the lower the energy of the electron. Also, the closer the electron is to the nucleus, the lower its energy.
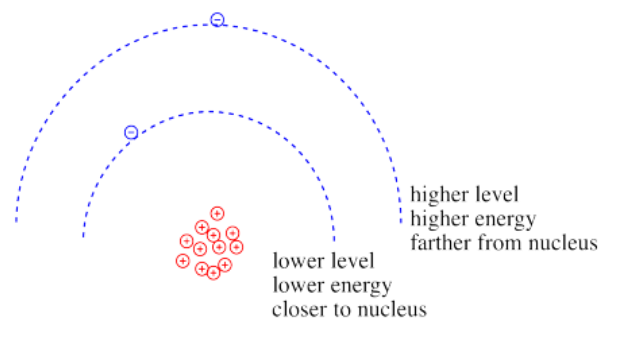
Roughly speaking, electrons at higher energy are farther from the nucleus. Electrons at lower energy are closer to the nucleus.
What happens if the charge increases? Maybe a lot more protons are added to the nucleus. Maybe some electrons are lost, so that to the remaining electrons it just feels like the charge of the nucleus has increased. Then the electrons should be more attracted to the nucleus. They get a little closer. Their potential energy drops.
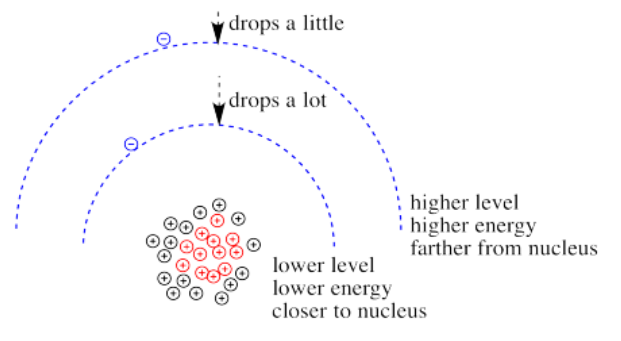
Of course, if one electron is closer to the nucleus already, it feels that increase in positive charge more strongly than an electron that is farther away. Consequently, it drops further in energy than an electron that is further away.
If we translate that idea into a picture of the d orbital energy levels in an octahedral geometry, it looks like this:
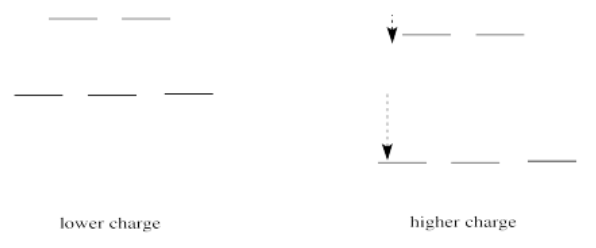
When the charge on the metal ion is increased, both the higher and the lower levels drop in energy. However, the lower level drops more. Thus, the gap between the levels gets wider.
Metals in the second and third row of the periodic table almost never form high-spin complexes. The d orbital energy splitting in these cases is larger than for first row metals. From a very simple point of view, these metals have many more protons in their nuclei than the first row transition metals, dropping that lower set of d electrons lower with respect to the higher set.
That isn't the whole picture for the second and third row transition metals, however. Remember, we are simplifying, and there are factors we won't go into. However, it is important to know that metal-ligand bond strengths are much greater in the second and third row than in the first. We'll look at the whole interaction diagram for an octahedral complex now, including contributions form metal s and p orbitals.
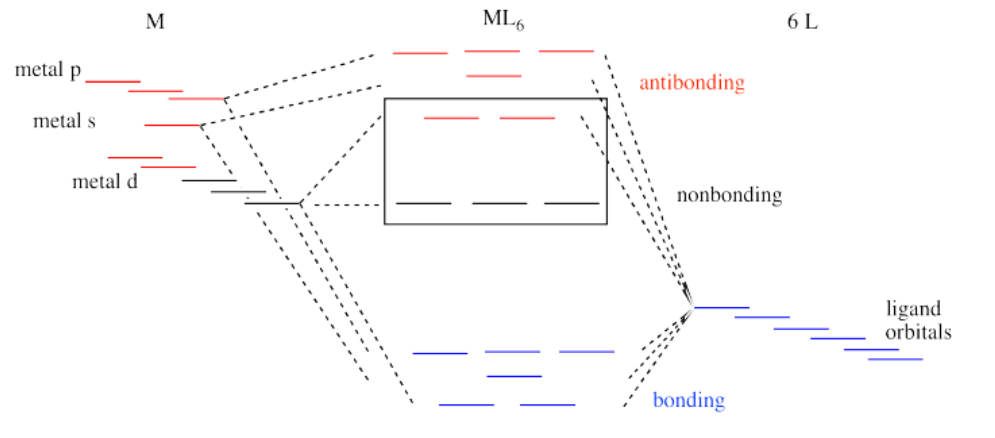
Like all ligand-metal interaction diagrams, the energy levels of the ligands by themselves are shown on one side. The metal's electronic energy levels are shown on the other side. The result of their interaction, a metal-ligand complex, is shown in the middle. The d orbital splitting diagram is shown in a box.
Suppose the diagram above is for a first row transition metal. The diagram for a second or third row metal is similar, but with stronger bonds.
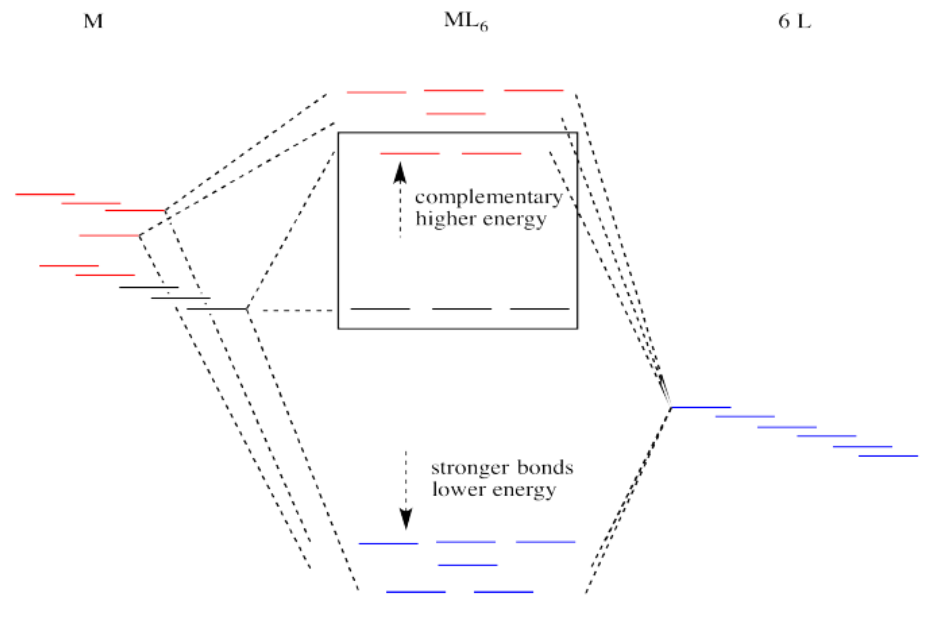
If the bonding interaction is stronger between the metal and ligand, then so is the antibonding interaction. The antibonding levels are bumped higher in energy as the bonding levels sink lower. Generally that's OK, because when the electrons are filled in, they will be found preferentially at the lower levels, not the higher ones. There will be a net lowering of electronic energy.
Why do second and third row transition metals form such strong bonds? Bond strengths are very complicated. In general, there is greater covalency between these metals and their ligands because of increased spatial and energetic overlap. Rather than go into those factors, we'll just think about all those extra protons in the nucleus that are attracting the ligand electrons more strongly.
There is one more important distinction that makes second and third row transition metals low spin. In addition, the pairing energy is lower in these metals because the orbitals are larger. There is more room for two electrons in one orbital, with less repulsion. As a result, electrons are much more likely to pair up than to occupy the next energy level.
- 2nd and 3rd row transition metals have stronger bonds, leading to a larger gap between d orbital levels
- 2nd and 3rd row transition metals have more diffuse orbitals, leading to a lower pairing energy
It is significant that most important transition metal ions in biology are from the first row of the transition block and are pretty labile. That fact plays an important role in the ease of formation and deconstruction of transition-metal containing proteins. In terms of formation, if the metal is more easily released by its previous ligands (either water or some compound that delivers the metal to the site of protein construction), it can form the necessary protein more quickly. However, even if a metal-containing enzyme plays a useful role, it should not be too stable, because we need to be able to regulate the level of protein concentration for optimum activity, or disassemble protein if it becomes damaged. Thus, it is important that the metal ion can be removed easily.
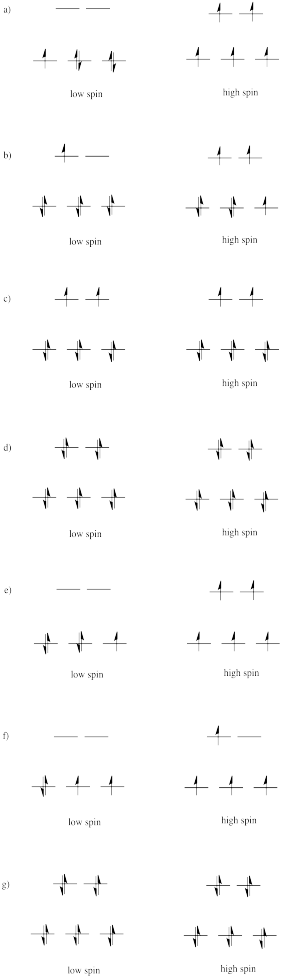
Draw both high spin and low spin d-orbital splitting diagrams for the following ions in an octahedral environment and determine the number of unpaired electrons in each case.
a) Mn2+ b) Co2+ c) Ni2+ d) Cu+ e) Fe3+ f) Cr2+ g) Zn2+
- Answer
-
The d orbital splitting diagram for a tetrahedral coordination environment is shown below. Given this diagram, and the axes in the accompanying picture, identify which d orbitals are found at which level. In the picture, the metal atom is at the center of the cube, and the circle represent the ligands.
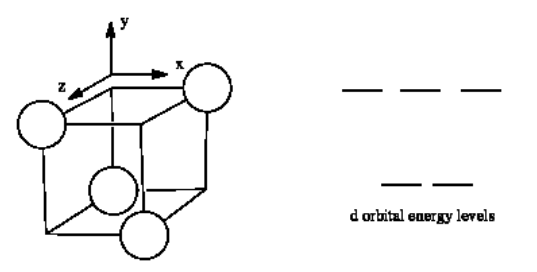
- Answer
-
The three orbitals shown above interact a little more strongly with the ligands. The three orbitals shown below interact a little more weakly.
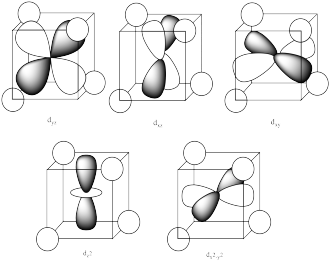
The reason for the difference in the interaction has to do with how close the nearest lobe of a d orbital comes to a ligand. There are really two possible positions: the face of a cube or the edge of a cube. If the ligands are at alternating corners of the cube, then the orbitals pointing at the edges are a little closer than those pointing at the faces of the cube.
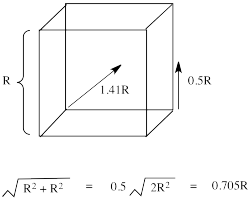
Typically, the d orbital splitting energy in the tetrahedral case is only about 4/9 as large as the splitting energy in the analogous octahedral case. Explain why it is smaller for the tetrahedral case.
- Answer
-
The ligands do not overlap with the d orbitals as well in tetrahedral complexes as they do in octahedral complexes. Thus, there is a weaker bonding interaction in the tetrahedral case. That means the antibonding orbital involving the d electrons is not raised as high in energy, so the splitting between the two d levels is smaller.
Suppose each of the ions in Exercise \(\PageIndex{1}\) (CC8.1) were in tetrahedral, rather than octahedral, coordination environments. Draw the d orbital diagrams for the high spin and the low spin case for each ion.
- Answer
-
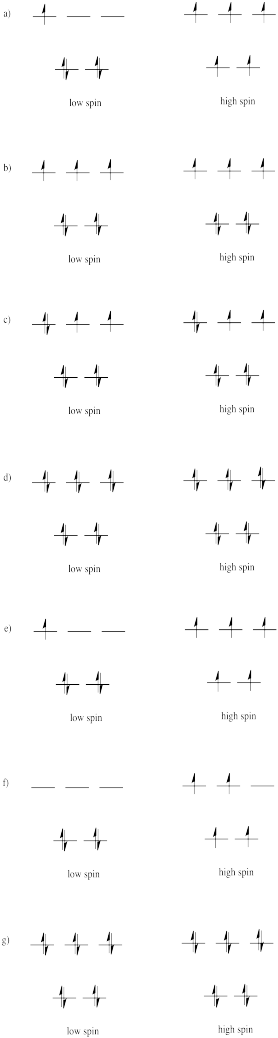
Usually, tetrahedral ions are high spin rather than low spin. Explain why.
- Answer
-
Because the d orbital splitting is much smaller in the tetrahedral case, it is likely that the energy required to pair two electrons in the same orbital will be greater than the energy required to promote an electron to the next energy level. In most cases, the complex will be high spin.
The d orbital splitting diagram for a square planar environment is shown below. Given this diagram, and the axes in the accompanying picture, identify which d orbitals are found at which level.
- Answer
-
The orbitals are shown in order of energy.
Predict whether each compound will be high or low spin.
- [Fe(py)6]2+
- [Fe(H2O)6]2+
- [FeBr6]3-
- [Co(NH3)6]3+
- [Cu(NH3)6]2+
- [Rh(CO)6]3+
- [Cr(CO)6]3+
- [PtCl6]2-
- Answer a
-
[Fe(py)6]2+ 3d metal, M+2, pi acceptor ligand → low spin
- Answer b
-
[Fe(H2O)6]2+ 3d metal, M+2, pi donor ligand → high spin
- Answer c
-
[FeBr6]3- 3d metal, M+3, pi donor ligand → high spin
- Answer d
-
[Co(NH3)6]3+ 3d metal, M+3, sigma donor ligand → low spin
- Answer e
-
[Cu(NH3)6]2+ 3d metal, M+2, sigma donor ligand → low spin
- Answer f
-
[Rh(CO)6]3+ 4d metal, M+3 → low spin
- Answer g
-
[Cr(CO)6]3+ 3d metal, M+3, pi acceptor ligand → low spin
- Answer h
-
[PtCl6]2- 5d metal, M+4 → low spin
Predict whether each compound will be square planar or tetrahedral.
- [Zn(NH3)4]2+
- [NiCl4]2+
- [Ni(CN)4]2-
- [Ir(CO)(OH)(PCy3)2]2+ ; Cy = cyclohexyl
- [Ag(dppb)2]+ ; dppb = 1,4-bis(diphenylphosphino)butane
- PtCl2(NH3)2
- PdCl2(NH3)2
- [CoCl4]2–
- Rh(PPh3)3Cl
- Answer a
-
[Zn(NH3)4] 2+ 3d metal, d10, sigma donor ligand → tetrahedral
- Answer b
-
[NiCl4] 2+ 3d metal, d8, pi donor ligand → tetrahedral
- Answer c
-
[Ni(CN)4] 2- 3d metal, d8, pi acceptor ligand → square planar
- Answer d
-
[Ir(CO)(OH)(PCy3)2] 2+ 5d metal, d8 → square planar
- Answer e
-
[Ag(dppb)2]1+ 4d metal, d10, sigma donor ligand → tetrahedral
- Answer f
-
[PtCl2(NH3)2] 5d metal, d8 → square planar
- Answer g
-
[PdCl2(NH3)2] 4d metal, d8, M+2, sigma donor ligand → square planar
- Answer h
-
[CoCl4] 2– 3d metal, d7, sigma donor ligand → tetrahedral
- Answer i
-
[Rh(PPh3)3Cl] 5d metal, d8 → square planar


