1.7: Equilibrium and pKa
- Page ID
- 195419
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Proton transfer reactions are very common. It's useful to be able to tell whether a proton is likely to be transferred from one position to another. Researchers have worked very hard to work out information that will give them some insight into that problem. The resulting data is often compiled into a pKa table, like the one below.
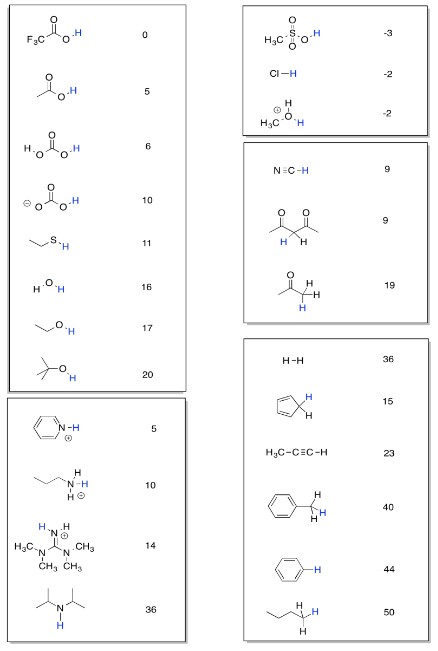
The table is organised into columns of compounds. On each compound, there is a hydrogen colored in blue. The pKa value listed next to the compound is an index of how tightly that hydrogen is held by the compound. The bigger the pKa, the more tightly that proton is held.
- A low pKa means the proton is given up easily. The compound is very acidic.
- A high pKa means the proton is held very tightly. The compound is not very acidic.
For example, methanesulfonic acid, CH3SO3H, is quite acidic. It has a low pKa. In this table, its approximate pKa is listed as -3. What does that mean exactly? Well, the equilibrium constant for the ionisation of any compound is 10-pKa. The equlibrium constant for the ionisation of methanesulfonic acid is 103, or 1000. That's the equilibrium constant for the reaction:
CH3SO2O-H = CH3SO2O- + H+
Of course, you may already know that a proton is not likely to wander around on its own. It is normally bound to a lone pair. In some studies, the lone pair is on a water molecule. Then the reaction would really look like this:
CH3SO2O-H + H2O = CH3SO2O- + H3O+
In other studies, the lone pair is on another solvent molecule, such as DMSO, (CH3)2SO. Then the reaction would really look like this:
CH3SO2O-H + (CH3)2SO = CH3SO2O- + (CH3)2SOH+
The actual value of the pKa varies depending on the conditions of the measurement. For example, a pKa measured in water is a little different from a pKa measured in DMSO, but the trends are generally the same.
We can use the pKa table to compare the acidity of different compounds. Methanesulfonic acid is much, much more acidic than butane, CH3CH2CH2CH3, which has a pKa of about 50. In addition, we can use the table to predict the direction of a reaction, or the equilibrium of a reaction. If a proton is being transferred from one position to another, a comparison of pKa values will tell us whether the reaction will proceed or not.
For example, consider the transfer of a proton from ethane thiol, CH3CH2SH, to pyridine, C5H5N (it looks like a benzene with one carbon replaced by a nitrogen). The pKa of the ethane thiol is 11. If the pyridine accepts the proton, it will form a pyridinium ion, C5H5NH+, with a pKa of 5. Qualitatively, we can already predict that the reaction will not proceed that well. The ethane thiol has a higher pKa than the pyridinium ion, so it will keep its proton, not give it away. However, the difference between the numbers isn't that large. Maybe there will be a measurable equilibrium, meaning an equilibrium in which there are measurable amounts of both products and reactants.
It can be shown that the equilibrium constant for a proton transfer reaction is K = 10(pKa2-pKa1), in which pKa2 is the pKa of the acid on the product side and pKa1 is the pKa of the acid on the reactant side. The acid is simply the species on either side that might give up its proton.
In this case,
K = 10(5-11) = 10-6.
The equilibrium constant is really defined as the ratio of the product concentrations to the reactant concentrations.
\[K = \frac{[products]}{[reactants]} \nonumber\]
K = [products]/[reactants]
In this case,
\[K= \frac{[CH_{3}CH_{2}S^{-}][C_{5}H_{5}NH^{+}]}{[CH_{3}CH_{2}SH][C_{5}H_{5}N]} \nonumber\]
We have two numbers multiplied together in the numerator and two numbers multiplied together in the denominator. Each time an ethane thiol and a pyridine react together and transfer a proton, we will get a thiolate anion and a pyridinium cation. In a simple case, we can think of an equal number of thiolate anions and pyridinium cations forming (since the same proton went from one to the other).
Then the equilibrium constant has a slightly simpler form:
\[K= \frac{x^{2}}{y^{2}} \nonumber\]
in which x = the concentration of either the thiolate or the pyridinium and y = the concentration of either the thiol or the pyridine.
In that case, the ratio of products to reactants, x/y, is equal to the square root of the equilibrium constant. In this case, the ratio is the square root of 0.000001. So the ratio of the products to the reactants is 0.001.
a) Predict the equilibrium constant for the reaction of pentane-2,4-dione, CH3COCH2COCH3, with sodium tert-butoxide, NaOC(CH3)3.
- Answer
-
K = 1020-9 = 1011
The table can often be used even if you don't see the compound you are looking for. Often, you can see something that looks pretty similar to what you are interested in and you can estimate the pKa that you need.
a) Predict the equilibrium constant for the reaction of 2-pentanone, CH3CH2COCH2CH3, with sodium methoxide, NaOCH3.
- Answer
-
K = 1017-19 = 10-2
Note that this pKa table is organised so that similar sorts of structures are placed in a box together. That arrangement is supposed to make it easier for you to look for trends and understand what kinds of factors make a proton more tightly held or more easily released.
- Compare a pair of compounds in the box of nitrogen compounds and explain why one has a higher pKa than the other.
- Compare a pair of compounds in the box of hydrocarbons and explain why one has a higher pKa than the other.
- Compare a pair of compounds in the box of O-H containing compounds and explain why one has a higher pKa than the other.


