10.3: Silicates and Silica

About 90% of the earth's crust is composed of silicate minerals. Silicates are compounds composed of silicon and oxygen; these compounds have negative charges on them. That means there are positive counterions found together with these anions. The variety of possible cations, ranging from sodium and potassium to copper and iron, is one of the factors that leads to a dazzling array of silicate minerals.

In addition to having a wide range of possible cations, silicate anions themselves have a breadth of available structures. These structures range from individual silicate anions (SiO₄^4-) to three dimensional networks of tetrahedra.

Silicates are not necessarily network solids, but we will see that their structures range from straightforward ionic solids at one extreme to something that looks more and more like an extended network at the other. By looking at these materials we can learn a little bit more about the related network solids.

Nesosilicates

Nesosilicates (meaning "island" silicates) are individual silicate anions arranged in crystalline ionic solids with their counterions. Those individual ions mean that nesosilicates are not network solids at all. They represent the extreme, other end of the silicate spectrum of structures.

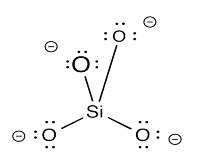
The nesosilicate anion forms a tetrahedral shape. The silicon atom is at the center and the oxygen atoms are at the four corners. That tetrahedral shape is often illustrated in structural drawings rather than drawing the atoms explicitly. Instead of showing the SiO₄^4- anion with labelled atoms on the left, the tetrahedron on the right is shown to represent it.

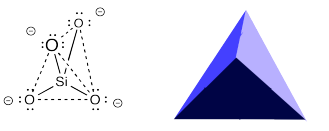
Silicates can have lots of different cations. Frequently, several different cations may be found in one material. For example, olivine is a pretty common nesosilicate with magnesium and iron cations (Mg²⁺ and Fe²⁺). If the olivine is of very high quality, it can be a gemstone, called peridot.

There are two limiting forms of olivine, called "endmembers". At one end is forsterite, Mg₂SiO₄. At the other end is fayalite, Fe₂SiO₄. In between is every possible combination of magnesium and iron. There could be equal amounts of magnesium and iron, or there could be just a few magnesium ions and many, many iron ions in a sample.

• Minerals frequently occur in families, in which one, similar ion can be substituted for another.
• Frequently, both ions can be present in varying amounts, but the properties of the material (such as color) change with changing ratios of these ions.
• The minerals that have just one of the possible ions but not the other are called the endmembers of the family.

Another common nesosilicate is garnet. Garnets are used as gems as well as abrasives -- they are sometimes used in sandpaper. There are many kinds of garnet, but a common one is almandine, the red-brown color of which we usually think of as "garnet". Garnets always contain two different cations. One of them is a M²⁺ ion and the other is a M³⁺ ion (M here just stands for "metal"). These two counterions are always present in a 3:2 ratio in garnet.

Exercise \(\PageIndex{1}\)

Show that forsterite and fayalite are overall neutral.

Answer a:

forsterite: Mg₂SiO₄: If each nesosilicate unit has a charge of 4^- because of the formal charges on the four oxygens, then the two magnesiums must combine to balance that charge with a 4⁺ charge. Each magnesium must have a 2⁺ charge of its own. That seems reasonable, since magnesium is two atoms from the left edge of the periodic table; it would have a 2⁺ charge in a noble gas configuration.

Answer b:

fayalite: Fe₂SiO₄: In order for this to work, each iron would have to have a 2⁺ charge. Transition metal charges are harder to predict than alkali and alkaline earth metals because they are farther from the edge of the periodic table, but it turns out that the two most common charges on an iron ion are 2⁺ and 3⁺, so this charge seems reasonable.

Exercise \(\PageIndex{2}\)

Suppose an olivine has 100 nesosilicate anions for every 25 magnesium ions.

1. How many iron ions (assume Fe³⁺) would there be in the neutral olivine?
2. What would be the values of x and y in Mg_xFe_ySiO₄?

Answer a:

If each nesosilicate has a charge of 4^-, then the total negative charge is 100 x 4^- = 400^-. If there are 25 magnesium ions, each with a 2⁺ charge, the total positive charge is 25 x 2⁺ = 50⁺. That leaves a net negative charge of 400^- + 50⁺ = 350^-. The irons would balance that charge with an equal positive charge. The number of iron ions would be 350+/3+ = 150.

Answer b:

If we divide these ratios by 100 to arrive at the one nesosilicate in the formula, we get Mg_0.25Fe_1.5SiO₄. It doesn't mean there is a quarter of a magnesium ion anywhere; this formula is just the overall ratio of atoms.

Exercise \(\PageIndex{3}\)

Almandine is a nesosilicate. It contains aluminum (which is almost always Al³⁺ in nature) and iron (in this case Fe²⁺) in a 2:3 ratio. What is its formula?

Answer

So far we have Al₂Fe₃. The positive charge = 2 x 3⁺ + 3 x 2⁺ = 12⁺. That charge must be balanced by the nesosilicate anions, which are each 4^-. So the number of silicates is 12^-/4^- = 3. The formula is Al₂Fe₃(SiO₄)₃.

Sorosilicates

Sorosilicates ("sister" silicates) are silicate anion dimers. The two silicate units share an oxygen atom. In the polyhedral depiction, the two tetrahedra share a corner. Sorosilicates clearly aren't network solids, either. They just contain slightly bigger anions than nesosilicates.

Sorosilicates are not nearly as common as nesosilicates. Where they exist, sorosilicates are found in the presence of other anions, as well as cations. In some minerals, they are even found in combination with nesosilicates. For example, epidote is a more common form of sorosilicate-containing mineral. It could be a number of colors but is usually green. It contains nesosilicate, sorosilicate, oxide and hydroxide anions, as well as calcium, iron and aluminum cations.

The sorosilicate anion can actually adopt different shapes in different cases. It contains two units that can twist relative to each other. The different shapes that result are called "conformations". A different conformation is shown below. In the picture on the left, we are looking at it from the same angle as the orosilicate shown above. In the picture on the right we are looking at it from a different angle to emphasize that the two tetrahedra are pointing in opposite directions. We are looking at the top of one tetrahedron but the bottom of the other one.

Exercise \(\PageIndex{4}\)

Epidote contains just one of each of its four different anions in its formula.

1. Write the formula, with appropriate charge, for each of its anions. Note that the oxygen atoms in the hydroxide (OH) and oxide (O) ions each have an octet.
2. Epidote also contains two Ca²⁺ ions in its formula, but varying amounts of Fe³⁺ and Al³⁺. How much iron and aluminum, total, does it have in its formula?

Answer a:

The anions are nesosilicate (4^-) + sorosilicate (6^-) + oxide (2^-) + hydroxide (1^-). The total charge is 13^-.

Answer b:

Calcium is an alkaline earth metal, two atoms from the left edge of the periodic table. The two calciums would partially balance that charge with 2 x 2⁺ = 4⁺ charge; the net charge is now 13^- + 4⁺ = 9^-.

If each Al or Fe has charge 3⁺, then the number needed to balance the charge is 9⁺/3⁺ = 3 Fe/Al ions.

Exercise \(\PageIndex{5}\)

Use your three-dimensional drawing tools (lines, wedges and dashes) to show the two different conformations of sorosilicate via Lewis structures.

Neither nesosilicates not sorosilicates are network solids. They are really just families of ionic solids. However, by looking at the relationship between the nesosilicate ion and the sorosilicate ion, we can see why many silicates do start to look more like network solids. If one oxygen atoms can be shared between two silicate units, maybe more can, too.

Inosilicates

If two silicate units can share an oxygen, more can, too. In fact, long chain silicates can form. To do so, two of the oxygens in a silicate unit have to be shared with two other silicate units. The same is true in the next unit, and so on, forming a long chain. Materials containing these long chain silicates are called inosilicates ("sinew" or "string" silicates). The polyhedral drawing of a section of inosilicate ion is shown below.

Inosilicates are not exactly network solids because they do not form three-dimensional networks. However, at least in one direction, they are covalently bonded and can extend indefinitely. There could be hundreds of silicate units in a row. In a sense, inosilicates could also be described as polymers. They contain individual units that keep repeating all along the chain. In the polyhedral drawing, the repeating units are simply tetrahedra.

The inosilicate chain drawn above does illustrate an important consideration that it has in common with network solids. All network solids are different on the inside than they are on the outside. We can illustrate that difference in the inosilicate chain because it is a relatively simple structure. In the inosilicate chain, each tetrahedron along the chain looks just like the next, but the ones on the end are different. They are only attached to one neighbor, not two. Compared to the other repeating units, these ones will have an extra oxygen with a negative charge.

Extending that idea to network solids, in which the covalent bonds extend in three directions, we will encounter a similar problem as we move out from the center of the solid and we reach the surface. The structure at the surface will be different from the structure in the interior of the solid, because we will run out atoms to keep connecting to.

• Network solids have different structures at the surface of the material than they do in the interior of the material.
• The surface of the material must have slightly different groups present because the network has come to an end.

One of the most important inosilicates is wollastonite, which is used in a number of industries. Wollastonite is a bright white mineral in which the counterion for the inosilicate is calcium ion, Ca²⁺. It is added to ceramic tiles, paints and plastics, partly because it increases their durability and strength. It is sometimes used to make brake pads for cars; it provides friction when pressed against the rotor, slowing down the wheels on your car, but because of its durability it does not wear out too quickly.

Exercise \(\PageIndex{6}\)

Convert the polyhedral drawing of inosilicate ion into a Lewis structure. You can stop after five repeating units.

Exercise \(\PageIndex{7}\)

Looking at the Lewis structure for inosilicate ion, how many calcium ions would accompany each repeating unit in Wollastonite?

Exercise \(\PageIndex{8}\)

In your Lewis structure for inosilicate ion, circle the repeat units. Propose a formula for Wollastonite.

Exercise \(\PageIndex{9}\)

Suggest a reason why Wollastonite might confer strength on ceramics and other materials.

Cyclosilicates

If silicate units can form chains, it shouldn't be a surprise that they can form other shapes, too. For example, the silicate units can wrap around to form rings. They come in a veriety of different sizes. These types of silicates are called cyclosilicates ("wheel" silicates).

On of the most familar cyclosilicate mineral groups is the beryl family. The most prominent member of the family is emerald. It contains the cyclic anion shown below.

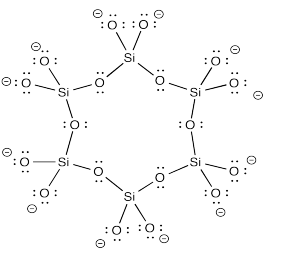
The polyhedral form is a gorgeous star.

All beryls have the same cyclosilicate anion. They even have the same counterions, with the general formula Be₃Al₂(Si₆O₁₈). However, beryls come in different colors because of small amounts of cation impurities. In emerald, a tiny amount of chromium ion provides the green color. In the closely related aquamarine, a tiny amount of Fe²⁺ results in a pale blue; however, when Fe³⁺ is present, the mineral is yellow, instead.

Exercise \(\PageIndex{10}\)

The California state gem, benitoite, contains a cyclosilicate anion with just three silicon atoms in it.

1. Draw the Lewis structure of this cyclosilicate.
2. Draw the polyhedral depiction of this cyclosilicate.
3. This anion is accompanied by a barium and a titanium ion. Given their places in the periodic table, what is the likely charge on each cation?

Clearly we have turned back from the edge of network solids again. These anions may be large, but they certainly don't extend on and on in any direction. However, previously, we looked at single unit silicates and extended them to doubles, then linked them together to make longer chains. What would happen if we could link some cyclosilicates together?

Instead of getting a one-dimensional chain, we would get a two-dimensional network.

Phyllosilicates

The name "phyllosilicates" means, roughly, "leaf"-silicates. These anions are sheets or leaves in which silicates link together to make two-dimensional networks. The structure shown below would extend on and on through the top, bottom and sides of the page (or the screen).

The most familiar examples of phyllosilicates are the mica family. If you have ever seen mica, with its thin sheets, you can easily imagine how it would be composed of two-dimensional networks like the one above. One of the most interesting applications of mica was its use as "Muscovy glass" in the old days in Russia. Its thin, transparent layers made very good windows.

Micas are a slightly more complicated example of phyllosilicates because they are also aluminosilicates. That is, they contain aluminum as well as silicon within their extended oxide network.

Another familiar example is chrysotile, which is one of many minerals that we think of as "asbestos". It is commonly called "white asbestos" and it accounts for the vast majority of asbestos mining in the world. Chrysotile has the formula Mg₃(Si₂O₅)(OH)₄.

Exercise \(\PageIndex{11}\)

Consider the formula for chrysotile.

1. What is the usual charge on a magnesium ion, given its place in the periodic table?
2. What is the charge on hydroxide ion?
3. The phyllosilicate ion is written as Si₂O₅, representing the overall ratio of those two atoms in the structure, but of course it does not come in units of that size. What is the total negative charge per Si₂O₅ unit?
4. What does that translate into in terms of negative charge per individual silicate unit (i.e. one individual silicate unit per silicon atom)? Explain whether that makes sense in terms of the polyhedral structure for a phyllosilicate shown above.

For decades, chrysotile was prized for its naturally insulating and fire-resistant qualities. It was commonly used in homes and other buildings until we realized that it produces a carcinogenic dust. Typically, the danger from this dust only arises from repeated exposure during the mining of asbestos and manufacture of asbestos-containing products. However, it could also be a long-term problem because of dust produced during building renovation projects.

Other, less common forms of asbestos include "blue asbestos" or crocidolite, with formula Na₂Fe^II₃Fe^III₂Si₈O₂₂(OH)₂, and grey-to-brown amosite, (Mg,Fe)₇Si₈O₂₂(OH)₂.

Note that there are some complications in the way these formulae are written. There are two different kinds of iron ion in crocidolite. One is an Fe²⁺ ion and the other is an Fe³⁺ ion. Often, in structures and formulae, the charges on metal ions are denoted by the "oxidation state", a number written using Roman numerals. Hence, Fe^II means Fe²⁺ in this context and Fe^III means Fe³⁺.

The formula for amosite is actually suggesting something that we have seen before. In amosite, iron and magnesium ions can easily replace each other in the structure. In this case, the ions are Mg²⁺ and Fe²⁺. The (Mg,Fe) just means we need some combination of these ions for a total of seven ions.

However, crocidolite and amosite are actually examples of inosilicates rather than phyllosilicates. They are a little bit different from the inosilicates that we saw before, however. Rather than containing single polysilicate chains, these materials contain double polysilicate ribbons.

In the picture, the inosilicate ribbon extends through the top and bottom of the page (or the screen) but not to the sides.

If you have ever seen asbestos, which is a fibrous mineral (a little like a clump of long hair), you may be able to imagine a connection between these structures and the physical appearance of the mineral.

Exercise \(\PageIndex{12}\)

Provide formulae for the endmembers of the amosite family.

Tectosilicates ("building" silicates) form three-dimensional frameworks.

In sorosilicates, individual silicate unit share oxygens with their neighbors via one of the corners of their tetrahedra. In inosilicates, individual silicate unit share oxygens with their neighbors via two of the corners of their tetrahedra. In phyllosilicates, individual silicate unit share oxygens with their neighbors via three of the corners of their tetrahedra.

In tectosilicates, individual silicate unit share oxygens with their neighbors via four of the corners of their tetrahedra.

These structures are pretty complicated and generally include aluminum as well as silicon oxides. However, an idealized drawing of such a network is shown below.

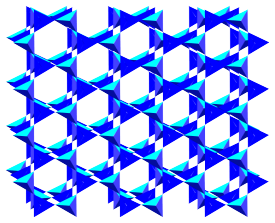
The idea of the drawing is that the silicate structure extends in two dimensions like the phyllosilicates, but also in a third direction, bonding to additional tetrahedra above and below the plane of the drawing.

Silica

Silica is truly a covalent network solid. Its formula is SiO₂. Unlike silicates, which are anions, it is a neutral compound, so it does not need counterions to balance a charge. Like the tectosilicates, it forms a three-dimensional network, with one individual silicate unit sharing an an oxygen with its neghbours via all four corners of the tetrahedron.

Although it is a three-dimensional extended solid, it is useful to look for sub-structures within the network, just as it is useful to identify unit cells of ionic solids. In silica, a pattern arises by following "chains" of silica tetrahedra through the network. As we follow along from one tetrahedron to the next, we find a spiral pattern in which each tetrahedron is twisted relative to the one before it. Eventually, every fourth (or in some cases, seventh) tetrahedron echoes the original and the pattern repeats itself.

This spiral shape is reminiscent of DNA. Like DNA, the chains within the three-dimensional structure form helices. They could form right-handed helices or left handed helices. As a result, silica is a "chiral" material and it is "optically active", topics that are covered in stereochemistry.

As in other network solids, silica must have a different structure on its surface than in the interior. On the surface, there are no more individual silicate units with which to form links.

Instead, dangling oxygen atoms may form covalent bonds to hydrogen, so that the surface is covered with OH groups. They may also remain as siloxide ions just as they do in silicates; in that case, they might have counterions such as sodium or potassium.

However, compared to the bulk interior of the solid, the surface contributes very little to the overall mass of the material. As a result, these extra hydrogens and sodiums are not included in the formula of silica. In reality, the true formula of a sample of silica might be something like this (just a fictional example to emphasize the idea):

\[\ce{Si1,022,000,000,000,000,000,000O2,044,000,000,000,000,000,000H36Na42} \nonumber\]

but nobody would ever write that. The material is one millionth of a percent hydrogen, one millionth of a percent sodium, about 66.7% oxygen and approximately 33.3% silicon. It's pretty darned close to SiO₂.

Silica is a very common material. Its most familiar pure form is quartz. In addition to being found as large crystals, microcrystalline particles of quartz is found in a wide rage of other minerals. It's also the major component of sand.

Exercise \(\PageIndex{13}\)

Zircon is a nesosilicate containing Zr⁴⁺ ion. What is its formula?

Exercise \(\PageIndex{14}\)

Propose a formula for a simple, single-chain inosite containing only sodium counterions.

Exercise \(\PageIndex{15}\)

Jadeite is beautiful green mineral; high quality stones are one of the forms of the gemstone, jade. Jadeite is a simple, single-chain inosite containing equal numbers of Na⁺ and Al³⁺ counterions. Propose a formula for this mineral.